Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

7.4. Mur en aile

Les murs en ailes sont des voiles de part et d'autre de la culée pour retenir les remblais derrière cette dernière. Il est soumis aux sollicitation suivantes :

? Horizontalement il est soumis à la poussée des terres et à la poussée due aux surcharges sur le remblai ;

? Verticalement il est soumis à son poids propre ;

7.4.1. Evaluation des charges

[105]

? Charges verticales :

? Poids des terres derrière le mur (P3) : P'3 = (1m+3,0m) x 2,0m x 1,8t/m³ x 1m = 14,4 t P»3 = (2m - 0,50m) x 2,0m x 2,60 t/m³ x 1m = 7,8 t P3 = P'3 + P»3 = 14,4 t + 7,8t = 22,2 t

Excentricité : x = (2,0m) + 0,80m + 1,20m = 2,67m ? Poids de la semelle (P2) :

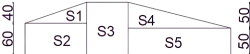
S1 = = 0,24 m² ; S2 = 0,60m x 1,20 = 0,72 m²

S3 = 0,80m x 1,00m = 0,80 m² ; S4 = = 0,50 m²

S5 = 0,50 x 2,0m = 1,0 m²

St = 0,24 m² + 0,72 m² + 0,80 m² + 0,50 m² + 1 m² = 3,26 m²

=

P2 = 3,26 m² x 2,5 t/m³ x 1m = 8,15 t

Excentricité: X1 = (1,20m) = 0,80m ;	X2 = (1,20m) =	0,60 m ; X3 =	(0,80m)	+ 1,20m
1,60 m ; X4 = (2,0m) + 0,80m + 1,20m	= 2,67 m ; X5 =	(2m)+ 0,80m	+ 1,20m	= 3,0m

?

X ?

= 1,913 m

? Poids du corps du Mur (P1) :

S = 0,80m x 5 m = 4 m² ; P1 = 4 m² x 2,5 t/m³ x 1m = 10 t

Excentricité : X = (0,80) + 1,20m = 1,60m ;

[106]

? Charges horizontales :

· Poussées des terres dues au poids du sol (H3^' et H3^») :

ü Pour le sable :

H'3 = ₂¹(?sable x h² x k) = ₂¹(1,8t/m³ x (4,0)² x 0,33) x 1m = 4,752 t

Excentricité : X= ¹(6,0 - 2,0) = 1,33m

ü Pour le sable limoneux :

Contrainte horizontale : óh = - v2 avec ó_v = (2,6 t/m³ x 2m ) = 5,20 t/m²

5,20 2(1)

óh _=2,46 - V2,46 = 0,838 ^t/m2H»3 = 1 (0,838 t/m² x 2m ) x 1m = 0,838 t 2

Excentricité : X= ¹(2m) = 0,67m

· Poussée de terres due à la surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m² x 6,0 m x 1m = 2,4 t Excentricité : X= ₂¹(6,0m) = 3,0m

^TABLEAU DES FORCES VERTICALES
^Charges verticales	^(t)	^Excentricit ^é (m)	^Moment ^stabilisant
^P1	^10	^1,6	^16
^P2	^CHARGES ^8,15	^1,913	^15,59095
^P3	^22,2	^2,67	^59,274
^SOMMES	^40,35		90,86495

[107]

^TABLEAU DES FORCES HORIZONTALES
^Charge horizontale	CHARGE(t)	^Excentricit ^é (m)	^Moment ^renversant
^H'3	^4,752	^1,33	^6,32016
^H"3	^0,838	^0,67	^0,56146
^H4	^2,4	^3	^7,2
^SOMMES	^7,99		^14,08162

7.4.2. Etude de la stabilité

v Stabilité au renversement : ? >1,5 ? > 1,5 ? 6,45 > 1, ; 5 la condition
? --

--

est vérifiée.

v Stabilité au glissement : E Fh > 1,5 ? 9 > 1,5 ? 5,050 > 1,5 ; la condition est vérifiée.

v Stabilité face aux contraintes transmise par le sol : Le calcul des contraintes se fera comme dans le cas de la culée. La culée travaille en flexion composée. D'où :

? ómax =

x (1 + ) et ómin = ? x (1 -

)

· Calcul de l'excentricité (e) : e = ' - x

? ?

or

= = 1,90 m

?

e = - 1,90m = 0,10 m

condition : 0 ? e = ? 0 ? 0,10 = ? 0 ? 0,10 = 0,67 condition vérifiée l'excentricité se trouve dans le noyau central.

· Vérification des contraintes :

ómax = x (1 + ) = 13,265 t/m²

ómin = x (1 - ) = 6,909 t/m2

[108]

ómax < ósol ^et ómin > 0 ? 13,265 t/m² < 22 t/m² et 6,909 t/m² > 0. Condition vérifiée ? Diagramme de contrainte :

^ómin = ^{6,909 t/m2}

^ómax = ^{13,265 t/m2}