Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

7.1. Appareils d'appuis

Nous utiliserons des appareils d'appuis fixes qui assurent l'immobilité de la section reposant sur eux et les rotations. Nous avons opté pour les appareils d'appuis en élastomères frettés ou néoprène qui a pour avantage :

· Une bonne résistance au cisaillement et à la traction ;

· Présente un pouvoir remarquable d'élasticité et d'allongement ;

· Très disponible sur le marché ;

Une plaque en néoprène est composée d'une tôle en acier et d'une couche d'élastomère(caoutchouc).

Fig.

Le calcul se fait en fonction des conditions suivantes :

· Vérification des contraintes à vide et sous charge ;

· La distorsion due à la variation de la température ;

· La distorsion due à l'effort de freinage ; ? Quelques spécifications techniques :

· Limite de contraintes à la compression :

- A vide : 95 bars (poids propre du tablier et la charge de la foule) - Sous charge : 135 bars (le trafic y compris)

[90]

· Variation de la température : ÄT = 10°C

· Coefficient thermique : X = 1,2 x 10^-5

· Module d'élasticité : E = 10 bars

v Pré-dimensionnement :

Nous optons pour une plaque de 10 mm c'est-à-dire 1mm pour la tôle en acier et 9mm pour l'élastomère (en caoutchouc) soit 1cm en tout.

v Vérification

ü A la compression :

On sait que :

· Tconvois = 29,241 t x 1,5 = 43,8615 t

· Tfoule = 8,33 t x 1,5 = 12,495 t

· Tpoids propre = 44,4679625 t x 1,35 = 60,03174 t

A vide : R1 = Tfoule + Tpoids propre = 72,52674 t = 72526,74 kg

< 95 bars ? < 95 kg/cm² ? < 95 kg/cm² ? S1 = 763,43cm²

Sous charge : R2 = Tconvois + _Tfoule + Tpoids propre = 116,38824 t = 116388,24 kg

,2

< 135 bars ? < 135 kg/cm2 ? < 135 kg/cm2 ? S2 = 862,1351cm²

Pour trouver la section d'appareil d'appuis nous prenons : Sappareil d'appuis ? Smax et

Smax = max (S1 ; S2) ? Smax = max (763,43cm² ; 862,1351cm²) ? Smax = 862,1351 cm², nous adoptons : Sappareils d'appuis = 900 cm²

Nous cherchons à déterminer la section (a x b) qui va résister à l'effort de freinage et l'épaisseur (e) qui va résister à la variation de la température.

ü A la distorsion :

Distorsion due à la variation de Température (d1) :

Ici : d1 < 0,5. e avec : d1 = X. ÄT. où L est la portée

d1 = 1,2 x 10^-5 x 10 x = 0,102cm ? 0,102cm < 0,5.e d'où e ? ? e ? 0,204 cm

nous adoptons : e = 12 cm

[91]

Distorsion due à l'effort de freinage (d2) :

Ici : d2 = avec F =

Alors : ? Effort de freinage =

=

x 1m = 4 t = 4000 kg

? Nombre de poutre : 4 ? Nombre d'appuis : 2

Avec E = 10 bar = 10 kg/cm² d'où F = = 500 kg

Ainsi : d2 = = 0,666 cm

? Condition : d1 + d2 ? 0,7 e

? 0,102 cm + 0,666 cm ? 0,7 x 12 cm ? 0,768 cm ? 8,4 cm d'où la condition est vérifiée.

7.2. Dalle de transition

Fig.

La dalle de transition est appuyée d'un côté par le mur garde grève (corbeau) et de l'autre côté sur le remblai (appuis élastique). Elle s'étant sur une longueur de 5m et a une largeur correspondant à celle du pont soit 12m.

CL = = = 0,4166 0,42 ? 0,40 ; la dalle porte dans deux sens.

? Evaluation des charges :

? Poids propre de la dalle : 0,25m x 2,5 t/m³ = 0,625 t/m2

[92]

· Poids de la chaussée :

· Revetement : 0,08m x 2,4 t/m³ = 0,192 t/m²

· Chape d'étanchéité : 0,04m x 2,1 t/m² = 0,084 t/m²

· Couche de forme : 0,04m x 2,2 t/m² = 0,088 t/m² Poids de la chaussée : PChaussée = 0,364 t/m²

· Surcharge sur remblais : 1 t/m2

· Convoi :

Les surfaces d'influences de la dalle seront données par :

> Sens de x :

S1 = L1 x L2

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,25m) + = 2,706 m

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,25m) = 1,04 m D'où S1 = 2,706 m x 1,04 m = 2,814 m2

Alors la densité sera : x õdalle = x 1,2 = 3,198 t/m²

> Sens de y :

S2 = L1 x L2

L2 = a2 + 1,5 h_r + 2 hd = 0,30m + 1,5 (0,16m) + 2 (0,25m) = 1,04 m

L1 = a1 + 1,5 h_r + 2 hd + = 0,30m + 1,5 (0,16m) + 2 (0,25m) + = 5,04 m

D'où S1 = 1,04 m x 5,04 m = 5,2416 m2

Alors la densité sera : x õdalle = x 1,2 = 1,717 t/m²

La charge du convoi est donc : Pconvois = 4,915 t/m²

Combinaisons des charges : PS = 0,625 t/m2 + 0,364 t/m2 + 1 t/m2 + 4,915 t/m2 = 7,268 t/m2

? Calcul des moments :

Par la méthode forfaitaire on a : pour á = 0,42 ; u_x = 0,1098 et u_y = 0,3000 ; l_x = 5m

[93]

Mox = ì_x. Ps. l_x² = 0,1098 x 7,268 t/m² x (5m)² = 19,951 tm Moy = ì_y. Mox = 0,3000 x 19,951 tm = 5,9853 tm

Suivant le petit côté X :

? Moment en travée :

Mtx = 0,85. Mox = 0,85 x 19,951 tm = 16,958 tm

? Moment aux appuis :

Max = - 0,5. Mox = - 0,5 x 19,951 tm = - 9,9755 tm

Suivant le grand côté Y :

? Moment en travée :

Mty = 0,85. Moy = 0,85 x 5,9853 tm = 5,0875 tm

? Moment aux appuis :

May = - 0,5. Mox = - 0,5 x 19,951 tm = - 9,9755 tm

7.3. Culée

Fig.

[94]

Les sollicitations sur la culée sont calculées par une tranche d'un mètre. Le bras de levier est pris par rapport au point O.

7.3.1. Evaluation des charges.

Fig.

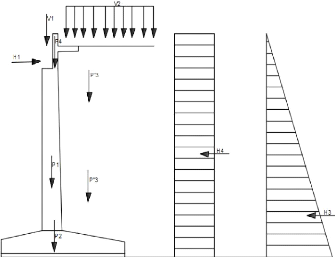
? Charges verticales :

? Poids des terres derrière le mur (P3) :

P'3 = (1m+3,0m) x 3,0m x 1,8t/m³ x 1m = 21,6 t

P»3 = (2m - 0,50m) x 3,0m x 2,60 t/m³ x 1m = 11,7 t P3 = P'3 + P»3 = 21,6 t + 11,7t = 33,3 t

Excentricité : x = ¹(3,0m) + 1m + 2,0m = 4,0m ? Poids de la semelle (P2) :

[95]

S1 = = 0,4 m² ; S2 = 0,60m x 2,0 = 1,2 m²

S3 = 1,00m x 1,00m = 1 m² ; S4 = = 0,75 m²

S5 = 0,50 x 3,0m = 1,50 m²

St = 0,4 m² + 1 m² + 1,50 m² + 1,2 m² + 0,75 m² = 4,85 m² P2 = 4,85 m² x 2,5 t/m³ x 1m = 12,125 t

Excentricité: X1 = (2,0m) = 1,33m ; X2 = (2,0m) = 1 m ; X3 = (1m) + 2,0m = 2,50 m ; X4 = (3,0m) + 1m + 2,0m = 4 m ; X5 = (3,0m)+ 1m + 2,0m = 4,5m

?

?

X

= 2,985 m

? Poids du corps de la culée(P1) :

S1 = 0,80m x 3,38 m = 2,704 m² ; S2 = = 0,338 m²

St = 2,704 m² + 0,338 m² = 3,042 m²

P1 = 3,042 m² x 2,5 t/m³ x 1m = 7,605 t

Excentricité : X1 = (0,80) + 2,0m = 2,40m ; X2 = (0,20) + 0,80m + 2,0m = 2,86m

?

?

X

= 2,451 m

? Poids du mur garde grève (P4) :

S1 = 0,30 m x 1,62m = 0,486 m² ; S2 = 1m x 0,25m = 0,25 m² St = 0,25 m² + 0,486 m² = 0,736 m²

P4 = 0,736 m² x 2,5 t/m³ x 1m = 1,84 t

Excentricité : X1 = (0,30m) + 0,50m+ 2,0m = 2,65 m ; X2 = (1m) + 0,30m + 0,50m + 2,0m = 3,30m

= 2,870 m

?

?

X

[96]

? La réaction verticale due à l'action des charges verticales (V1) : L'effort tranchant max(ELS) : Tmax = 82,0389625 t

Comme il y a 4 appuis sur la culée, on obtient :

V1 = x 1m = 27,346320 t

Excentricité : X= (0,50m) + 2,0m = 2,25m ? Poids de la surcharge(V2) : 1t/m²

V2 = x 1m = 1,95 t

Excentricité : x = (3,0m) + 1m + 2,0m = 4,0m

? Poids de la dalle de transition (V3) : P_s = 0,625t/m² + 0,364t/m² = 0,989 t/m² V3= 0,989 t/m² x 5m x 1m = 4,945 t

Excentricité : x = (3,0m) + 1m + 2,0m = 4,0m

? Charges horizontales :

Le coefficient des poussées des terres k est donné par :

Pour le sable : Nõ = tg²(45+ ) = tg²(45+ ) = 3 ; k = = = 0,33

Pour le sable limoneux : Nõ = tg²(45+ ) = tg²(45+ ) = 2,46 ; k = = = 0,40

Pour le calcul de l'effort de freinage et de la poussé due à la surcharge, nous utiliserons le

coefficient des poussées des terres le plus élevé soit k = 0,40 ? Effort de freinage (H1) :

H1 =

Avec : - k : coefficient des poussées des terres = 0,40

- N : nombre de bandes = 2

[97]

- C : convois : 60t

- lp : largeur du pont = 12 m

t

H1 = o,4ox2x6o x 1m = 4 t
12m

162m

Excentricité : X = 6,0 - , = 5,19 m

· Poussées des terres due au poids du sol (H3^' et H3^») :

ü Pour le sable :

H'3 = ₂¹(?sable x h² x k) = ₂¹(1,8t/m³ x (4,0)² x 0,33) x 1m = 4,752 t

Excentricité : X= ¹(6,0 - 2,0) = 1,33 m

ü Pour le sable limoneux :

cu

Contrainte horizontale : 6h = - 2 avec 6_v = (2,6 t/m³ x 2m ) = 5,20 t/m²
tpf tp

5,2 2(1)

6h _2,46 - 1/2,46 = 0,838 ^t/m2

H»3 = 1 (0,838 t/m² x 2m ) x 1m = 0,838 t

²

Excentricité : X= ¹(2m) = 0,67m

· Poussée de terres due à la surcharge (H4) : H4 = k x V2 x Hculée = 0,40 x 1t/m² x 6,0 m x 1m = 2,4 t Excentricité : X= ₂¹(6,0m) = 3,0m

[98]

^TABLEAU DES FORCES VERTICALES
^Charges verticales	^CHARGES (t)		^(m)		^Moment stabilisant ( ^tm)
^P1	^7,605		^2,451		^18,639855
^P2	^12,125		^2,985		^36,193125
^P3	^33,3		^4		^133,2
^P4	^1,84		^2,87		^5,2808
^V1	^27,34632		^2,25		^61,52922
^V2	^1,95		^4		^7,8
^V3	^6,675		^4		^26,7
^SOMMES	^90,84132				^289,343
^Excentricité ^TABLEAU DES FORCES HORIZONTALES
^Charge horizontale		CHARGE(t)		^(m)	^Moment renversant ^(tm)
^H1		^4		^5,19	^20,76
^H'3		^4,752		^1,33	^6,32016
^H"3		^0,838		^0,67	^0,56146
^H4		^2,4		^3	^7,2
^SOMMES		^11,99		^Excentricité	^34,84162

7.3.2. Etude de la stabilité

E Ms 289,343 Stabilité au renversement : > 1 5 ? >	1,5 ?	? 8,3 7,57 >	> 1,5 · la ' 1,5 ; la condition
E Mr - ' 34,84162 condition est vérifiée. Fi; 90,84132
v > > 1,5 Stabilité au glissement : Fh 1,5 ? 11,99

est vérifiée.

v Stabilité face aux contraintes transmise par le sol :

Condition : Emax ? Esol et Emin ? 0

Pour le choix du type de fondation, nous avons choisi les fondations directes (avec semelles) ; la profondeur du bon sol étant de 5m. La condition est que la contrainte admissible du sol support doit être d'au moins : Esol = R_p / 10 > 0,1 MPa

[99]

Notre sol présente une contrainte de rupture à la pointe minimum de 1,4 MPa ; alors la

contrainte admissible du sol sera : ósol = _ = 0,22 MPa > 0,1 MPa

La culée travaille en flexion composée. D'où :

? ?

ómax = X (1 + ) et ómin = x (1 - )

· Calcul de l'excentricité (e) : e = - x

=

or x=

? ?

?

= 2,80 m

e = - 2,80m = 0,20 m

condition : 0 ? e = ? 0 ? 0,20 = ? 0 ? 0,20 = 1. Condition vérifiée l'excentricité

se trouve dans le noyau central.

· Vérification des contraintes :

ómax = T x (1 + ) = 18,168 t/m²

ómin = x (1 - ) = 12,112 t/m²

ómax ? ósol et ómin > 0 ? 18,168 t/m² ? 22 t/m² et 12,112 t/m² > 0. Condition vérifiée

· Diagramme de contrainte :

^ómin = ^{12,112 t/m2}

^ómax = ^18,168 t/m2

[100]

7.3.3. Calcul proprement dit de la culée

Fig.

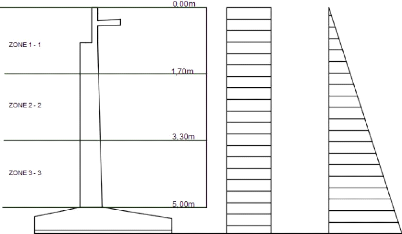
7.3.3.1. Calcul du corps de la culée et mur garde grève
7.3.3.1.1. Calcul des moments

? Effort de freinage

=

H1 = x 1m = 4 t ; alors H1' = H1» = H1''' ; c'est-à-dire que l'effort
de freinage reste ainsi dans chaque zones.

On trouve l'excentricité dans chaque zones : x = Hi-i

x1 = 0,89m ; x2 = 2,49m ; x3 = 4,19m

? Poussée due à la surcharge

H2 = k x V2 x H2-2

1 - 1 : H2^' = (0,40 x 1t/m² x 1,70m) x 1m = 0,68 t ; x1 = = 0,85 m

2 - 2 : H2» = (0,40 x 1t/m² x 3,3m) x 1m = 1,32 t ; x2 = = 1,65 m

3 - 3 : H2^''' = (0,40 x 1t/m² x 5,0m) x 1m = 2,0 t ; x3 = = 2,5 m

[101]

? Poussée des terres :

H3 = k x ySol ^x (H3-3)2 , nous évaluons la poussée par zone en tenant compte du sol le plus dominant ;
1 - 1	: H3^' =	0,33 x 1,8 x (1,70m)^2 x 1m = 0,858 t ; x = (1,70m) =						1,13m
2 - 2	: H3^» =	0,33 x 1,8 t/m^3 x (3,3m)^2 x 1m = 3,234 t ; x = (3,3m)						= 2,2m
3 - 3	: H3^''' =	0,40 x 2,6 t/m^3 x (5,0m)^2 x 1m = 13 t ; x = (5,0m) =						3,33m
					^TABLEAU ZONE 1 - ^1
^Zone 1 - ^1				^CHARGE	^Excentricité
^H1				^4	^0,89
^H2 ^0,68 ^0,85
^H3			^0,858		^1,13
^Somme			^5,538		^TABLEAU ZONE 2 - ^2
^Zone 2 - ^2			^CHARGE		^Excentricité		^MOMENT
^H1			^4		^2,49		^9,96
^H2			^1,32		^1,65

[102]

^{TABLEAU ZONE 3} - ³

^{Zone 3} - ³

^CHARGE

^{Excentricité}

7.3.3.2. Calcul de la semelle

^MOMENT

^H1

⁴

^4,19

^16,76

^H2

²

^2,5

⁵

^H3

¹³

^3,33

^43,29

^Somme

¹⁹

^65,05

La semelle est sollicitée par toutes les charges situées au-dessus c'est-à-dire : la réaction

verticale due à l'action des charges provenant de la superstructure, le poids du corps de la

culée, le poids du mur garde grève, le poids du remblai, la surcharge sur remblais et son poids

propre ; en dessous par la réaction du sol. On sait que l'action est égale à la réaction. Nous

considérons l'effet de la réaction du sol sous semelle puisqu'il tend à soulever la semelle.

Nous calculons la semelle comme un élément encastré avec une charge correspondant à la

réaction du sol.

Calcul des moments

Tronçons A - B :

^{18,168 t/m2}

^{0,018 t/m}

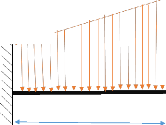
^15,644

^{17,122 t/m2}

^{2,5 m}

FAB1 = x 1m = x 1m = 3,155 t ; x= (2,5) = 1,6m

^2,

FAB2 = 15,644 t/m² x 2,50m x 1m = 39,11 t ; x = (2,50) = 1,25m FAB = 3,155 t + 39,11 t = 42,265 t

[103]

Excentricité : X = = 1,27 m

MAB = - FAB x X = - 42,265 t x 1,27 m = 53,676 tm

Tronçons B - C :

^{12,112 t/m2}

^{3,5 m}

^{15,644 t/m2}

FBC1 = x 1m = x 1m = 6,181 t ; x= (3,5) = 1,16m

FB = 12,112 t/m² x 3,50m x 1m = 42,392 t ; x = (3,50) = 1,75m FBC = 6,181 t + 42,392 t = 48,573 t

Excentricité : X = = 1,67 m

MBC = - _FBC x X = - 48,573 t x 1,67 m = - 81,11691 tm

7.3.3.3. Corbeau

Le corbeau se calcul comme une poutre encastrée d'un seul côté (mur garde grève) par bande d'un mètre.

? Evaluation des charges

Le corbeau sert d'appuis pour la dalle de transition. Nous allons considérer la charge de la dalle de transition par bande d'un mètre et le poids propre du corbeau soit :

[104]

PS = (7,268 t/m² x 1 m) +(0,25m x 1m x 2,5 t/m³) = 7,893 t/m

? Calcul de moment

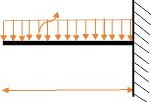
^7,893t/m

^1,0m

M = - = - = - 3,9465 tm

? Calcul de l'effort tranchant

T = PL = 7,893 t/m x 1,0m = 7,893 t