Conception et dimensionnement d'un pont en béton armé de 17,00m de portée à ériger sur la rivière Tshuenge dans la ville province de Kinshasa.

6.4.1.1. Calcul de moment

^0,436875t

^1,50m

^1,6152t/m

^1,50m

M1 = - PL + M2 = -

M1 = 0,436875t x 1,50m = - 0,6553 tm

²

M2 = - 1 , 6 1 52 ( 1 , 5 0 )= - 1,8171 tm

2

Mtotale = - 0,6553 tm - 1,8171 tm = - 2,4724 tm

[73]

6.4.1.1. Calcul de l'effort tranchant

^0,436875t

	^1,50m

T1 = P + T2 = PL

T1 = 0,436875 t

T2 = 1,6152t/m x 1,50m = 2,4228 t

Ttotale = 0,436875t + 2,4228 t = 2,859675 t

[74]

6.5. Calculs d'armatures des éléments de la superstructure

Nous calculons les armatures des éléments de la superstructure aux états limites ultime et nous vérifions les contraintes aux états limites de services cas de la fissuration préjudiciable.

? Poutres principales :

MU = 506,7696848 tm et TU = 116,3882494 t ; M_s = 356,7453406 tm et Ts = 82,0389625 t

· Largeur de la table de compression :

Nous utilisons la formule suivante : B = 12hd + bO = 12(0,18) + 0,50 = 2,66 m

Nous avons : B = 2,66 m ; d = h_p - e = 1,50 - 0,05 = 1,45 m ; f8 = 30 MPa alors

fbu = _ = 17 MPa or 1 MPa = 100 t/m2 -- fbu = 1700 t/m2 ; f_e = 500 MPa alors

f_s = = 434,78 MPa 435 MPa = 43500 t/m2

· Moment résistant de la table de compression :

Mt = B x hO x _fbu (d - ² ) = 2,66m x 0,18m x 1700 t/m2 x (1,45m - ² ) = 1106,9856 tm

M_u < Mt ; d'où la poutre est simplement armée.

· Moment réduit ultime :

ìbu = ~~v = 0,053 < 0,186 (pivot A)

=

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,068

· Position de l'axe neutre :

y = á x d = 0,068 x 1,45 = 0,0986 m -- la position est donnée tel que : 0,8.y < hd ; nous aurons : 0,8 x 0,0986m < 0,18 -- 0,0788 < 0,18 (Poutre rectangulaire)

St < 22,0 cm ? St = 20 cm

[75]

· Bras de levier :

Z = d (1 - 0,4 á) = 1,45 (1 - 0,4(0,068)) = 1,41 m

· Armatures principales :

AS = = 0,008262 m2 = 82,62 cm² soit 12HA30 ? 84,78 cm²

· Armatures transversales : T_u = 116,3882494 t

La contrainte tangentielle ultime moyenne : ôuo = = = 160,5355 t/m²

Etant donné qu'on est en fissuration peu préjudiciable

ôlim < min (

; 5 MPa)

ôlim < min ( ; 5 MPa)

ôlim < min (4MPa ; 5 MPa) ôlim = 4 MPa = 400 t/m²

ôuo ? ôlim ; d'où l'utilisation des armature transversale droite.

Section d'armature doit être tel que: dit < min ( ; ; )

dit < min ( ; ; 30mm )

dit < 30mm ; nous adoptons : dit = 12 mm

= =

At = 113,04 mm² = 1,1304 cm²
At = 1,1304 cm2 x 4 brins = 4,5216 cm2

· Ecartement d'armatures :

S < t-= -

= 0,220 m = 22,0 cm

verifié.

[76]

· Armatures de peau :

A_p ? x parement( 2R+bo) ? A_p ? x ( 2(1,32)+0,50)

A_p ? 9,42 cm² soit 4HA18 ? 10,18 cm²

Vérification des contraintes

MS = 356,7453406 tm ; d = 1,45m ; b = 2,66m ; AS = 84,78 cm² ; f8 = 30 MPa ; f_e = 500MPa

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

	- 0,1407348(1,45 - y) = 0				(2,66) - 16,6 (0,008478)(1,45 - y) = 0 ? 2,66
	+ 0,1407348 y - 0,20406546		= 0	? 2,66 y^2 + 0,2814696 y - 0,40813092 = 0
				? = b^2 - 4ac = (0,2814696) ^2 - 4(2,66) (-0,40813092)
=	4,349

v = #177;2,085

= 0,339 m

y =

· Moment d'inertie : I = Ib + nISt

avec Ib = y³ = (0,339)³ = 0,0345 m⁴ et ISt = AS (d - y)² = 0,008478(1,45 - 0,339)² =

0,01046 m4

I = Ib + nISt = 0,0345m⁴ + 16,6(0,01046 m⁴⁾ = 0,208136 m4

Les contraintes sont : c = Ms

xy = 581,046 t/m² et fst= n.Ms(d--y)

f = 31610,637 t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

[77]

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : f _st = min{ ³ f e ; max (0,5 f e ;110.nf t28}
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m² f = min{ (50000) ;m (0,5 50

st 000 ;110.1,6(240)}
f = min{ 33333,3 ;m (25000 ;2

st 155,55)} ; nous adoptons f st = 25000 t/m² ; nous
savons que : fSt ? f ^st la condition n'est pas vérifiée dans ce cas nous recalculons la section d'aciers tendus aux états limites de service.

Calcul d'armature :

·		, =
	0,544
Axe neutre : y = á x d = 0,544 x 1,45m = 0,79m				·
, levier	1,187m
Moment résistant de la table : MRS = (b x y)	x Z = (2,66 x 0,79 )	1800 x 1,187

MRS = 2244,925 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = 0,012021 m² = 120,21 cm² soit 16HA32 ? 128,61 cm²

= ,

? Entretoises :

· En travée :

Mû = 71,2557 tm et Mu- = 4,347675 tm

· Largeur de la table de compression : B = 12ho + bo = 12(0,18) + 0,40 = 2,56m

MS = 47,5038 tm ; d = 1,27m ; b = 2,56m ; AS = 14,73 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

[78]

Donnés : B = 2,56 m ; d = hP - e = 1,32 - 0,05 = 1,27m ; fbu = 1700 t/m² ; fsu = 43500 t/m²

· Moment de la table :

Mt = b x ho x _fbu x (d - ) = 2,56m x 0,18m x 1700 x (1,27 - ) = 924,3648 tm

· Pour le moment positif : Mû = 71,2557 tm M_u < Mt : section rectangulaire (B x h)

= 0,010151 < 0,186 (pivot A)

ìbu = =

á = 1,25 (1 - v ) = 0,01275

Z = d (1 - 0,4 á) = 1,27 (1 - 0,4(0,01275)) = 1,2635

_ _

AS 1 - 0,00129644 m2 = 12,9644 cm² soit 3HA25 ? 14,73 cm²

· Pour le moment négatif : Mu- = 4,347675 tm

= .( = 0,00061938 < 0,186 (pivot A)

ìbu = (1

b 1700.,27)x.2

á = 1,25 (1 - v ) = 0,00077446

Z = d (1 - 0,4 á) = 1,27 (1 - 0,4(0,00077446)) = 1,2696m

AS = _ = 0,00007872 m2 = 0,7872 cm² soit 4HA8 ? 2,01 cm²

· Armatures de peau :

A_p > x parement( 2R+bo) ? A_p > x ( 2(1,14)+0,40)

A_p > 8,04 cm² soit 4HA16 ? 8,04 cm²

Vérification des contraintes

Pour le moment positif :

[79]

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

(2,56) - 16,6 (0,001473)(1,45 - y) = 0 ? (2,56) - 0,02445(1,45 - y) = 0

? (2,56) - 0,03545 + 0,02445 y = 0 ? 2,56 + 0,02445 y - 0,03545 = 0

? 2,56 y² + 0,0489 y - 0,0709 = 0

? = b² - 4ac = (0,0489) ² - 4(2,56) (-0,0709) = 0,7284 v = 0,85

y = = 0,156 m

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,156)³ = 0,003239 m⁴ et ISt = AS (d - y)² = 0,001473(1,27 - 0,156)² =

0,00183 m4

I = Ib + nISt = 0,03239m⁴ + 16,6(0,00183 m⁴⁾ = 0,033617 m4

Les contraintes sont : fbc = = 220,44 t/m² et fSt = = 26131,39t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }

Avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{

v }

[80]

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

d'aciers tendus aux états limites de service. Calcul d'armature : · Paramètre de déformation : á =		=		= 0,544

· Axe neutre : y = á x d = 0,544 x 1,27m = 0,69 m

· Bras de levier : Z = d (1 - ) = 1,27(1 - ) = 1,039m

· Moment résistant de la table : MRS = (b x y) x Z = (2,56 x 0,69 ) 1800 x 1,039

MRS = 1651,760 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = = 0,001829 m² = 18,29 cm² soit 6HA20 ? 18,84 cm²

· Aux appuis :

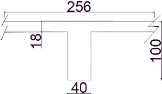
B = 2,56 m ; d = h_p - e = 1 - 0,05 = 0,95 m ; fbu = 1700 t/m² ; fsu = 43500 t/m²

· Moment de la table de compression :

Mt = 2,56 x 0,18 x 1700 x ( 0,95 - ) = 673,6896 tm

M_u ? Mt : section rectangulaire (B x h)

· Moment réduit ultime :

ìbu == 0,018141 ? 0,186 (pivot A)

=

· Paramètre de déformation :

[81]

á = 1,25 (1 - v ) = 0,02288

· Bras de levier :

Z = d (1 - 0,4 á) = 0,95 (1 - 0,4(0,02288)) = 0,939m

· Section d'armature :

AS = = 0,0017444 m2 = 17,444 cm² soit 6HA20 ? 18,84 cm²

· Pour le moment négatif : Mu^- = 4,347675 tm

ìb

=
· = 0 001106 < 0 186(pivot
u = , ₇ A)

á = 1,25 (1 - v ) = 0,001383

Z = d (1 - 0,4 á) = 0,95 (1 - 0,4(0,001383)) = 0,949m

AS = = 0,0001053 m² = 1,053 cm² soit 4HA8 ? 2,01 cm²

Pour les armatures transversales, nous adoptons les même que celles des poutres.

· Armatures de peau :

A_p ? x parement( 2R+bo) ? A_p ? x ( 2(0,82)+0,40)

A_p ? 6,12 cm2 soit 4HA14 ? 6,16 cm²

Vérification des contraintes

Pour le moment positif :

MS = 47,5038 tm ; d = 0,95m ; b = 2,56m ; AS = 18,84 cm² ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre :

b - nAS (d - y) = 0 ; avec n = = = 16,6

(2,56) - 16,6 (0,001884)(0,95 - y) = 0 ? (2,56) - 0,03127(0,95 - y) = 0

? (2,56) - 0,0297 + 0,03127 y = 0 ? 2,56 + 0,03127 y - 0,0297= 0

? 2,56 y² + 0,06254 y - 0,0594 = 0

[82]

? = b² - 4ac = (0,06254) ² - 4(2,56) (-0,0594) = 0,61217 v = 0,78

y = = 0,14 m

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,14)³ = 0,0023 m⁴ et ISt = AS (d - y)² = 0,001884(0,95 - 0,14)² =

0,001236 m4

I = Ib + nISt = 0,0023 m⁴ + 16,6(0,001236 m⁴⁾ = 0,0228 m4

Les contraintes sont : fbc = = 291,68 t/m² et fSt = = 28014,74t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m² ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

=

d'aciers tendus aux états limites de service.

· Calcul d'armature :

·

= 0,544

Paramètre de déformation : á =

· Axe neutre : y = á x d = 0,544 x 0,95m = 0,5168 m

· Bras de levier : Z = d (1 - ) = 0,95(1 - ) = 0,778m

verifié.

[83]

· Moment résistant de la table : MRS = (b x y) x Z = (2,56 x 0,5168 ) 1800 x 0,778

MRS = 926,37 tm ? MS (poutre simplement armée)

· Sections d'armature :

AS = = 0,002442 m² = 24,42 cm² soit 8HA20 ? 25,14 cm²

Pour le moment négatif :

MS = 2,89845 tm ; d = 0,95m ; b = 2,56m ; AS = 2,01 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre :
b - nAS (d - y) = 0 ; avec n =	=		=	16,6
(2,56) - 16,6 (0,000201)(0,95	- y) =	0	?	(2,56)	- 0,0033366(0,95 - y) = 0

? (2,56) - 0,003169 + 0,0033366 y = 0 ? 2,56 + 0,0033366 y - 0,003169 = 0

? 2,56 y² + 0,0066732 y - 0,006338 = 0

? = b² - 4ac = (0,0066732) ² - 4(2,56) (-0,006338) = 0,06494 v = 0,2548

y

= = 0,048 m

· Moment d'inertie : I = Ib + nISt

avec Ib = y³ = (0,048)³ = 0,000094 m⁴ et ISt = AS (d - y)² = 0,000201(0,95 - 0,048)² =

0,00016 m4

I = Ib + nISt = 0,000094 m⁴ + 16,6(0,00016 m⁴⁾ = 0,00275 m4

Les contraintes sont : fbc = = 50,59 t/m² et fSt = = 15781,48 t/m²

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m2 ; nous savons que : fbc ? la condition est

[84]

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? ? Dalle : · En travée :

la condition est vérifiée

Suivant le sens transversale(x) :

Mû = 12,3188698 tm ; d = 0,18m - 0,05m = 0,13m ; b =1m

· Moment réduit ultime :

' = 0,4287 0,430 ? 0,186 (doublement armé)

ìbu = =

· Sections d'armatures :

As = fl_u x b x d x et As^' = fl_u^' x b x d x avec : fl_u = 0,5591 et fl_u^' = 0,0656

· Armatures inférieures :

As = 0,5591 x 1,00 x 0,13 x = 0,00284 mm² = 28,4 cm² soit 12HA18/m ?30,52 cm²

· Armatures supérieures :

As^' = 0,0656 x 1,00 x 0,13 x = 0,00033327 = 3,3327 cm² soit 3HA14/m ? 4,62 cm²

Suivant le sens de la circulation(y) :

Mû = 3,07971745 tm ; d = 0,18m - 0,05m = 0,13m ; b =1m

· Moment réduit ultime :

--

M

=

= 0107 < O 186

ìbu-- , 7

[85]

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,141

· Bras de levier :

Z = d (1 - 0,4 á) = 0,13 (1 - 0,4(0,141)) = 0,122m

· Section d'armature :

AS = = 0,0005803 m² = 5,803 cm² soit 8HA10/m ? 6,28 cm²

· Aux appuis : M_u^- = 7,246394 tm

· Moment réduit ultime :

ìbu = =

= 0,252 ? 0,186

0,186 ? 0,2522 ? 0,371 (dalle simplement armée)

As = â_u x b x d x avec : â_u = 0,2957

· Section d'armatures :

As = 0,2957 x 1,00 x 0,13 x = 0,0015022 m² = 15,022 cm² soit 10HA14/m ? As =

15,39 cm²

· Espacement :

Stx = min { = min { ? Stx = 33cm l'espacement entre les barres principales d'une

dalle ne dépasse pas 30 cm.

Sty = min { = min { ? Sty = 44cm.

? Encorbellement : Mu^- = 2,4724 tm

· Moment réduit ultime :

[86]

= 0,086 ? 0,186 (pivot A)

ìbu = =

· Paramètre de déformation :

á = 1,25 (1 - v ) = 0,112

· Bras de levier :

Z = d (1 - 0,4 á) = 0,13 (1 - 0,4(0,112)) = 0,124 m

· Section d'armatures :

AS =

_ = 0,0004583 m2 = 4,583 cm² soit 3HA14 /m? 4,62 cm² Armatures de répartition : Ar = ; ( 4,62) = 1,155 cm² soit 2HA10 ? 1,57 cm² ? Vérification de l'effort tranchant :

? 21,9975 < 182,60869 : condition vérifiée

< <

?

· Espacements :

Stx < min { < min { ? Stx < 33cm l'espacement entre les barres principales d'une

dalle ne dépasse pas 30 cm. D'où nous adoptons Stx = 20 cm

Sty < min { < min { ? Sty < 44cm. D'où nous adoptons Sty = 30 cm

Vérification des contraintes

MS = 1,76475 tm ; d = 0,13m ; b = 1,0 m ; AS = 4,62 cm2 ; f8 = 30 MPa ; f_e = 500 MPa

· Position de l'axe neutre : b - nAS (d - y) = 0 ; avec n = = = 16,6

(1) - 16,6 (0,000462)(0,13 - y) = 0 ? - 0,00767(0,13 - y) = 0

? - 0,00099 + 0,00767 y = 0 ? + 0,00767 y - 0,00099 = 0

? y² + 0,01534 y - 0,00198 = 0

[87]

? = b² - 4ac = (0,01534) ² - 4(1) (-0,00198) = 0,0081 v = 0,09

= 0,037 m

y =

· Moment d'inertie :

I = Ib + nISt

avec Ib = y³ = (0,037)³ = 0,0000168 m⁴ et ISt = AS (d - y)² = 0,000462(0,13 - 0,037)² =

0,00000399 m4

I = Ib + nISt = 0,0000168 m⁴ + 16,6(0,00000399 m⁴⁾ = 0,0000830 m4

fb_c = M =fst= n. = 32824,35 t/m²

Les contraintes sont : 786 69 t/m² et

· Contrainte limite de compression du béton :

= 0,6 f8 = 0,6(30) = 18 MPa = 1800 t/m2 ; nous savons que : fbc ? la condition est

verifié.

· Contrainte limite de traction de l'acier :

Fissuration préjudiciable : = min{ v }
avec : ç = 1,6 (haute adhérence) ; ft28 = 0,6 + 0,06 f8 = 0,6 + 0,06(30) = 2,4 MPa = 240 t/m²

= min{ v }

= min{ } ; nous adoptons = 25000 t/m² ; nous

savons que : fSt ? la condition n'est pas vérifiée dans ce cas nous recalculons la section

d'aciers tendus aux états limites de service. Calcul d'armature : · Paramètre de déformation : á =		=		= 0,544

· Bras de levier : Z = d (1 - ) = 0,13(1 - ) = 0,106 m

· Moment résistant de la table : MRS = (b x y) x Z = (1 x 0,07 ) 1800 x 0,106

[88]

MRS = 6,678 tm ? MS (poutre simplement armée) ? Sections d'armature :

AS = = = 0,000665 m² = 6,65 cm² soit 5HA14 ? 7,70 cm²

Armatures de répartition : Ar = ( 7,70) = 1,92 cm² soit 3HA10 ? 2,36 cm2

[89]

CHAPITRE.7. Calcul des éléments de l'infrastructure

Dans ce chapitre, nous allons évaluer les charges, étudier la stabilité des éléments de l'infrastructure (en considérant les charges en ELU pour l'appareil d'appuis). Enfin, nous allons faire le calcul du béton armé aux états limite de services.