B. L'analyse de la régression multiple
La régression linéaire est une technique
statistique permettant de construire un lien entre une variable explicative
(indépendante) et une variable expliquée (dépendante). Le
but est soit de prédire la variable expliquée lorsqu'on connait
la variable explicative ou d'établir une relation s'il y a un effet
d'une des variables sur l'autre. A cet effet, dans le cadre de notre
recherche, pour tester nos hypothèses, c'est le modèle
linéaire multiple que nous avons utilisé.
1. Définition de la méthode de
régression multiple
En général, les modèles de
régression sont construits dans le but d'expliquer (ou prédire,
selon la perspective de l'analyse) la variance d'un phénomène
(variable dépendante) à l'aide d'une combinaison de facteurs
explicatifs (variables indépendantes). Dans le cas de la
régression linéaire multiple, la variable dépendante est
toujours une variable continue tandis que les variables indépendantes
peuvent être continues ou catégorielles. La régression
linéaire est appelée multiple lorsque le modèle est
composé d'au moins deux variables indépendantes.
Ainsi pour   variables indépendantes, le modèle s'écrit : variables indépendantes, le modèle s'écrit :
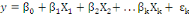
Où 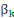 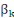 représentent les coefficients de régression partielle, représentent les coefficients de régression partielle,
 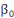 la valeur prise par la variable dépendante la valeur prise par la variable dépendante   lorsque les coefficients des variables indépendantes sont nuls, lorsque les coefficients des variables indépendantes sont nuls,
  les variables indépendantes et les variables indépendantes et 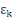 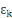 le terme d'erreur. Nous notons déjà que tous les calculs
seront faits à l'aide du logiciel SPSS. le terme d'erreur. Nous notons déjà que tous les calculs
seront faits à l'aide du logiciel SPSS.
2. Interprétation des indicateurs de l'analyse
de régression multiple
Quel que soit la méthode utilisée pour une
analyse statistique, c'est de la pertinence de l'interprétation des
résultats que découle la pertinence de la méthode choisie.
Dans le cadre de l'analyse de régression, l'interprétation des
résultats se fait à trois niveaux :
Le coefficient de
détermination : Ce coefficient sert à mesurer
la qualité de l'ajustement entre les variables de l'analyse. En effet,
plus les variables expliquées sont « proches » de la
variabilité totale, meilleure est l'ajustement global du modèle.
La définition de ce coefficient se fonde sur la forme de
décomposition de variabilité. Elle s'exprime par le rapport
variabilité expliquée/variabilité totale. R2
mesure la proportion de la variance de Y expliquée par la
régression de Y sur X et est donné par la relation
suivante :

Interprétation du F de Fisher :
le test F de Fisher permet de tester si le modèle
linéaire rend compte de manière significative le comportement de
la variable dépendante. Plus la probabilité de dépassement
de la valeur est faible, plus la signification est grande. Dans ce test, les
degrés de liberté correspondent au nombre de valeurs que nous
pouvons choisir arbitrairement. La statistique de F est le rapport de la somme
des carrés expliqués par 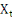 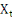 sur la somme des carrés des résidus, chacune de ces
sommes étant divisée par son degré de liberté
respectif. Ainsi, si la variance expliquée est significativement
supérieure à la variance résiduelle, la variable sur la somme des carrés des résidus, chacune de ces
sommes étant divisée par son degré de liberté
respectif. Ainsi, si la variance expliquée est significativement
supérieure à la variance résiduelle, la variable 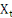 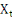 est considérée comme étant une variable
réellement explicative. Dans la plupart des cas, on accepte
l'hypothèse de la significativité du modèle si la
probabilité de F est inférieure ou égale à 0,05. est considérée comme étant une variable
réellement explicative. Dans la plupart des cas, on accepte
l'hypothèse de la significativité du modèle si la
probabilité de F est inférieure ou égale à 0,05.
Interprétation du t de Student :
la statistique t de Student est utilisée pour tester les
coefficients   des variables explicatives du modèle de régression. On
dira que ces variables sont significatives si et seulement si les t de Student
calculés par le modèle sont significatifs, c'est-à-dire
que les coefficients des variables explicatives du modèle de régression. On
dira que ces variables sont significatives si et seulement si les t de Student
calculés par le modèle sont significatifs, c'est-à-dire
que les coefficients   ont des t Student supérieur ou égale 2 avec des
probabilités inférieures à 0,05. ont des t Student supérieur ou égale 2 avec des
probabilités inférieures à 0,05.
| 


