Chapitre II : Gisement solaire et le
générateur photovoltaïque

Fig. IV. 20 Les Résultats de la simulation du
démarrage à vide du moteur asynchrone.
L'oscillogramme de la figure IV. 20 représente
l'évolution du courant, de la vitesse et du couple au démarrage
d'un moteur asynchrone à vide. On note un appel d'un fort courant
à la mise sous tension ; la valeur instantanée de ce courant peut
atteindre trois fois le courant nominal pour le cas étudié. Des
oscillations de couple apparaissent et peuvent atteindre trois fois le couple
nominal, après disparition du régime transitoire, le couple tend
vers zéro puisque le couple résistant et nul.
? Remarque : Le démarrage à vide et sous tension
nominale permet un
établissement rapide de la vitesse et un couple
électromagnétique instantané. L'application d'une charge
introduit une chute de vitesse.
Lorsque la charge est appliquée, le couple
électromagnétique répond instantanément et la
vitesse est légèrement perturbée. La commande en courant
donne une réponse à fort dépassement pour le couple
électromagnétique par conséquent il est
déconseillé de l'utiliser dans un système à boucle
ouverte pour des raisons de stabilité.
3.4. Commande scalaire
Cette technique est facile d'implantation, moins
coûteuse donnant aussi des performances statiques acceptables plusieurs
commandes scalaires existent selon que l'on agit sur le courant ou sur la
tension. Elles dépendent surtout de la topologie de l'actionneur
utilisé (onduleur de tension ou de courant) et pour notre cas on a
utilisé l'onduleur de tension alimentant la machine asynchrone
commandée par une commande scalaire
(V/f)=cst (Figure IV. 21).
Chapitre II : Gisement solaire et le générateur
photovoltaïque
Tracker Solaire Page 54
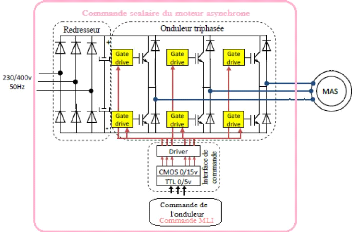
Fig. IV. 21 Commande scalaire du moteur asynchrone [22].
3.4.1. Contrôle en V/f de la machine
asynchrone
Son principe est de maintenir V/f = Constant
ce qui signifie garder le flux constant. Le contrôle du couple se fait
par l'action sur le glissement. En effet, d'après le modèle
établi en régime permanent, le couple maximum s'écrit :
( ) E. 51
On voit bien que le couple est directement proportionnel au
carré du rapport de la tension sur la fréquence statorique
[23].
3.4.2. Modélisation de l'onduleur triphasé
La figure IV. 22 présente le schéma d'un onduleur
triphasé alimentant le MAS [24].
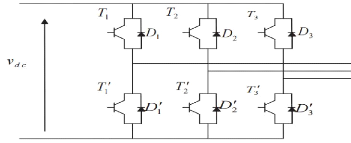
Fig. IV. 22 Le schéma d'un onduleur triphasé
alimentant le MAS.
L'onduleur de tension triphasé se compose de trois bras
identiques. Chaque bras composé de deux cellules comportant chacune une
diode et un transistor. Tous ces éléments sont
considérés comme des interrupteurs parfaits
[24]. Alors l'onduleur de tension peut être
représenté dans le cas idéal sous la forme suivante dans
la figure IV.24.
Chapitre II : Gisement solaire et le générateur
photovoltaïque

Tracker Solaire Page 55
Fig. IV. 23 Schéma équivalent de
l'onduleur.
L'onduleur est modélisé en associant à
chaque bras une fonction logique F qui détermine son état de
conduction [24] :
{
1 si Icifermé et Ici' ouvert Avec i=1,
2, 3.
0 si Ici'fermé et Ici ouvert L'expression
sous forme matricielle des tensions simples de l'onduleur au
moyen des fonctions logiques de connexions est obtenue à
partir des équations :
(Vas(2 --1 --1 F1
Vbs = v3c--1 2 --1 F2 E. 52
Vcs --1 --1 2 F3
Vdc: C'est la tension d'alimentation continue de
l'onduleur.
Le modèle (E.52) peut être représenté
sous Simulink par le schéma suivant figure IV. 24 :

Fig. IV. 24 Modèle de l'onduleur
triphasé.
La figure VI. 25 suivante illustre la forme des tensions obtenus
à la sortie de l'onduleur.
Chapitre II : Gisement solaire et le générateur
photovoltaïque

Fig. IV. 25 La sortie d'onduleur triphasé.
| 


