Chapitre II : Gisement solaire et le
générateur photovoltaïque
Calcul de la course du vérin [19] :
X = XO -- ( h * cos (elévation) + C2 -- ( e
+ h * sin(elévation)2)) E. 49
X0 : Position du vérin par rapport à l'état
initial.
X = + 2+e2
0
X : sortie du vérin par rapport à sa position
initiale.
3.3.5. Estimation du couple résistant
Le couple résistant est supposé nul pour le
mouvement en azimut (Cr Azimut =0), car ce mouvement n'est pas
influencé par la gravité et en adoptant l'hypothèse qu'il
n'y a pas d'efforts externes (perturbation). Pour le mouvement en
élévation, le couple résistant évolue avec l'angle
d'élévation du tracker. L'expression du couple résistant
est donc écrite sous la forme suivante [13]:
(elévation) * d E. 50
Avec mplateau+modules, g et d sont
respectivement la masse du plateau et des modules, l'intensité de la
pesanteur (9,81 m/s2) et la distance entre le centre de
gravité et le centre de la rotation.
3.3.6. Modélisation et simulation du modèle
dynamique
Il s'agit dans ce volet de faire la simulation du
modèle dynamique d'un moteur asynchrone, ainsi on est amené
à élaborer l'ensemble des équations qui
caractérisent ce modèle et l'implanter sur MATLAB et plus
précisément sous son module de simulation SIMULINK (Figure. IV.
17).
L'interface principale du simulateur ainsi que les
différents blocs principaux développés sont
présentés ci-après.
a) Diagramme fonctionnel du MAS
Tracker Solaire Page 50
Tracker Solaire Page 51
Chapitre II : Gisement solaire et le générateur
photovoltaïque

Fig. IV.17 Modéle Interne du MAS.
La machine asynchrone présente des entrées :
? ws (1), Vds (2), Vqs
(3) : composantes de PARK et pulsation de la tension d'alimentation.
? Le couple résistant Cr (4), caractéristique de la
charge.
Les sorties suivantes sont accessibles : Ids (3),
Iqs (4) composantes de PARK du courant moteur, Ce
(6) : couple moteur (Ce) et w (7) vitesse de rotation.
b) Démarrage direct du moteur
Il faut encore réaliser la transformée
de PARK du réseau d'alimentation pour l'appliquer au
schéma fonctionnel du moteur et calculer l'angle 8ypar
intégration decoy.
La transformation de PARK inverse permet de revenir aux
grandeurs réelles de la machine (courant I dans notre cas). C'est ce qui
est présenté dans le schéma suivant (figure IV. 18) :

Fig. IV. 18 Modèle en bloc Simulink de la MAS
alimentée en tension.
Chapitre II : Gisement solaire et le générateur
photovoltaïque
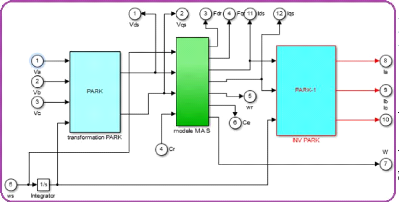
Fig. IV. 19 Le schéma interne de MAS modèle
dq.
Le bloc MAS correspond à la
modélisation faite plus haut. Sources sinusoïdales
triphasées est une source triphasée
équilibrée de tension de valeur efficace 230 V et de
fréquence 50 Hz. PARK permet de calculer les
composantes de PARK du réseau de tension et PARK-1
permet de reconstituer les courants absorbés par le moteur
à partir de ses composantes de PARK. L'intégrateur
permet d'obtenir sà partir de l'intégration de
wS.
c) Résultats de la modélisation
La simulation du modèle présenté dans la
figure IV. 18 donne des réponses en boucle ouverte de la machine
asynchrone à vide comme la figure IV. 20 suivante:
Tracker Solaire Page 52
Tracker Solaire Page 53
| 


