3.10. Estimation des taux de
transition
3.10.1. Exposition au risque
L'exposition au risque est le temps vécu par un
individu entre l'âge x et l'âge x+1
L'exposition au risque dans l'état actif à
l'âge x (ou années révolues) vaut :
ERa(x)=temps total passé en activité
par les femmes d'âge x au cours d'une période
ERa(x)=  , ou , ou 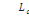  désigne le nombre des femmes ayant occupé l'état
« actif » à l'âge x, et désigne le nombre des femmes ayant occupé l'état
« actif » à l'âge x, et   la durée d'activité de la ième
femme. la durée d'activité de la ième
femme.
L'exposition du risque dans l'état
hospitalisé
Elle vaut ERh(x)=temps total passé à
l'hôpital par les femmes d'âge x au cours d'une période
ERh(x)=  , ou , ou   désigne le nombre des femmes ayant effectué un
séjour à l'hopital à l'âge x, et désigne le nombre des femmes ayant effectué un
séjour à l'hopital à l'âge x, et   la durée d'hospitalisation de la IVème
femme. la durée d'hospitalisation de la IVème
femme.
L'exposition du risque dans l'état hospitalisé
pour un accouchement
Cette exposition vaut
ERg(x)=temps total passé à
l'hôpital pour un accouchement par les femmes d'âge x au cours
d'une période
ERg(x)=  , ou , ou   désigne le nombre des femmes ayant effectué un
séjour à l'hopital suite à une grossesse à
l'âge x, et désigne le nombre des femmes ayant effectué un
séjour à l'hopital suite à une grossesse à
l'âge x, et   la durée d'hospitalisation de la ième
femme. la durée d'hospitalisation de la ième
femme.
3.10.2. Estimation brut des taux de transition
On dispose pour un grand nombre de femmes leurs observations
sur une ou plusieurs années, les temps de séjour dans les
différents états (temps écoulé entre transition
successives et nombre de transitions de chaque type)
Soit   , ,  , ,  , ,  le risque relatifs pour un assuré d'âge x d'être
dans un état d'hospitalisation, d'activité ou d'accouchement. La
fonction de vraisemblance relatif à cet observation est L( le risque relatifs pour un assuré d'âge x d'être
dans un état d'hospitalisation, d'activité ou d'accouchement. La
fonction de vraisemblance relatif à cet observation est L(  , ,  , ,  , ,  (x)). (x)).
Chaque période de durée Ät passé par
un assuré d'âge x dans l'état « actif »
contribue à hauteur d'un facteur exp(-(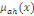  + +  ), la même période passé à l'état
hospitalisé à hauteur de exp(- ), la même période passé à l'état
hospitalisé à hauteur de exp(-  Ät ) et enfin dans l'état accouchement à hauteur de
exp(- Ät ) et enfin dans l'état accouchement à hauteur de
exp(-  Ät). Ät).
Chaque passage de e0 à e1, de e1 à e2, de e1
à e0 et de e2 à e0 contribue respectivement à la
vraisemblance à hauteur d'un facteur  , d'un facteur , d'un facteur  , d'un facteur , d'un facteur   et enfin d'un facteur et enfin d'un facteur  . .
Il faut mémoriser la durée totale passée
par les assurées dans les différents états en
répertoriant les expositions et le nombre de transition
effectuées par ces assurées.
Notons alors,
  : le nombre de transition de l'état actif à celui
d'hospitalisé effectué par l'assuré j d'âge x. : le nombre de transition de l'état actif à celui
d'hospitalisé effectué par l'assuré j d'âge x.
  : le nombre de transition de l'état hospitalisé à
celui d'actif effectué par l'assuré j d'âge x. : le nombre de transition de l'état hospitalisé à
celui d'actif effectué par l'assuré j d'âge x.
  : le nombre de transition de l'état actif à celui
d'hospitalisé pour une grossesse effectué par l'assuré j
d'âge x. : le nombre de transition de l'état actif à celui
d'hospitalisé pour une grossesse effectué par l'assuré j
d'âge x.
  : le nombre de transition de l'état hospitalisé pour une
grossesse à l'état actif effectué par l'assuré j
d'âge x. : le nombre de transition de l'état hospitalisé pour une
grossesse à l'état actif effectué par l'assuré j
d'âge x.
Posons   = =  , ,  = =  , ,  = =  , ,  = = 
Les observations relatives à ces variables sont  , ,  , ,  , , 
La fonction de vraisemblance associée à un individu
d'âge fixe peut s'écrire
L(  , ,  , ,  , ,  (x))= exp[-( (x))= exp[-(  + +  ]. exp[-( ]. exp[-(  ]. ].
exp[-(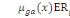  ] ]   (3.9) (3.9)
En passant à la log de vraisemblance, puis en annulant les
dérivées partielles par rapport aux quatre paramètres   , ,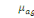  , ,  , ,  (x), il vient (x), il vient
  ; ;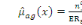  ; ;  ; ;  sont des estimateurs de maximum de vraisemblance non contraints, ou
brut, des taux instantanés de transition entre différents
états de figure Fig3.2. sont des estimateurs de maximum de vraisemblance non contraints, ou
brut, des taux instantanés de transition entre différents
états de figure Fig3.2.
| 


