Estimation non-paramétrique par noyaux associés et données de panel en marketing

Chapitre 3

Noyau associé continu asymétrique

Dans ce chapitre nous commen_çons par donner la définition dun no_yau associé continu. A partir de cette définition, nous présentons lestimateur a no_yau associé continu as_ymétri_que dans le cas univarié puis multivarié. Nous étudions les propriétés élémentairesdecetestimateur.Différentsexemplesseronttraitésen_guisedeconclusion.

3.1 Cas univarié

Danscettepremièrepartie,nousprésentonslestimateurano_yauassociécontinuas_ymétri_que dans le cas univarié. Cet estimateur est approprié pour estimer des densités a support compact ou bornées d'un côté. Nous allons traiter _quatres no_yaux di~érents _gamma, bêta, _gaussien inverse (IG) et _gaussien inverse récipro_que (RIG) Pour de réé centes références nous pouvons consulter Chen (1999 2000) et Scaillet (2004) Nous montrons les propriétés élémentaires telles _que biais, variance et MISE. Ensuite nous déterminons les fenêtres optimales pour cha_que no_yau associé considéré et lerreur en fonction de ces valeurs.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires iid de densité de probabilité continue inconnue f a support = [a,b], avec a E R et b E R ( est par exemple le support [0,1] ou [0, + 8[). De manière _génèrale, l'estimateur a no_yau continu est de la forme suivante:

^bfn(x) = 1 n

Xn i=1

(3.1) Kx,h(Xi)

= ^bfn,h,K(x),

on x est fixé dans , Kx,h est la fonction no_yau associéU et h est un réel strictement positif appelé paramètre de lissa_ge.

Dans le cas on Kx,h est associé a un no_yau continu s_ymétri_que il vérifie

~x - . ~

1

Kx,h(.) = _hK .

h

Dans le cas purement as_ymétri_que, Kx,h est un no_yau variable en fonction de la cible x (point d'estimation). Il chan_ge de forme cha_que fois _que x varie dans .

3.1.1 Definition

Definition 1: Soit x ? ? et h > 0. Nous appelons "no_yau associe continu "" Kx,h toute densit( de probabilit( dune variable aléatoire Kx,h sur le support ?x,h tels _que:

?x,h n ? =6 Ø	(3.2)
?x?x,h ? ?	(3.3)
E(Kx,h) ~ x quand h ? 0	(3.4)
V ar(Kx,h) < co	(3.5)
V ar(Kx,h) ? 0 quand h ? 0.	(3.6)

Commentaires::

a. La relation (3.2) traduit le fait _que l'intersection entre le support des observations et le support du no_yau associé continu as_ymétri_que doit contenir au moins un élement. Pour un h fixé, _quand x parcourt ?, le support ?x,h chan_ge, l'expression (3.3) suppose _que ? doit etre tou_jours contenu dans la réunion des ?x,h. La condition (3.4) permet d'assurer la conver_gence ponctuelle de l'estimateur ; elle met en évidence _que le no_yau K_x,h est un no_yau variable ou adaptif a la cible x. Par analo_gie au cas continu s_ymétri_que, la relation (3.5) n'est _que la formule annoncée dans (25) du chapitre précédent. Enfin, la relation (3.6) assure la conver_gence de la variance de la variable aléatoire du no_yau associé et va nous servir dans les calculs suivants.

b. Avant _que nous passons a l'étude des des no_yaux continus as_ymétri_ques, nous reveFIG. 3.1 - Densit( de loi norinale centrée

Densité de la loi normale

0.0 0.1 0.2 03 0A

th30040)

-6 -4 -2 0 2 4 6

x

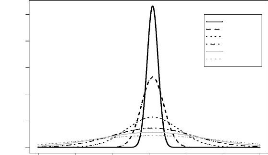
FIG. 3.2 -- Illustration de la densite normale pour h = 1.5 et x = y varie

0.00 0.05 0.10 0.15 0.20 0.25

K(Y)

1	Xn i=1	~ ~ exp -1 (Xi x)2 . 2 h2
nhv2ð

-10 -5 0 5 10

y

male N(u,ó²) est une loi continue définie sur ? = R de densité de probabilité gN(u,ó²) telle _que

~ ~

1 _-1 (x - u)²

gN(u,ó²)(x) = v2ðó2 exp .

2 ó2

Si X est une variable aléatoire _qui suit la loi normale alors lespérance et la variance sont respectivement

E(X) = u et V ar(X) = ó².

La fi_gure 3.1 donne l'allure _génerale d'une densité normale centrée Soit _KN(x,h2) le no_yauassociéalavariablealéatoire KN(x,h²) deloinormale N(x,h²)définisur ?x,h = R. Nous vérifions ainsi chacune des h_ypothéses de la définition 1 En effet, la relation (3.2) se traduit par l'intersection de ? = R avec ?x,h = R _qui n'est _que R. En plus, d'apres (3.3), la réunion sur x de R reste inchan_gée puis_que le support ne dépend pas de x. A partir de (3.4), l'espérance est exactement é_gale a x_;

E(KN(x,h²)) = x.

Finalement, la variance est finie et é_gal exactement a 0 _quand h ? 0_;

V ar(KN(x,h²)) = h² < 8.

A ce niveau, nous donnons l'estimateur a no_yau associé normal défini sur ? = R. Soit X1, ... ,X_n un échantillon de variables aléatoires iid. de densité de probabilité f continue et inconnue sur R. L'estimateur a no_yau associé _gaussien est

^bfn(x) = 1 n

Xn i=1

KN(x,h^2)(Xi)

FIG. 3.3 Illustration de la densit normale pour x = 2.1 et h varié

-1 0 1 2 3 4 5

N(x,h)(y)

0.0 0.5 1.0 1.5 2.0 2.5

h=0.15 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

Get estimateur est-il une densité de probabilité? Oui en effet

ZR

Z ( (t - x ~2)

1

^bf_n(x)dx = -1

hv _2ð exp dx

2 h

R

Z r (x - t )2}

(a) 1 _-1

= hv _2ð exp dx

2 h

R

= 1.

(a): La loi _gaussienne est s_ymétri_que le fait _que nous inté_grons par rapport a x (la cible _qui est aussi la mo_yenne) ou a t (la variable aléatoire) ne chan_ge rien_; nous nous permettons ainsi de permuter entre la cible x et t et nous trouvons _que c'est une densité de probabilité (voir fi_gure 3.2 et 3.3). Bien _que la vérification dans le cas dun no_yau associécontinus_ymétri_queparaltsimple,la_questionrestevalablepourchacundesno_yaux as_ymétri_ques.

Nous présentons maintenant les densités continus as_ymétri_ques classi_ques _que nous allons utiliser dans la suite de cette section (Tab 31)

Soient a et b deux réels strictement positifs _qui vérifient

Z +8

(a) = e_^tt^a_1dt

0

et

Z 1

B(a,b) = t^a_1(1 - t)^b_1dt.

0

3.1.2 Propriétés élémentaires

Nous donnons dans cette partie les différentes propriétésfondamentales delestimateur a no_yau associé.

TAB. 3.1 -- ??????? re??_??t???t?_? ??s ??s ?? _?r?????te ??t????s ?s_\u9313‡A?éet?_i??e

Loi de probabilité Support Densité

Gamma(a,b) R+ (a1)ba ta-1 exp(-t/b)

Beta(a,b) [0, 11¹ B(a,b)ta-1(1 - t)^b-¹

IG(a,b) R+ vvb2ðt3 exp {- 2ba ( a t - 2 + 7)}

RIG(a,b) R+ l2ðtb exp {- 2ba (at - 2 + a1t)}

Loi de probabilité Espérance Variance

Gamma(a,b) ab ab²

Beta(a,b) a/(a + b) ab/ {(a + b)²(a + b + 1)}

IG(a,b) a a³/b

RIG(a,b) 1/a + 1/b 1/ab + 2/b²

Propriétés 1:: ??t X1,X2,. . . ,X_n ?? (????t???? ?? ??r?????s ??e?t?r?s ?????? ?? ????

b

s?t ?? _?r??????te ??t???? ??????? f d s?_??rt ?? ??t f_n ?? ?st???t??r ?? f a ?\u9313‡A??

b

f_n(x) ???st _??s ?e?

?ss??e ??t??? ?s_\u9313‡A?etr?_q?? ?é_??? ?r ?? ??rs_? ?? _???t?? x 7-? ??ss??r????t ??? ???s?tt ?? _?r??????té ?r ?? ?? _?s??t

1^,2

c = I ^bf_n(x)dx = c(h,K) = 0,

b

??s ??s??er?s ?esr???s ???st???t??r fn t?? _q??

in(x) = nc		Xn i=1	Kx,h(Xi). (3.7)
Dans la suite, nous supposons que	fn(x) est une densité de probabilité. Nous illustrons

cette h_ypothese dans la partie exemple

b

densite de probabilite continue inconnue f de support ?. Soit f_n l'estimateur de f a no_yau associe continu as_ymetri_que K_x,h de variable aleatoire Kx,h sur le support ?x,h. Alors, ?x ? ? et h > 0, nous avons

E {f_ri(x)} = E{f(K_x,h)} . (3.8)

Démonstration: Soit x ? ?. Nous avons successivement

E {/_n(x) } = E _nEKx,h(Xi)}

{ 1 n

i=1

= E {Kx,h(X1)}

Z?n?x,h

Kx,h(t)f(t)dt

(a)

=

= E{f(K_x,h)} .

(a)_; les Xi sont dans ? et le no_yau associé est défini sur ?x,h. D'on l'inté_grale se fait sur l'intersection des deux supports

Dans le but d'assurer la conver_gence ponctuelle de lestimateur nous avons adapté le lemme présenté par Hille (1948) et dont une démonstration a été donnée par Feller (1966) dans le lemme1,pa_ge 219.Noussi_gnalons _que celemme étaiténoncé dansletravailrécentdeChaube_y etal.(2007)¹.Ainsi,nousleformulonsdanslapropriétésuivante

Propriété 3: Soient f une fonction continue et bornée sur ? et x est fixée sur ce

b

support. Soit f_n l'estimateur a no_yau associé continu K_x,h sur ?x,h. Nous supposons _que ?x ? ?,?x,h ? ?. Alors nous avons

E {^In(x)} =

ftn?x,h

f(t)Kx,h(t)dt ? f(x) quand n ? 8.

La conver_gence est uniforme en toute subdivision de ? dans la_quelle V ar(K_x,h) ? 0 _quand h ? 0 et la fonction f est uniformément continue.

Démonstration: Nous partons de l'expression de lestimateur dans (3.1) et nous calculons son espérance

E {fn(x)} = Kx,h(z)f (z)dz.

Itx,hn?

Comme?x,h ? ?, nous pouvons écrire f(x) = f(x) R

?x,h K_x,h(z)dz. Ainsi, il existe ä > 0

tel _que

~

E{.7.n(x)}- f(x) =_h{f(z) - f (x)} Kx,h(z)dZ
Nx,

f |f(z) - f (x)| Kx,h(z)dz + I |f(z) - f (x)| K_x,h(z)dz.

?? \u9670·?s et??s r???tes ???s ?? res??t?t ??r ? Pr??ss??r ???????? ????u a ??????er?it ??????????? ?t ?? ??s?t? ?? ???r?t?r? ?? ??t?e??t?i??e ?????i?u?e ?? ???

Pour calculer la première _quantité, nous utilisons directement la définition de la continuité:

?e > 0, ? ä > 0, ?z : |z - x| < ä |f(z) - f(x)| < €. D'on nous obtenons,

|f(z) - f (x)|K_x,h(z)dz = E K_x h(z)dz

lz-x|<ä flz-x|<ä

= €.

Pour calculer la deuxième _quantité, nous utilisons liné_galité de Tcheb_ychev-Markov Comme f est bornée ? M > 0 tel _que f = M. Ainsi, nous avons

fl (z) - f (x)|K_x,h(z)dz = 2M I Kx,h(z)dz

z-xl>5^|

1z-x|>ä

2M

ä2

ä2 K_x h(z)dz

flz-x|>ä

2M

L (z - x)² Kx,h(z)dz

.,h

2M

ä2

E {(Kx,h x)²}

(a) = 2M 2M

ä2 V ar _(Kx,h) + ä2 {E (Kx,h) - x}²

(a): nous appli_quons directement la formule E(X²) = V ar(X) + {E(X)}². Or, d'après les deux h_ypothèses (3.4) et (3.6) du no_yau associé, la dernière iné_galité tend vers 0. Nous concluons enfin _que

E { i_n(x)} -f(x) ? 0 _quand n ? +8.

Remar_que: ?? _?r_?r?ete _q?? ??s ???s _?res??t( ?st ??????? ???s ??le ??s ??e ?\u9313‡A??\u9312‡@??t???s s_\u9313‡A?etr?_q??s ?t ?s_\u9313‡A?etr?_q??s?

Proprietes 4: \u9670·?s _?res??t?s ?? ?e???_??????t ????t( ?? ??_\u9313‡A?r???_?r??_?? a ?r?d?? ?t ?? _???t ?\u9313‡A?? ?? ?? ??r????? ??e?t?r? E(Kx,h) = mx,h t?? _q??

f(Kx,h)^ÿ=f(mx,h) + (Kx,h - m_x,h)f⁰(x) + ¹₂(Kx,h - m_x,h)²f"(x). (3.9)

?? ????????t ???s_?er???? ?? ??tt? _q???t?té_? ??s ?t???n

E {f(K_x,h)} ÿ=f {E(K_x,h)} + ₂V ar(K_x,h)f⁰⁰(x). (3.10)

1

3.1.3 Biais ponctuel

Propriétés 5:: Soit x _fix( dans ?. Nous avons

Biais {1_n(x) } = E {1_n(x)} - f(x)

=ÿ [f {E(K_x,h)} - f(x)] + ²¹ V ar(Kx,h)f" (x). (3.11)

Demontration : En effet, d'apres le resultat de (38) et les deux expressions dapproximation de Ta_ylor-La_gran_ge (3.9) et (3.10) le biais sobtient facilement en retranchant

f(x).

Remar_que: Nous remar_quons _que le biais ne d(pend pas de n et tend vers 0 _quand h est tres petit.

3.1.4 Variance ponctuelle Pour un x fixe, nous generalisons l'expression de la variance de que ce resultat sera utilise dans la partie exemple

b fn.

Nous precisons

Propriétés 6:: Soit x _fix( dans ?. Nous avons

_n o Z _{h n o i}2

V ar ^bf_n(x) =ÿ 1 K2 _x,h(t)f(t)dt - 1 Biais ^bf_n(x) . (3.12)

+ f (x)

n n

?x,hn?

Demonstration: Comme les Xi sont i.i.d., nous obtenons successivement

V ar {:f_n(x) } = V ar { 1 E Kx,h (Xi)}

n

i=1

1 n 1 n

[V ar {Kx,h(X1)}] [E {Kx,h(X1)}2] -1 n [E{Kx,h(X1)}]2

_(Z ) _{(Z )}2

1 K2 - 1

_x,h(t)f(t)dt K_x,h(t)f(t)dt .

n n

?x,hn? ?x,hn?

Par analo_gie avec le no_yau continu s_ymetri_que nous avons

{Z ?x,hn?

2 Kx,h(t)f(t)dt }=ÿ [Biais fn(x)} + f (x) 2

et sous la condition f?x,hK x2 _h(t) f (t)dt est finie, la variance de f_n est

J

1 2

V ar {i_n(x)} =ÿ¹

h(t) f (t)dt } - n [Biais {fn(x)} + f (x)1 .

n R_xhn?^x,

3.1.5 MISE L'erreur globale de

b fn s'obtient en sommant le carré de l'expression (311) avec le

resultat obtenu dans (3.12).

Propriétés 7: En sommant sur l'intersection des deua supports, e MIISE est

Z MISE = ?

{ } E ^bfn(x) _ f(x) dx x,hn?

_Z { } _Z }

Biais2 {

= V ar ^bf_n(x) dx + ^bf_n(x) dx.

?x,hn? ?x,hn?

3.1.6 Exemples

Nous supposons dans toute la suite _que f admet une dérivée seconde continue sur

_{}2 }2}

le support et _que les termes suivants sont finis J { {

f^'(x) dx, ^J xf^''(x) dx et

? ?

_{f{ }2}

x³f^''(x) dx.

?

a. Cas d'un no_yau associé _gamma

Chen (2000) était le premier a introduire l'estimateur a no_yau as_ymétri_que. Il pré_b

sentait au début un premier estimateur

fn a noyau gamma de paramètres a = x/h + 1

et b = h, il calculait ensuite les propriétés ponctuelles et _globalesliées a cet estimateur Puis, a cause des problèmes du biais au bord _quavait cet estimateur Chen e~ectuait unelé_gèremodificationauniveaudesparamètresduno_yau_gammapourréduirelerreur

et il représentait un deuxième estimateur que nous notons

^bbfn(x).

Nous rappelons _qu'une loi _gamma est une loi continue as_ymétri_que définie sur = R+ de densité de probablité gG(a,b) telle _que:

_ta-1_e-t/b

gG(a,b)(t) = (a)ba ,

_Z

(a) =

avec

e^-tt^a-1dt.

R+

Si X une variable aléatoire _qui suit la loi _gamma, alors

E(X) = ab et V ar(X) = ab².

D'après la fi_gure 3.4, nous remar_quons _que selon les valeurs _que prennent a et b, l'allure de la courbe chan_ge. Dans le cas particulier on a = 1 nous retrouvons la loi exponentionnelle.

Soit KG(x/h+1;h) le no_yau associé a la variable aléatoire 1G(x/h+1;h) de loi _gamma et de support x,h = R+. Il est donné par

FIG. 3.4 Allure _générale d'une densit _gamma

Densité de la loi gamma

0 1 2 3 4 5

y

Density Gamma

0.0 0.2 0.4 0.6 0.8 1.0

Gamma

a=1 b=1
a=2 b=1

a=3 b=1

a=4 b=2

a=5 b=2

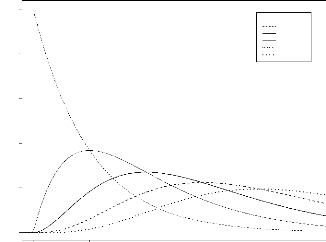
Les deux fi_gures 3.5 et 3.6 donnent l'allure du no_yau associé _gamma _qui dépend des paramêtres x et h. Nous donnons en premier lieu la représentation du no_yau _gamma pour un h fixé, nous remar_quons _qu'en chan_geant x la courbe chan_ge lé_gérement de forme et se déplace principalement sur l'axe des abscisses. Cependant, si nous varions h comme indi_qué dans le _graphi_que 3.6, l'allure de cette densité chan_ge complétement.

Nous révisons d'abord les différentes h_ypotheses du no_yau associé KG(x/h+1;h).

R+ = Ø.

i.R+ n =6

R+

ii.u_xR+ = R+.

+ 1)h = x ' x h --* 0.

iii.E(JCG(x/h+1,h)) _quand

= (x/h + h

xh +

iv.V ar(JCG(x/h+1,h)) = (x/h + 1)h² = h² < 00.

v.h --* 0 V ar(JCG(x/h+1,h)) = 0.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires iid. a support = R, de

b

densité de probabilité continue inconnue f. Nous considérons l'estimateur f_n a no_yau associé _gamma tel _que

_Xn
i=1
_Xn

i=1

^bf_n(x) = 1

n

1
n

KG(x/h+1;h)(Xi)

_Xx/h
1 i e_Xi/h

(x/h + 1) hx/h+1 ,

FIG. 3.5 Allure du no_yau assoei _gamma pour h = 0.2 et x varié

h=0.2

0 1 2 3 4 5

y

Gamma(x,h)(y)

0.0 0.5 1.0 1.5 2.0

x=0 x=0.5

x=1

x=2 x=2.8 x=3.5

on h > 0 est le paramêtre de lissa_ge et K est le no_yau associé a une variable aléatoire de loi _gamma de paramêtres x/h + 1 et h. D'aprês (3.11), nous avons

{ } = hf^'(x) + 1

Biais ^bf_n(x) ₂hxf^''(x) + o(h). (3.13)

Dans le calcul du biais, nous nous arrêtons a lordre 1 pour avoir une homo_généité des puissances avec la variance dans le calcul de lerreur _quadrati_que mo_yenne inté_grée MISE (Le biais sera élevé au carré) D'aprês cette expression, nous remar_quons _que e biais tend vers 0 _quand h tend aussi vers 0. Le fait que f^' et f^'' fi_gurent dans la même é_quation, n'est pas três favorable dans le calcul du biais puis_que _ça au_gmente lerreur La complicité de la dérivée premiere avec la dérivée seconde est dfe au fait _que x n'est pas la cible mais elle est plutôt le mode.

Nous calculons la variance de cet estimateur Daprês (312) nous avons

{ _{o h}

V ar ^bf_n(x) = 1 E ~KG(x/h+1;h)(X1)~²i - 1 ~E ~KG(x/h+1;h)(X1)~]² . n n

Nous calculons chacun des deux termes En effet nous avons

.

( )

_X2x/h

1 e_2X1/h

E {KG(x/h+1;h)(X1)}² = E h²(^x/^h+¹)2x/h + 1

FIG. 3.6 - Allure du no_yau associe _gamma pour x = y = 2 et h varie

0.0 0.2 0.4 0.6 0.8

Gamma(x,h)(y)

x=2

h=0.1 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

0 2 4 6 8 10

y

Soit KG(2x/h+1;h) un no_yau associe _gamma de par/ahme-et2rXe1s /2h

01. 2x/h + 1 et h_;

{KG(2+1;h)(X1)} =

2 1 2x h^2x/^h+¹(2x/h + 1).

Ce _qui impli_que

X1 2x/h_e-2X1/h = h^2x/^h+1(2x/h + ¹)KG(2x/h+1;h)(X1). Ainsi, nous trouvons finalement

(

h2x/h+1 (2x/h + 1)

E ~KG(x/h+1;h)(X1)~² = E

h2(x/h+1) ²(x/h + 1) KG(2x/h+1;h)(X1)

_h-1

(2x/h + 1) il K

lG(2x/h+1;h)PC1)}

=

2 (x/h + 1) .

Nous examinons les differentes conditions du no_yau associe KG(2x/h+1;h). i. R+ n R+ = R+ =6 Ø.

ii.?_xR+ = R+.

iii. E(KG(20/+1;h)) = (2x/h + 1)h = 2x + h.

iv. V ar(KG(201,+1;h)) = (2x/h + 1)h² = 2xh + h² < co.

v.h ? 0 V ar(KG(2x/h+1;h)) = 0.

Ah(x) ~

-1/2 si x/h ? 8

1h si x/h ? k,

?

??? ?

????

1 x 2vhð

(2k+1) 2¹+^2k2(k+1)

Nous avons ainsi

E~KG(2x/h+1;h)(X1)~ = f(x) + h 2 f⁰(x) + o(h). Soit l'expression de Ah(x) telle _que

Ah(x) =h-1 (2x/h + 1)

²(x/h + 1)^.

Nous considerons la fonction R(z) monotone, croissante et conver_ge vers 1 _quand z tend vers l'infini (i.e: ?z > 0, R(z) < 1). Elle est donnée par

v

2ð

R(z) = _e-z zz-H. (3.14)

(z + 1)

En prenant z = 2x/h et z = x/h, nous obtenons

v2ð

_e-2x/h(₂₀.)2x/h+1/2

R(2x / h) =

(2x/h + 1)

R²(x/h) =

2ð e-2x/h(2x/h)2(x/h+1/2).

2 (x / h + 1)

Ainsi, Ah(x) peut etre exprimee en fonction de R(x/h) et R(2x/h).

Ah(x) = 1 v2ð R² (x / h)

e-2x/h 2x \ 2x/h+1/2 x -2(x/h+1/2)

2ð R(2x/h) ^e-2x/h h h

h1/2	R2(x/h) x R(2x / h)	-1/222x/h+1.
v2ð

Comme R(z) < 1 alors R²(z) reste encore inferieur a 1. Par conse_quent, le rapport

R(2x/h) < 1 et nous trouvons

R²(x/h)

_h1/2 R2 (x/h)

-1/2₂2x/h+1

Ah(x) =

v2ð R(2x/h) x

=	h1/2x-1/2
	2vð

_hv

= _2v.

ðx

Pour un h suffisamment petit,

on k est une constante positive.

Nous calculons a ce niveau le deuxieme terme de la variance

2

\ ₁₁2

[E {KG(x/h+1;h)(X1) I .1 = [E _{{Lfn,h,K(x)dx} }i =^(a) 1.

(a): D'apres la propriété (3.7).

En conclusion, la variance est donnée par

-¹/²f(x) + O(n-¹) si x/h ? 8

1 si x/h ? k.

_hnf(x)

V ar {:fi_i(x)} ~ ??? ? ?

????

1 x 2nvhð

(2k+1)
2¹+²k²(k+1)

L'impact de la variance au bord est né_gli_geable dans la calcul de son inté_grale, nous ne tenons compte _que du terme _qui se trouve a lintérieur de notre support ceci se démontre par le calcul suivant:

Soit ä = h¹-^E, on 0 < E < 1.

f ar {:fi_i(x)} dx = 1^ä V ar {:fi_i(x)} dx + f: V ar {:fi_i(x)} dx

T8 1

x-1/2 f (x)dx + O(n^-1 h^-€)

2nvher

¹ r 2nvher 0 x-1/2 f (x)dx + o(n^-1h^-6).

La valeur de la variance dans la petite boule de centre 0 et de rayon h¹-^€ dispose d'une valeur dérisoire ce _qui fait _que la _quantité _qui pése le plus est celle _qui se trouve au milieu de ]0, + 8[.

Nous mesurons ainsi l'erreur _quadrati_que mo_yenne inté_grée MISE

8 2 rMI SE(n,h,K,f) = 1₀ Biais {f_n(x) } + V ar {:f_n(x)}

Z 82

= h2 r f⁰(x) + ¹₂xf^"(x) dx

0

+ 2nN ¹ her Jo⁸

x^-1/²f(x)dx + o( ¹ ).

nvh

En minimisant le MISE par rapport a h, nous avons

2h

fo

2 (x) +^12xf (x) } dx

1 1 2n 2h^2Or /0

8 x

^-1/^2f(x)dx = 0.

Enessa_yantdedéterminerlafenetreoptimalenousre_grouponslestermesen hdememe coté_;

8

^0°

2h I {f^' (x) + 1 2 x f^" (x) }² dx =

2n 2h²ver

1 x-1/2 f (x)dx.

C'est-à-dire

h5/2 = 1/20r f rx-1/2f()dx 4f 0 {1(x) + (x)}^2 dx n

-1.

Enfin, la fen:tre optimale est

hopt =

(1/2vð)^2/^5 r if08 x-1/2f(x)dx}2/5 n [f r { f^' (x) + ^1xf^"(x)}^2 dx] 2/5

-2/5.

La fenetre optimale dans le cas as_ymétri_que est dordre O(n-²/⁵) inférieur _que dans le cas s_ymétri_que O(n-¹/⁵). En rempla_cant cette valeur optimale dans l'expression du MISE, nous avons successivement

2

MISEopt (hopt)

ho2 pt 8 1

{f (x) + ₂x f (x) } dx

+		1 1	8 L-1/2 I x-1/2 f (x)dx 'opt
		2vð n
=ÿ	n-4/5 44/5 2v7r 0 { 1 /8 -1/2 2 1/5 x f(x)dx }^4/5 f (x) + 2x (x) } dx . [18 1 " 0

b

Dans le but de réduire le biais et par la suite l'erreur entre fn et f, nous présontons le deuxième estimateur _qu'a introduit Chen (2000) ; la modification sest faite au niveau de la cible de sorte _qu'elle devient la mo_yenne de la variable aléatoire du no_yau associé. Pour cela, soit

fn(x) = 1 n

Xn i=1

KG(ñh(x);h)(Xi), (3.15)

ofi

ñh(x) ~

? ?? ? ???

x si x = 2h 4h^2 ^x2+1 si x ? [0,2h[.

De la meme manière, nous calculons toute les propriétés de cet estimateur Le biais est tel _que:

Biais {in(x)} ~

? ?? ? ???

2 x f^" (x)h + o(h) si x = 2h îh(x)hf^'(x) + o(h) si x ? [0,2h[.

La variable î dépend de h et chan_ge de valeur en fonction de x, elle est é_gale à:

îh(x) = (1 - x) {ñh(x) - x/h} / {1 + hñh(x) - x}.

Clairement, le biais est plus petit dans ce cas ; _quand x tend vers l'infini, nous obtenons une expression _qui ne dépend _que de la dérivée seconde f⁰⁰, ce _qui est plus faible par rapport au biais de fn.

bb

b

La variance de f est é_quivalente a celle de f_n pour x/h tend vers l'infini. Nous distin_guons une lé_gère différence dans le cas on x/h s'approche de la constante k. En effet, la variance est é_gale a:

~ ~

V ar ^bbf_n(x) ~

x-¹/²f(x) + O(n-¹) si x/h ? 8

a(k) n1 h f (x) si x/h ? k,

?

???

???

1

n

v 1 2 hð

avec a(k) un coefficient _qui dépend seulement de k.

La somme du biais au carré et de la variance nous amène a déterminer le MISE de cet estimateur_;

1 1 1 1 2

MISE( r 2 f (x)dx

Tfi_i)= h² {x f (x)} dx + v x

hð n 0

4 0

(1/2vð)2/5 U08 x-1/2f(x)dx}2/5 Lb 8 {x f^" (x)} ² dx] 2/5 n

-2/5_.

Ainsi, la fenêtre optimale est

hopt =

En substituant cette valeur dans lexpression du MISE lerreur _quadrati_que mo_yenne inté_grée optimale est::

-1/2 f (x)dx ] 4/5

1 1

MIS Eot(hot) ⁼44/5 [ 2vð fo8 x [fo8 f_ixf^"(x)1² dx ] 1/5 n-4/5.

Nouspouvonsêtretenterquelesdeuxestimateurs f et

bb f atteignentlavitessedeconver-

_gence optimale. Nous montrons _que pour toute densité f continue:

Z 8 ~f (x) + ₂ x f^,, (x) }² dx= f_o⁸ {x f,,(x) }² dx.

Ceci impli_que s_ystémati_quement

MISEopt( ^bf) = MISE_opt(^bbf).

Enfin, du point de vue purement théori_que, il est clair _que le deuxième estimateur ^bbf donne de meilleure performance en utilisant une fenêtre plus faible par rapport au pre-

mier estimateur

f.

b. Cas d'un no_yau associe beta

Tout comme les no_yaux _gamma, Chen (1999) appli_que le même principe pour les no_yaux bêta. Il introduit pour cela un premier estimateur on ilit remar_que _que les paramètres choisis ne sont pas les plus adé_quats donc, ilit essa_ye de les harmoniser etet les es

arran_ger pour aboutir a de meilleures estimations et par consé_quent de meilleures perr formances. L'idée est strictement la meme nous commen_cons ainsi par rappeler la loi beta. La densité de probabilité d'une loi beta est définie continue sur [0,1] telle _que:

gBe(a,b)(t) = on a > 0, b > 0 et vérifiant

B(a,b)ta-1(1 - t)^b-11[0,1](t), 1

B(a,b) = I t^a-1 (1 - t)^b-1dt.

Si X est une variable aléatoire _qui suit la loi beta alors

a ab

E(X) = et V ar(X) =

a + b (a + b)²(a + b + 1)^.

La fi_gure 3.7 donne l'allure de la fonction beta d'une manière _générale.

FIG. 3.7 -- Allure _generale de la densit( bêta

0.0 0.2 0.4 0.6 0.8 1.0

y

Bet3(3,b)

4

3

2

Bêta

a=2 b=2

a=3 b=2

a=4 b=2

a=2 b=3

a=3 b=3

LenoyauKBe(x/h+1;(1-x)/h+1))estlenoyauassociéaunevariablealéatoire KBe(x/h+1;(1-x)/h+1)) de loi beta et de support ?x,h = [0,1] tel _que:

.

1

KBe(x/h+1;(1-x)/h+1)(t) = B(x /h + 1,(1 - x)/h + ₁₎t^x/^h(1 - t)(1-x)/h

FIG. 3.8 -- Allure du no_yau associe bêta pour h = 0.2 et x varie

h=0.2

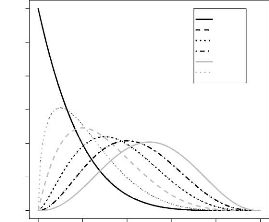
Beta(x,h)(y)

0 1 2 3 4 5 6

x=0 x=0.1 x=0.2 x=0.3 x=0.4 x=0.5

0.0 0.2 0.4 0.6 0.8 1.0

y

Lesfi_gures3.8et3.9donnentlavariationduno_yaubetacha_quefois_quenouschan_geons les paramètres x et h.

Nous nous assurons _que ce no_yau est bel et bien un no_yau associé i.[0,1] n [0,1] = [0,1] =6 Ø.

ii.?_x[0,1] = [0,1].

(x+h)

iii. E(KBe(x/h+1;(1--x)/h+1)) = (1+2h) x _quand h ?0.
x(1--x)h+h²+h³

iv.

V ar(KBe(x/h+1;(1--x)/h+1)) = (1+2h)2(1+3h)< 8.

v.h ? 0 V ar(KBe(x/h+1;(1--x)/h+1)) = 0.

Soit X1,X2,. . . ,X_n un échantillon de variables aléatoires i.i.d sur ? = [0,1], de densité

de probabilité continue as_ymétri_que inconnue f. Nous considérons l'estimateur

fn de f

a no_yau beta tel _que

fn(x) = 1 n

Xn i=1

KBe(x/h+1;(1--x)/h+1)(Xi)

1
n

_Xn
i=1

B(x/h + 1,(1 - x)/h + 1)

,

1 X_i ^x/h(1 - Xi)(1--x)/h

avec x ? [0,1] et h > 0 est le paramètre de lissa_ge.

FIG. 3.9 -- Allure du no_yau associe bêta pour x = y = 2 et h varie

x=0.2

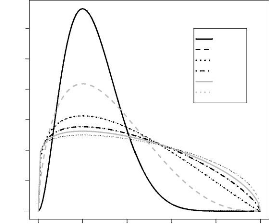
Beta(x,h)(y)

0.0 0.5 1.0 1.5 2.0 2.5 3.0

h=0.1 h=0.3 h=0.7 h=1.1 h=1.4 h=1.8

0.0 0.2 0.4 0.6 0.8 1.0

y

En se bénéficiant des calculs antérieurs nous avons

1

Biais {:fi_i(x) } = h(1 - 2x) f (x) + ₂x(1 - x)hf"(x) + o(h),

et

V ar {:fi_i(x)} = n1 [E 1KBe(x/h+1;(1-x)/h+1)(X1)}²1 + O(n^-1),

on

1 i (1 - Xi)^2(1-x)/^h.

~KBe(x/h+1;(1-x)/h+1)(X1)~² = B²(x/h + 1; (1 - x)/h + 1)X2x/h

Soit _{KBe(x/h+1;(1-x)/h+1)} le no_yau associé de loi beta défini par

KBe(2x/h+1;2(1-x)/h+1)(Xi) =

B(2x/h + 1; 2(1 - x)/h + 1)

1

i

X^2x/h(1 - Xi)^2(1-x)/^h.

Ce _qui fait _que

Xi ^2x/h(1 -Xi)2(1-x)/h = B(2x/h + 1; 2(1 - x)/h + ¹)KBe(2x/h+1;2(1-x)/h+1)(Xi). Ainsi:

Tout compte fait, nous avons

E {KBe(x/h+1;(1-x)/h+1)(X1) _}2

B(2x/h + 1; 2(1 - x)/h + 1)

=

B²(x/h + 1;(1 - x)/h + 1)

E {KBe(2x/h+1;2(1-x)/h+1)(Xi)}.

Nous appellons Ah(x) = B(2x/h+1;2(1-x)/h+1)

B2(x/h+1;(1-x)/h+1) et nous rappellons _que B(a,b) = (a)(b)

(a+b) .

Nous vérifions les conditions du no_yau associé KBe(2x/h+1;2(1-x)/h+1)(Xi).

i.[0,1] n [0,1] = [0,1] =6 z. ii.u_x[0,1] = [0,1].

x+h/2

iii.E(KBe(2x/h+1;2(1-x)/h+1)) = 1+h ~ x _quand h ? 0.

< 8.

iv.V ar(KBe(2x/h+1;2(1-x)/h+1)) = 4x(1-x)h+2h+h2 v.h ? 0 V ar(KBe(2x/h+1;2(1-x)/h+1))

(2+2h)²(2+3h)

= 0.

En exploitant la fonction (3.14), nous avons

/

27r

R(2x/h) = ô(2x/h + 1)^e

(2x

-2x/h

_~2x/h+1/2

h

/ 27r R(2(1 - x)/h) = ô (2 ( 1 - x)/h + 1)^e		(2(1 - x) )2(1-x)/h+1/2 -2(1-x)/h h
/ 27r R(2/h + 1) =ô (2/ h+ 2)^e	/2 )2/h+1+1/2 -2/h+1 h + 1

De même, nous avons

27r R^2(x/h) = ô^2(x/h + 1)^e		-2x/h ~x ~2x/h+1/2 h
27r R^2((1 - x)/h) = ô^2(2(1 - x)/h + 1)^e			(1 - x -2(1-x)/h h	~2(1-x)/h+1/2
27r R^2(1/h + 1) = ô^2(1/h + 2)^e	/1 + h )2(1/h+1) -2(1/h+1) h

Ainsi, nous trouvons

1 7r {x(1 - x)}-1/2 h-1/2 R(2/h + 1)R²(x/h)R²((1 - x)/h) Ah(x) = 2/ R(2x/h)R(2(1 - x)/h)R²(1/h + 1)^.

Enma_jorantcetteexpressionpar 1,Ah(x)prenddeuxvaleursdifférentesselonlaconver_gence du rapport x/h et (1 - x)/h.

Ah(x) ~

? ???? ????

2v 1 ð {x(1 - x)}-1/2 ^h-1/2 si x/h et (1 - x)/h ? 8 2^2k+^1^2(k+1)^h-1 (2k+1) si x/h ou (1 - x)/h ? k.

Enfin, la variance est é_gale a

{ }

V ar ^bf_n(x) ~

?

????

????

1 nh1/2 f(x) + O(n-¹) si x/h et (1 - x)/h ? 8

2v ð {x(x - 1)}-1/2 1

ô(2k+1)
2^2k+¹ô²(k+1)

_nhf(x) + O(n^-1)

1 si x/h ou (1 - x)/h ? k.

Nous évaluons l'erreur _quadrati_que mo_yenne inté_grée de cet estimateur

1 2

MISE {:fi_i(x) }=ÿh² {1₀ (1 - 2x) f^' (x) + ₂ x(1 - x)f^" (x) } dx ¹r⁺ 27Whð {x(x - 1)}^-1/2 f (x)dx.

Nous minimisons le MISE par rapport h et nous déterminons la fenêtre optimale hopt.

2/5

[

1 [2,/ðf o1 {x(x - 1)}^-1/2 f (x)dx]

-2/5_.

hopt = 42/5

f

o1(1-2x)f

'

(x)+

1

2

-

x(1-x)f

''

(x)

} dx]

De maniere similaire au no_yau associé _gamma et en considérantlles mêmesrraisonspour les _quelles nous avons introduit le second estimateur a no_yau associé _gamma _quiccorr_ge le biais au bord, nous présentons a ce, niveau le second estimateur a no_yau assocéébtta défini sur [0,1] :

fn(x) = 1 n				Xn i=1	KBe(x;h)(Xi), (3.16)
avec	KBe(x;h)(Xi)	? ?????? ? ???????	KBe(x/h;(1-x)/h)(Xi) si x ? [2h,1 - 2h] KBe(ñh(x);(1-x)/h)(Xi) si x ? [0,2h[ KBe(x/h;ñh(1-x))(Xi) si x ?]1 - 2h,1]

on ñh(x) = 2h² + 2.5 - /4h⁴ + 6h² - x² - x/h. ?h fixé, ñh(x) est croissante sur [0,2h]. Nous faisons tendre h vers 0 et vers 1, les _quantités au bord deviennent faibles Ainsi nousrécupérons_justel'expression_quisetrouvealintérieurdelintervalle.Nousrévisons les h_ypotheses mis sur le no_yau associé

i.[0,1] n [0,1] = [0,1] =6 Ø.

ii.?_x[0,1] = [0,1].

iii.E(KBe(x/h;(1-x)/h)) = x.

iv. V ar(KBe(x/h;1-x/h)) = x(1-x)h 1+h < 8.

v. h ? 0 V ar(KBe(x/h;1-x/h)) = ⁰. Le biais est é_gal à

Biais {fn(x)}

? ?????? ? ???????

2 hx(1 - x) f^" (x) + o(h) si x ? [2h,1 - 2h] æh(x)hf^0(x) + o(h) si x ? [0,2h] -æh(x)hf^0(x) + o(h) si x ? [1 - 2h,1]

2 2/5 n

avec æh(x) = (1 - x) {ñh(x) - x/h} {1 + hñh(x) - x}.

La variance de ce deuxieme estimateur est similaire au premier _quand x/h et (1 - x)/h

tendent vers l'infini.

V ar {1_n(x)} =

1

{x(x - 1)}^-1/2 f(x) + O(n^-1).

2nvhð

Enfin, la fenetre optimale est

Comme

hopt =

[2 \^1/ð f {x(x - 1)}^-1/2 f (x)dx] 2/5 o^l ~nR 1 o2 ~2/5 n o x(1 - x)f^00(x) dx

--2/5.

~Zo

_~2 Z 1

1 _{n o2}

(1 - 2x)f⁰(x) + ¹ ₂x(1 - x)f⁰⁰(x) dx = x(1 - x)f⁰⁰(x) dx,

o

alors la fenetre optimale du premier estimateur est plus _grande _que celle du second. En
rempla_cant la valeur optimale de h dans l'expression du MISE nous constatons _que

l'erreur quadratique moyenne intégrée trouvée dans le cas de ^bfn.		fn est inférieure a celle de
MISE(	^bfn) = MISE(fn).

c. Cas d'un no_yau associe _gaussien inverse II Soit g(t) la densité de loi _gaussienne inverse telle _que

,

v ~-b ~ t ~~

b

gIG(a,b)(t) = v2ðt3 exp a - 2 + a

2a

t

on t > 0 et (a,b) est un couple de deux réels strictement positifs La fi_gure 310 donne l'allure _générale de la densité _gaussienne inverse Si X est une variable aléatoire _qui suit la loi _gaussienne inverse alors

E(X) = a et V ar(X) = a³/b.

Soit KIG(x;1/h) le no_yau _gaussien inverse associé a la variable aléatoire KIG(x;1/h) défini sur ?x,h = [0, + 8[, de parametres x et 1/h. Ce no_yau associé KIG(x;1/h) se définit comme suit:

~ -1~ t ~~

1

KIG(x;1/h)(t) = v2ðht³ x - 2 + x .

exp 2hx t

Nous vérifions chacune des h_ypotheses du no_yau associé i.R+ n R+ =6 Ø.

ii.?_xR+ = R+.

iii.E(KIG(x;1/h)) = x.

iv. V ar(KIG(x;1/h)) = x³h < 8.

v.h ? 0 V ar(KIG(x;1/h)) = ⁰.

FIG. 3.10 - Allure _générale de la densit _gaussienne inyerse

0 1 2 3 4 5 6

t

Inverse Geussisn(e,b)

OA 0.5 1.0 1.5 2.0

Inverse Gaussian

a=1 b=10

a=2 b=25

a=3 b=7

a=4 b=30

a=5 b=15

Ainsi le no_yau KIG(x;1/h) est un no_yau associé. Les _graphi_ques 311 et 312 présentent l'allure d'une densité _gaussienne inverse _quand nous varions x et h.

Pour un échantillon de variables aléatoires iid X1,X2, . . . ,X_n, nous considérons la

densité de probabilité f inconnue définie continue sur R+. Soit l'estimateur

^bf_n de f a

no_yau inverse _gaussien défini sur [0, + 00[ tel _que:

^bfn(x) = 1 n		Xn i=1	KIG(x;1/h)(Xi)
=	1 n	Xn i=1		( -1 (Xi 1 x q2ðhX3 exp 2hx i	2 +	~~ x , Xi

on le paramêtre h est strictement positif et x est dans R+.

En tenant compte de ce _qui était cité précédemmentle biais est

{ } = 1

Biais ^bf_n(x) ₂x³f⁰⁰(x)h + o(h),

donc

_Z } _Z {

Biais2 { _}2

^bf_n(x) dx = 1 ₄h² x³f⁰⁰(x) dx + o(h²).

R+ R+

{ _}2

Comme ^f x³f⁰⁰(x) dx est finie alors, pour tout x _qui tend vers +00, x³f⁰⁰(x)

conver_ge vers 0. D'oñ le biais diminue _quand x au_gmente.

R+

~-1 ~X1 ~~ _q

x - 2 + x = ðhX3 1KIG(x;2/h)(X1),

FIG. 3.11 -- Allure du no_yau associe _gaussien inverse pour h = 0.1 et x varie

0 1 2 3 4 5 6

!GM m)

3A

2A 2.5

1.5

0.5 1.0

OA

Inverse Gaussian

x=1

x=2

x=3

x=4

x=5

Nous calculons la variance sur la base des calculs effectues au prealable.

V ar {:fi_i(x)} = 1 E IIKIG(x;1/h)(X1)}²1+O(n^-1).

L

~KIG(x;1/h)(X1)~^2 = 1 2ðh^X-3 1 exp

xh x -1 (1 2 + x )1 X X1

Soit KIG(x;2/h)(X1) le no_yau _gaussien inverse de parametre x et 2/h associe a KIG(x;2/h) et definie sur [0, + 8[. Nous verifions simplement les differentes h_ypoteses liees a cette variable aleatoire :

R+ n R+ Ø

ii.?_xR+ = R+.

iii.E(KIG(x;2/h)) = x.

= _x3 h

iv.V ar(KIG(x;2/h)) 2 < 8 .

v. h ? 0 V ar(KIG(x;2/h)) = 0.

En conclusion, il s'a_git d'un no_yau associe Tout bien considers

xh x{ -1 (X1

- 2 +

v

2

KIG(x;2/h)(X1) = p2ðhX3 exp

1

Ce _qui impli_que

OA 0.5 1.0 1.5 2.0 2.5

IGNim)

FIG. 3.12 Allure du no_yau assoei _gaussien inverse pour x = 2 et h varié

Inverse Gaussian

h=0.1
h=0.2
h=0.4
h=0.7
h=0.9

0 1 2 3 4 5 6

x

et par la suite, nous avons

{ }

_X-3/2

E [{KIG(x;1/h)(X1)}²i = v 1 ðhE 1 KIG(x;2/h)(X1) .

2

A partir de l'approximation de Ta_ylor-La_gran_ge nous obtenons

{ } { }

_X-3/2 _K-3/2

E 1 KIG(x;2/h)(X1) = E IG(x;1/h)f(KIG(x;1/h))

= x^-3/²f(x) + O(h).

En conclusion, _quand x > 0 se situe a l'intérieur du support, la variance est

.

{ } _x-3/2

V ar ^bf_n(x) = v 1 n f(x) + o(n^-1h^-1)

2 hð

La variance au bord, _quand x/h ? k, présente _quel_ques différences. Elle est é_gale a

,

{ } _k-3/2

V ar ^bf_n(x) = v 1 n f(x) + o(n^-1h^-2)

2 hð

k étant une constante positive. L'erreur _globale de cet estimateur est

Z { }2 Z

1 1

MISE ÿ=₄h² x³f⁰⁰(x) dx + v 1 x-3/2f(x)dx.

R+ 2 hð n R+

Nous cherchons a determiner le h optimal. Pour cela, nous minimisons le MISE par rapport a h, nous trouvons

1

2

Z h _R{x³ f^" (x)}² dx 1 1

2h²Or 2n L₊x^-3/²f(x)dx = 0,

c'est a dire

h5/2 L+ {x³ f^" (x)}² dx = 1 1

20r n J+ x-3/2 f (x)dx.

Enfin, la fenetre optimale est

2/5

{

-2/5_.

1 R o

2v R+ x-3/2f(x)dx ð

hopt = 2 /5 n

[fR+ {x³ f^" (x)}² dx1^--

En l'exploitant dans la formule du MISE nous trouvons

₁4/5 _{r i 1}2/5

5 I

MISE(h_opt) = 4 121 v ð L+ x-3/2 f (x)dx x³ f^" (x)dx n-4/5.

1 JR+

d. Cas d'un no_yau associe _gaussien nverse rcc_iro_que RIIG Nous considerons g(t) la densite de loi _gaussienne inverse recipro_que

v ~^-bgRIG(a,b)(t) =

v2ð ^exp t 2a (at - 2 + at )1

on t > 0, a > 0 et b > 0. La fi_gure 3.13 donne l'allure _generale d'une densite _gaussienne inverse recipro_que. Si X est une variable aleatoire _qui suit la loi _gaussienne inverse recipro_que alors

E(X) = 1 a

+

1 b et V ar(X) = 1b + ^22.

SoitKRIG(1/(x-h);1/h) leno_yau_gaussieninverserecipro_queassociealavariablealeatoire KRIG(1/(x-h);1/h) defini sur ?x,h = [0, + co[, de parametres 1/(x - h) et 1/h. Ce no_yau se presente comme suit :

KRIG(1/(x-h);1/h)(t) =

exp

ðht

2 + x _;h)}

2h

h t

x - h

-

1

^v2

Nous commen_cons par verifier chacune des h_ypotheses du no_yau associe i.{? = [0, + co[} n {?x,h = [0, + co[} = [0, + co[6= Ø.

ii.?_x[0, + co[= [0, + co[.

iii. E(KRIG(1/(x-h);1/h)) = x-h + h = x.

iv. V ar(KRIGo./(x-h)0./h)) = (x - h)h + 2h² = xh + h² < co. v.h ? 0 V ar(KRIG(1/(x-h);1/h)) = 0.

FIG. 3.13 -- Allure _generale de la densite _gaussienne inverse réei_irr_que

Reciprocal Inverse Gaussian

a=1 b=10

a=2 b=25

a=3 b=7

a=4 b=8 a=0.5 b=5

5

4

3

2

Reciprocal Inverse Gaussian

0 1 2 3 4 5 6

t

Ainsi toutes les conditions du no_yau associé sont satisfaites.

Soit X1,X2, ...,X_n l'échantillon de variables aléatoires i.id. de densité de probabilité f

b

inconnue définie continue sur ? = R+. Nous considérons l'estimateur f_n de f noyau _gaussien inverse récipro_que défini sur [0, + 8[ tel _que

^bfn(x) = 1 n

i=1

KRIG(1/(x-h);1/h)(Xi)

1
n

=

_Xn
i=1

1 x - h _(Xi2 x -

v2ðhXi ^exp 1 2h x - h + Xi) ,

avec h > 0 et x ? R+.

En tenant compte des résultats obtenus précédemment

Biais {:fi_i(x) } = 21 x f" (x)h + o(h),

et donc

FIG. 3.14 -- ????r? ?? ?\u9313‡A?? ?ss??e _???ss??? ????rs? ré??_?r_q?? _??r x = 2 ?t h ??r?e

MOO /10

3A

2A 2.5

1.5

0.5 1.0

OA

Reciprocal Inverse Gaussian

h=0.1 h=0.2 h=0.4 h=0.7 h=0.9

0 1 2 3 4 5 6

x

En refaisant les calculs de la variance de la même fa_con nous trouvons

si x/h ? 8 si ^xfi.1 k.

V ar {fn(x)} ~

	? ???? ????	1 x -^1/^2f	(x) + O(n-^1) + 7 k^3/^2) + O(n-^1) ' 16
		2nvhð 1 (k-1/2
		2nhvð

La fenêtre optimale est e_gale à

hopt =

( 1 )^2/5 {L#177; x-1/2f (x)dx}2/5 200 [fR#177; {xf"(x)}^2 dx1^2/5

n-2/5.

En conclusion, nous evaluons le MISE en fonction de cette valeur hopt:

M I S E(hopt) = #177; (_20r)

1 2/5 {fly

[fR#177; {xf"(x)}2 dx]

x-1/2f (x)dx ₁2/5

2/5 _n-2/5_.

e. Remar_ques:

i. ????? ?? s?_??rt ?? ?\u9313‡A?? ?ss??e ?x,h ?? ?e_???? _??s ?? ?? x ?? ?? h ??rs ?e?

?\u9312‡@??_???s _q?? ??s ???s tr??té?

ii. ???s ???\u9312‡@_?r?ss?? ?? ?? _???êtr? _?t?????_? ?? ???s?it ?????? f ?t s? ?ér??é? s?????_???r??t ???s ?? ???er?t??r ?t ?? ?e???er?t??r ??tr??r????t ?? ??a _\u9313‡A?éet?_i?? o f s? tr??? s???????t ?? ?e???er?t??r ?? ??s ????s _???i? ???nne ??????? ?nt? ? ?a s_\u9313‡A?etr?_q?? ?t ?s_\u9313‡A?etr?_q??_? ??rs _??r ????ttr? ? ?ée??? ?"??????? ???? ?ée??????st???t?? ?? _??r??etr? h_? f ??t s_\u9313‡Aste??t?_q?????t s???r? ??? ?? ??t???? ?a_\u9313‡A?é? tr?_q?? ?? s?_??rt R? P?r ?\u9312‡@?????? ???s ?? ??s ??s ?\u9313‡A??\u9312‡@ ?ss??és ?????? _???ss???????rs? ?t _???ss??? ????rs? re??_?r_q??_? ??s ?_??s?s ?? f s??t ??? ?? ?s_\u9313‡A?etr?_q???e_??? s?r R+? ???s ?? ??s ??s ?\u9313‡A??\u9312‡@ ?ss??es ?êt?_? ?? ???s?it ??i ???nne ? ?? ?_??or [0,1]?