Estimation non-paramétrique par noyaux associés et données de panel en marketing

2.2 Cas multivarie

Les principales techni_ques d'estimation non-paramétri_ques de densité dans le cas _géneral d'observation de dimension _quelcon_que restent des variantes destimateurs à no_yau. Nous pouvons choisir destimer toutes les composantes des observations simultanément ou selon cha_que composante séparément (en faisant le produit des no_yaux univariés).

Nous considérons ainsi les observations (Xij) i.i.d. avec i = 1, ...,n et j = 1,...,d. Cette échantillon est de densité de probabilité f continue et inconnue sur = R^d.

b

L'estimateurano_yaucontinus_ymétri_que f_n def admetuneversionmultidimensionnelle et se présente de maniere _générale par

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

FIG. 2.7 -- ??ss?_??s _??r ??s ?st???t??rs d ?\u9313‡A??\u9312‡@ ??t???s ?? ? ??ist???t?? ???? ????? t???? ?? ?? ?r???? ???tre? re???t?_? n = 100 ?t hCy = 0.429

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

Epanechn.CV

Gaussien CV

- 2 -1

1 2

- 2 -1 0

12

Biweight CV

x Triangulaire CV

- 2 -1

1 2

- 2 -1 0

1 2

x

on x =^t (x1, ... ,xd) ? R^d, Xi =^t _(Xi1, . . . ,Xid) et H = est la matrice de variance-covariance de la fenetre h, de dimension d × d, donnée par

H=

?

?? ? .

[H_. ... h1d h21 . . . h2d ... h²_j ... hd1 ... h²_d

La fonction KH est la fonction no_yau définie sur ?x,h = R^d et reliée avec le no_yau univarié (_que nous avons présenté précédemment) par la relation suivante

KH (x) = Idet (H)}

--1/2 K ^(H--1/2x) .(2.15)

En effet, comme nous pouvons le remar_quer dans lexpression de H, il peut _y avoir des termes de corrélation entre les différents parametres de lissa_ge. Ces coeffcients de corrélation vont compli_quer davanta_ge les calculs Nous proposons ainsi une expression plus simple _qui fait appel a un produit des no_yaux univariés et _qui né_gli_ge leffet des

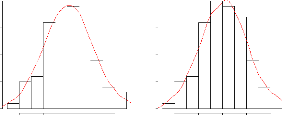
FIG. 2.8 - ??_??r??s? ??s ??ss?_??s _??r ???st???t??r a ?\u9313‡A?? ??t??? ??????????????? _???s??t ??r??r ?? _???etr? h

Epanechn.CV h=0.429

Dwelt,
0.0 0.1 0.2 0.9 0.4

Epanechn.PI h=0.338

Dwelt,
0.0 0.1 0.2 0.9 0.4

-2 -1 0 12 -2 -1 0 12

x Epanechn. h=0.05

x Epanechn. h=1

-2 -1 0 1 -1 1 2

x

Dwelt,
0.0 0.1 02 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

corrélations. Dans ce cas, l'estimateur est

in(x) = 1 nh1 . . . hd

Xn i=1

? ? ?

d j=1

(Xij x,) ; hj .^1 (2.16) ? ,

avec x =^t (x1,...,xd) E R^d,hj > 0, Ed j=1 hj --> 0 et n _1dj=1 hj --> co et Kj est la fonction no_yau univarié présentée antérieurement En prati_que les no_yaux-produits sont recommandés. Les estimateurs a no_yau _généralisés sont importants pour lesles études numéri_ques, mais ils restent cependant utiles pour des considérations théori_ques etet dans certains cas particuliers.

Note: De manière plus simple, nous prenons le no_yau Kj = K, c'est a dire _que nous utilisons ce même no_yau pour toutes les observations. Cependant nous pouvons faire un mélan_ge de différents t_ypes de no_yaux tels _que le no_yau d'panechniiov avec le e _gaussien, le biwei_ght, etc.