Estimation non-paramétrique par noyaux associés et données de panel en marketing

2.1.8 Simulation des donnees

Danscettepartie,nousillustronscertainsestimateursano_yauxcontinuss_ymétri_ques a savoir le no_yau d'Epanechnikov, le no_yau _gaussien le no_yau biwei_ght et le no_yau trian_gulaire. Nous simulons un échantillon de taille n = 100 de la loi normale centrée et réduite. Pour cha_que no_yau fixé, la fenêtre optimale est choisie par les méthodes de validation croisée par moindre carrés et de Plu_g-in

?? ???\u9312‡@ ?? ???etr? _??r P??_????

Cette méthode suppose _que la densité suit une loi normale dans lexpression de la fenêtre h optimale. La valeur du paramètre de lissa_ge est la même pour un échantillon donné. Nous obtenons prati_quement des estimations similairespourcha_queno_yau continu utilisé_; ceci s'expli_que par le fait _que les no_yaux continus s_ymétri_quespossèdent tous des efcacités proches l'une de l'autre (Fi_gure 26)

?? ???\u9312‡@ ?? ???etr? _??r ??????t?? ?r?sé? _??a ??\u9312‡@???? ?? ?v??i????????

Le choix de la fenêtre optimale hopt se fait en fixant au préalable le no_yau continu Le no_yau par défaut dans le lo_giciel R est le no_yau _gaussien. Le choix des no_yaux continus s_ymétri_ques n'est pas important car ils ont _quasiment les mêmes propriétés, c'est pour_quoi le choix de la fenêtre optimale se fait sous lh_ypothèse _gaussienne (et(et aussi pour des raisons techni_ques imposées sous R) Pour cha_que no_yau continu s_ymétri_que fixé, la fi_gure (2.7) présente la fenêtre optimale hCV = 0.1636. Pour cette valeur de h, les estimations des différentes densités sont prati_quement similaires.

?? ???ts ?? ???\u9312‡@ ?? ???êtr?s

Nous comparons différentes estimations en faisant varier la valeur de la fenêtre pour le même no_yau continu. Nous choisissons le no_yau optimal dEpanechniiov

Les simulations effectuées dans la fi_gure (28) mettent en lumière _que les performances prati_ques des estimateurs a no_yaux continus s_ymétri_ques considérés dépendent fortement du choix de la fenêtre h. Par consé_quent, ce choix est plus crucial _que le choix

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

Dwelt,
0.0 0.1 0.2 0.9 0.4

Dwelt,
0.0 0.1 02 0.9 0.4

^bfn(x) = 1 n

Xn i=1

KH (Xi - x) . (2.14)

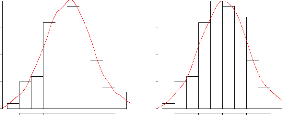
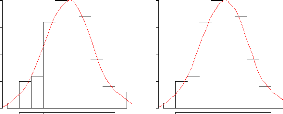
FIG. 2.6 -- ??ss?_??s _??r ??s ?st???t??rs d ?\u9313‡A??\u9312‡@ ??t???s ?? ? ??ist???t?? ???? ????? t???? ?? ?? ?r???? ???tré? r(???t?_? n = 100 ?t hPI = 0.338

Epanechn.PI

Gaussien PI

- 2 -1 0

1 2

- 2 -1

12

x Biweight PI

Triangulaire PI

- 2 -1 0

1 2

- 2 -1

1 2

x

du no_yau. Les valeurs de h sont celles choisies par plu_g-in (h_pi = 0.338), validation croiséeparvraissemblance (hCV = 0.429)etdeuxautresvaleursarbitrairestel_que h = 0.05 et h = 1.