2.1.7 Choix de fenetres
a. Importance du choix de h
Le parametre de lissage h est un réel
positif dont le choix est prépondérant sur celui du
noyau continu symétrique K. Le choix
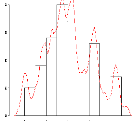
d'une valeur de h trop grande conduit a une courbe trop lisse. La
courbe estimée ne traduit pas suffisament les variations de la vraie
distribution (voir figure 2.3).
FIG. 2.3???str?t?? ???? ??e??e?? ??
s?s???ss??? ?rs ?? ??et???t?? ????? ???n?it
Ep/0/ch0-
-2 -1 0 1 2 3
x
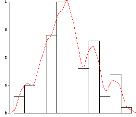
Par contre, en choisissant un parametre de lissage
tres petit que celui adopté précédemment,
l'allure de la distribution change. Il sagit dune
distribution surestimé (figure 2.4).
FIG. 2.4 -- ???str?t?? ???? ??e??e?? ??
s?r???ss??? ?rs ?? ??st???t?? ????? ???n?it
Ep/0/ch0-
D..
-2 -1 0 1 2 3
x
ment la distribution de depart (figure 2.5). Les
courbes obtenues illustrent a quel point
FIG. 2.5 -- Illustration
d'une estimation ideale
Ep/0/00-
RI.
-2 -1 0 1 2 3
x
les formes estimees sont differentes en fonction de lordre
de grandeur du paramètre de lissage. La principale
difculte repose sur le choix optimal de la fenetre h. La valeur ideale hid du
parametre h est celle qui minimise l'erreur
quadratique moyenne integree (MISE).
Pour une taille d'echantillon n donnée et un noyau K fixe,
nous avons
?h
? AMISE(h) = 0.
Ce qui est equivalent a
h3V (K)2 I f" (x)2dx 1 2
jali K(t)2dt = 0.
nh
Ainsi, nous obtenons successivement
nh5V (K)2 ff" (x)2dx
= K(t)2dt R
h5 = nV (K)2 fR
f"(x)2dx
fR K(t)2dt
1 I fR
K(t)2dt11/5
hid = v .
V(K)2 fR f" (x)2dx (2.13)
En particulier pour K = KEpanechn., nous avons
~ 15 \1/5
hid(KEpanechn.) =
n R .
R f"(x)2dx
En definitive, a partir de (2.13), nous obtenons
2/5 4/5 11/5
5 1
AMISE(hid) =
L,Rt2K(t)dt1 {
K(t)2dt1 { f" (x)2dx
4 n4/5 R R
51/5
4n4/5 I(K) fR f"(x)2 dx }
avec
~Z ~2/5 ~Z ~4/5
I(K) = t2K(t)dt K(t)2dt .
R R
Conséquences: Quand n est
grand, hid tend vers 0. Le parametre de lissage h idéal
dépendenfaitdeladensitéatravers f".Ainsipourun
hpetit,nousavonsunpetitbiais et une variance plus grande. Le
noyau optimal est obtenu en minimisant R R K(t)2dt, ceci en
admettant les hypotheses (2.4) et (25).
b. Méthodes de choix de fenêtres
Nous considéronss donce avec plus d'intérêtt
la question de selection du parametree de lissage h.
Comme fenêtree optimale, nous choisissons la valeur qui
minimis lee MISE.
Nous étudions trois méthodes dans la
déterminationn du parametre d lissagee
optimalhopt:: le "Plug-in", la validation
croisée par moindres carrés e laa validation croisée par
maximum de vraisemblance.e
b.1. Mahodee Plng-inn
Dans la procéduree de
Plug-in,l'idée& de base est destimerr dan lexpressionn
(2.13) la quantité inconnue: : fR
f"(x)2dx. En effet, ilt y a deux approches
possibles pou leefaire:: soit nous supposons que la
densité f appartient a une famille de distributions
paramétriques et la nous estimons les
parametres et nous retrouvon facilement cette cette quantité,
soit nous l'estimons par lapprochee non-paramétrique et donce
faire appel a un estimateur a noyau (par exemple). Ceci va
compliquer davantag less calculs parceque nous
trouvons une fonction qui dépendd elle même de h.
Donc,, en gros, la méthode Plug-in résidee
a "injecter" une estimation de f en adoptant une méthode
commode et pratique. Dans notre étude,, nous supposons
que f(x) appartient a une famille de distribution normale centrée
et de variance ó2..
Sous cette hypothese::
ZR R f"(x)2dx =88 0r33
ó-1/550.212ó-1/5..
Il reste alors a remplacer le parametre inconnu óa par la
valeur estiméee bó.. Nous choisissons la valeur
empirique comme valeur optimale définiee comme suit
1
bó
=
n -- 1
Xn
i=1i
tu u v
(Xii -- X~2,,
tel que XX = n-11 (X1 + X2 +
.
· .
· .
· + Xn).
|
=
|
(4ð)-1/10
~
|
1
|
8ð-1/2 bó
~ ~3 ~-1/5
|
|
n1/5 5
|
Le résultatt obtenu sera remplacée dans la formule
de hid et nous avons
hopt
(4bó55~1/5
= 3n ~ bó)= =1.06 6n1/55)
Ce que nous avons accompli en travaillant sous la
supposition de la normalité estest une formule explicite applicable pour
la selection de la fenetre h. En réalité, cette méthode
donne des résultats raisonnables pour toute les distributions
symétriques, unimodales et ne possédant pas
des queues trop lourdes Le probleme donc avec cette méthode
est qu'elle est tres sensible aux valeurs aberrantes. Un estimateur
plus robuste dans ce cas est obtenu a partir de l'intervalle
interquartile : R =
X[0.75n] - X[0.25n] o1 Xp
désignelequantiled'ordrepd'une N
(u,ó2).Ladifférenceentrecesdeuxquartilesdonne
50% de l'ensemble des observations. En supposant toujours
que X suit une normale N(u,ó2), nous posons Z = (X -
u)/ó qui suit une N(0,1). Ainsi, nous montrons que
(X[0.75n] -X[0.250 = 1.34ó Par conséquent, un
estimateur puissant de ó serait Q = R/(1.34). Dans ce cas, le parametre
de lissage optimal est donné par
~ hopt = 1.06 1R.34 n-1/5 0.796n-1/5.
Enfin, la fenetre optimale est
hopt = 1.06 min bó,
1.34
R
n-1/5
.

Cette méthode présente des inconvénients
: si la vraie densité f devie substantiellement
delaformed'unedistributionnormale(enétantmultimodalparexemple)nouspouvons
etre trompés considérablement et nous aurons soit un
sur-lissage soit un sous-lissage.
b.2. Methode de validation croisee par ioindres carrés
Pour un noyau fixé K, le principe de la
validation croisée est la minimisation destimateur de risque
intégré (MISE) par rapport a h. En effet, Le MISE
dépend de la fonction inconnue f et ne peut donc pas etre
calculé. Nous allons essayer de remplacer la MISE par une
fonction de h, mesurable par rapport a l'échantillon et dont la valeur
pour chaque h > 0, est un estimateur sans biais de MISE(h). Pour
cela, notons que :
MISE(h) = E f {:fn(x) - f (x)}2 dx
= E f
R Tfii(x)2dx - 2E 1
fn(x) f (x)dx + IR f2 (x)dx
Le dernier terme ne dépend pas de h, pour minimiser
MISE(h) il suffit de minimiser l'expression :
J(h) = E f fn(x)2dx - 2E 1
fn(x) f (x)dx.
Pour cela, nous déterminons un estimateur des deux
termes de J(h). Le premier terme
JR
fn(x)2dx comme estimateur trivial (d'apres
la propriété des esti-
b
admet l'estimateur
mateurs sans biais : E(bâ) = â).
Il reste a trouver un estimateur sans biais du second terme. Pour
cela, nous admettons par construction l'estimateur sans biais G défini
en tout points du support sauf en Xi :
|
Gb =1
n
|
Xn
i=1
|
bfn,-i(Xi),
|
|
avec
|
bfn,-i(x) = 1
n - 1
|
1 X h
i6=j
|
(x - Xi ~
K .
h
|
Montrons que E( bG) = E{fR
bfn(x)f(x)dx}. Comme les Xi sont i.i.d., d'une part
nous avons
~Z ~ Z ~
Xn ~x - Xi
1
E bfn(x)f(x)dx = E K f(x)dx
nh h
R R
i=1
Z ~x - X1 ~
1 hE K f(x)dx
h
R
Z Z ~x - x1 ~
1 f(x) K f(x1)dx1dx.
h h
R R
D'autre part, nous avons
E(
= E {n1
i=1
= E{In,-1(X1)}
|
= E
|
? ?
?
|
~Xj - X1 ~?
1 X ?
K
(n - 1)h h ?
j6=1
|
~ 1 ~X - X1 ~~ = E hK h
Z Z ~x - x1 ~
1 f(x) K f(x1)dx1dx
h h
R R
Z
= E bfn(x)f(x)dx.
R
Donc, Gb est un estimateur sans biais de fR
biais de J(h) est donne par
b
fn(x)f(x)dx. Finalement, l'estimateur sans
CV (h) = fn(x)2 dx - 2 E bfn,-i(Xi).
n
Ri=1
Et la fenetre optimale est telle que
|
hCV = arg min
h>0
|
CV (h).
|
???? ?et??? ?? ??????t?? ?r?sé? ??r
??\u9312‡@???? ?? ?r??s????????
|
et l'estimateur a noyau
|
fn s'écrit:
|
D(f , jn) = fRf(x) log {
j.f.:(xx))
dx
= IR f (x) log f (x)dx - IR f (x)log {
rn(x)} dx
= E [log { f (X)}] - E [log {fn(X) }1 .
b
|
L'idée de la validation croisée par vraisemblance
est de minimiser D(f,
|
fn). Toutefois,
|
cette distance n'est pas métrique et les
critères définis en la minimisant ne sont pas ap-
b
propriés pour obtenir un lissage
adéquat. Donc minimiser D(f, fn) revient
a maximiser
E [log {fn(X)}1. Ainsi, la fenetre optimale est
LCV (h),
hLCV = arg max
h>0
oU
.
LCV (h) = E [log {fn(X)}]
Par construction, nous avons l'estimateur sans biais de LCV
(h):
|
1
Jn = n
|
Xn
i=1
|
n o
log bfn,-i(Xi|h) ,
|
oU
1
bfn,-i(Xi|h) = (
~Xi - Xj ~
X
K
n - 1)h h
i6=j
n
Montrons que E(Jn) = E h oi.
log bfn(X)
Comme les variables aléatoires X1,X2, . . . ,Xn
sont i.i.d., d'une part nous obtenons
" o#
Xn n
1
E(Jn) = E log bfn,-i(Xi|h)
n
i=1
h n oi
= E log bfn,-1(X1|h)
|
?
= E ?log
|
?
?
?
|
?
~X1 - Xj ~? ?
1 X K ?
(n - 1)h h ?
j6=1
|
= E [log { h 1 K X 1 h X2
D'autre part, nous trouvons
" ( ~)#
h n oi Xn ~X - Xi
1
E log bfn(X) = E log K
nh h
i=1
= E [log { h1 K (X - hX )11
= E(Jn).
Enfin, la fenêtre optimale obtenue par la méthode de
validation croisée par vraisemblance se calcule a partir de :
" 1 n
hLCV = arg max log { fn,_i (Xi | h) }1.
h>0 n
i=1
Cependant, cet estimateur est très sensible aux valeurs
aberrantes. Sa diiculté apparait lorsque la méthode
est appliquée a des observations dont la distribution
présente de grandes queues. Les points
situés dans les queues de la distribution a estimer ont des
valeurs faibles, ce qui implique de faibles valeurs des
estimations correspondantes. La présence de l'opérateur log dans
l'expression de l'estimateur pose un problème de convergence
pour les valeurs de densités aux queues. Par
conséquent, il estest diicile dans ce cas de choisir hLCV de
facon optimale, puisque l'on risque soit le
sur-lissage soit une trop grande erreur sur les
queues.
| 


