Estimation non-paramétrique par noyaux associés et données de panel en marketing

2.1.1 Propriétés élémentaires

Danscettepartie,nousprésentonslespropriétésfondamentalesdelestimateuretles critères d'erreurs usuels. Nous calculons dabord le biais et la variance de lestimateur

b

f_n(x). Ensuite, nous exprimons le ris_que _quadrati_que exact en un point x fixé, puis le ris_que inté_gré. Enfin, nous approximons ces résultats. Dans ce _qui suit, nous supposons _que les dérivées première et seconde de f existent et admettent une inté_grale finie sur le support de la densité ?.

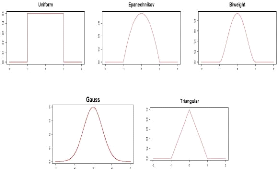
FIG. 2.1 - Illustration des no_yauc continus s_ymétri_ques

b

Propriété 1: La fonction x -?	de prohahilité fn(x) est une densité b
Démonstration: La somme continue de		fn(x) sur le support ? = R est

_{Z Z} (x - Xi )

Xn 1

^bf_n(x)dx = nh K dx

h

R R i=1

_Z (x - X1 ~

1

= _hK dx,

h

R

en posant t = (x - X1)/h et donc dx = hdt, nous trouvons

_{Z Z}

^bf_n(x)dx = K(t)dt = 1.

R R

Deplus,leno_yauK estdéfinipositif.Lasommesurtoutléchantillonresteaussipositive. Par consé_quent, l'h_ypothèse de positivité est vérifiée.

2.1.2 Biais ponctuel

Le hiais ponctuel mesure la différence entre la valeur mo_yenne de lestimateur ^bf_n et la valeur de la fonction inconnue f en un point x.

{ } { }

Biais ^bf_n(x) = E ^bf_n(x)- f(x). (2.6)

Propriété 2: Soit x fixé dans R.

Le hiais de l'estimateur a no_yau présenté dans (21) est

{ } Z

Biais ^bf_n(x) ÿ=¹ ₂h²f⁰⁰ (x) t²K (t) dt. (2.7)

R

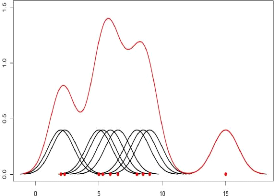
FIG. 2.2 Estimation totale a no_yau _gaussien

Le si_gne » ÿ=» indi_que _que la _quantité à _gauche est é_quivalente à la _quantité à droite. Démonstration: Comme les variables aléatoires X1,X2,.. . ,X_n sont i.i.d., nous avons successivement

( )}

{ } _Xn (x - Xi

1 1

E ^bf_n(x) = E h K

n h

i=1

1
n

_Xn
i=1

{ 1 (x - Xi )} E h K h

{ 1 (x - X1 )}

= E hK h

_Z ~x - x1 )

1

= _hK f (x1) dx1.

h

R

Nous effectuons le chan_gement de variables suivant -t = (x - x1)/h, d'oñ x1 = ht + x.

b

De là, en utilisant l'h_ypothèse (2.2), le biais de f_n(x) s'exprime ainsi par

{ } _Z

Biais ^bf_n(x) = K (-t) f (x + ht) dt - f(x)

Z R

= K (t) f (x + ht) dt - f(x).

R

Dans le but d'avoir une forme plus simple _qui ne dépend _que du paramètre h, nous approximons la formule du biais en utilisant la formule de Ta_ylorrLa_gran_ge

f (x + ht) = f(x) + htf^' (x) + h2t2

2 f'' (x) + o (h2t2).

Ainsi, nous obtenons

Biais { :fn(x) } = f (x) J K (t)dt + hf(x) JtK(t)dt

R R

+2h² f" (x) I t²K(t)dt - f (x) + o(h²).

D'apres les h_ypotheses (2.3) , (2.4) et (2.5) nous avons finalement

Biais { in(x)} 12 _h2 _f00

(x) J_Rt²K (t) dt.

2.1.3 Variance ponctuelle

Propriete 3 : Soit x fixe dans R. La variance de l'estimateur ^bf_n est

Var { :f_n(x)} =ÿ _nhf (x) I K (t)² dt. (2.8)

Demonstration: Partant de l'h_ypothese d'independance entre les Xi, nous avons

-- Xi V ar { :fii(x) } = V ar n {1 ÷`i x K h

i=1

n

1 V ar{ h 11 K (x - _hX1)1

2

E [11 K (x h X1)J ⁾¹² n Lt1 1 [_El_h 1 K (x h X1)j)11

n

1

1 1

n h2 K2 x _h x1) f (x1) dx1

n JR 1 h 1 i1K(x x1)

2 f (x1) dx1 l .

Nous effectuons le chan_gement de variable -t = (x - x1)/h. Nous trouvons

nh²

1 1

V ar { :fii(x) } = K (-t)2 n f (ht + x)hdt - {I_RK (-t) f (ht + x) hdt} 2

h 1 1

I_RK (t)² f (ht + x) dt - n[Biais { :fi_i(x)} + f (x)i²

n

h 1 I_RK (t)² f (ht + x)dt - 1 {O (h²) + f (x)}²

n

Finalement, sous la condition d'avoir f K(t)²dt < +8 et pour n _grand, nous avons

Var { r_n(x)} =ÿ _nhf (x) I K (t)² dt.

2.1.4 Erreur _quadrati_que mo_yenne (MSE)

Propriete 4: L'erreur _quadrati_que mo_yenne (en an_glais "Mean s_quared Error") en un point x fixe s'exprime par

MSE (x) = V ar { :fii(x) } + Biais² {:fii(x) } (2.9)

Demonstration: Nous obtenons par succession

MSE (x) = E [{ 1_n(x) - f (x)}²1

= E ([i_n(x) E { i_n(x)} E { i_n(x)} f(x)i²)

= E ([ 1_n(x) - E { Mx) }i2) + 2E [ 1_n(x) - E { 1n(x)}i

_[E { i_n(x)} f(x)i _[E { i_n(x)} f(x)i 2

= V ar { rn(x) } + Biais² {r_n(x)}

= MSE(x;n,h,K,f).

D'apres les resultats (2.7) et (2.8), l'approximation du critere MSE en un point x fixe est

2

AMSE (x) = _n¹_hf (x) I K (t)² dt + {1 2 h2 f^" (x) I t²K (t)dt } . (2.10)

2.1.5 Erreur _quadrati_que mo_yenne inte_gree (MISE)

Propriete 5: L'erreur _quadrati_que mo_yenne inte_gree (en an_glais "Mean Inte_grated S_quared Error ") est la mesure theori_que commune la plus utilisée pour evaluer lerreur entre la fonction f et ^bf_n. Nous avons etudie dans la partie precedente le comportement de ^bf_n(x) en un point fixe. Il est e_galement convenable devaluer lerreur _globale sur le support R de cet estimateur.

MISE(n,h,K,f) = I MSE(x)dx (2.11)

R

=

IV ar { :f_n(x)} dx + I Biais² {:f_n(x)} dx.

R R

En utilisant l'expression approchee du critere MSE (210) nous avons successivement

AMISE(n,h,K,f) =

h1 JRK(t)^2dt I f(x)dx nh

2

+h⁴ t²K(t)dt } f f"(x)²dx

4 _R

1 J K(t)²dt + ₄¹h⁴ t2K(t)dt }² I

h f^" (x)²dx

nR

avec

V (K) = f t²K(t)dt = V ar(K).

2.1.6 Choix du no_yau

Le premier choix porte sur la nature de la densité no_yau _que nous utilisons. Pour mesurer l'efcacité de chacun des no_yaux continus s_ymétri_ques présenté dans lele tableau 2.1, nous utilisons une mesure commune _qui consiste a calculer le rapport du critere AMISE des deux no_yaux mis en évidence

eff(K1,K2) = AMISE(K1)

AMISE(K2)

Nous supposons _que K1 est le no_yau d'Epanechnikov. Ce no_yau est considéré comme une référence par rapport a tous les autres no_yaux continus classi_ques. Il estest lar_gee ment apprécié pour ses performances (au sens on sa forme répond bien a la plupart des _questions soulevées par le probleme de lestimation non paramétri_que de densité) et il est considéré comme optimal au sens des mesures derreur IlII o~re la valeur défcacité maximale. Nous nous sommes appuis sur les travaux de Ts_ybakov (2004).(2004). Ainsi, apres avoir fait les calculs nécessaires lefcacité dun no_yau K para rapport au no_yau d'Epanechnikov se mesure par

1

VfR t²K(t)dt f_R K(t)²dt < 1.

5V5

eff (K) = 3

Le choix de K dépend seulement de la nature de f et nous admettons _qu'en prati_que le choix du no_yau d'Epanechnikov est le plus staisfaisant Nous donnons lele tableau récapitulatif (Tab. 2.2) _qui présente la valeur defcacité des différents no_yaux continus s_ymétri_ques.

TAB. 2.2 -- E_fficacite des no_yaux continus s_ymetri_ques

No_yau Efficacité

Epanechnikov 1.000

Biwei_ght 0.994

Trian_gular 0.986

Normal 0.951

Uniform 0.930

Commentaire: Danslecasdesno_yauxcontinuss_ymétri_ques,nousremar_quons_que les valeurs d'efcacité des no_yaux tels _que le no_yau biwei_ght trian_gulaire ou Epanechnikov sont tres proches. Par consé_quent Le choix du no_yau nest pas tres important.