Estimation non-paramétrique par noyaux associés et données de panel en marketing

Chapitre 4

Noyau associé discret

Le nombre de travaux abordant les estimateurs a no_yau pour des données discrètes reste limité. Dans ce chapitre, nous présentons deux t_ypes de no_yaux associés discrets. La première section porte sur les no_yaux associés discrets pour des données caté_gorielles on les données sont _qualitatives ordonnées et définis sur un ensemble fini inclu dans N _que nous dési_gnons Rx,h. Ensuite, dans une deuxième partie, nous introduisons le no_yau associé discret pour des données de compta_ges. Une première tentative dans ce cadre, uni_quement de manière expérimentale a été proposé par Marsh & Mukho padh_ya_y(1999).Nousétudionslespropriétesponctuelleset_globalesdechacundesdeux estimateurs a no_yau associé discret Différentes techni_ques de selection de la en:tre du lissa_ge sont proposées. Enfin,nous _généralisonslestimateur a no_yau associé aucasmultivarié.

Definition 1: ??t x ?\u9312‡@( ???s R ?t h > 0? \u9670·?s ?_?????s ??\u9313‡A?? ?ss??e ??s?r?t? Kx,h? t?t? _???t?? ?? ??ss? ?? _?r??????té ??s?rt? ????? ??r????? ??l?t?i? Kx,h s?r ?? s?_??rt Rx,h? t??s _q???

Rx,h n R=6 Ø (4.1)

?xRx,h ? R (4.2)

E(K_x,h) ~ x _quand h ? 0 (4.3)

V ar(K_x,h) < 8 (4.4)

V ar(K_x,h) ? 0 _quand h ? 0. (4.5)

Commentaire: Nous vérifions dans ce _qui suit, _que dans le cas du no_yau associé discret pour des données caté_gorielles, le support Rx,h coincide avec R. Nous verrons _que dans certaine situation, ce n'est pas tou_jours vérifié comme dans le cas des données de compta_ge_; Rx,h dépend de x et ne se colle pas avec le support R.

Definition 2:: ??t X1,. . . ,X_n ?? (????t???? ?? ??r?????s ??e?t?r?s ?????? ?? _???t???? ??ss? ?? _?r??????te f ??s?ret? ??????? s?r R? ???st???t??r a ?\u9313‡A?? ?ss??e ??i?r?t

b

f_n =fn,h,K ?? f ?st ?e_??? _??r

avec x ? ? et h > 0.

Propriété 1: Soit x fixé dans ?. Nous avons

E {:I_n(x)} = E {f(Kx,h)} . (4.7)

Démonstration: En effet, nous trouvons successivement

(

1 n

E {^In(x) } = E n EKx,h(Xi)

i=1

= E {Kx,h(X1)}

X= y??x,h	Kx,h(y)f(y)
X= y??x,h	f(y) Pr(Kx,h = y)
= E{f(Kx,h)} . ·
Propriété 2: Soit f une fonction discrete de support ?. Soit		b fn l'estimateur de f à

no_yau associé discret K_x,h sur ?x,h. Nous supposons _que ?x ? ?,?x,h ? ?. Alors, nous avons

E{in(x)} = E

f(t)Kx,h(t) ? f(x) quand n ? +8.

t??n?x,h

Démonstration:Nouspartonsdel'espérancede _{bfn(x)quiestégaleaEt??n?x,h} f(t)Kx,h(t). Nous calculons sa différence avec f(x). Pour cela, ? ä > 0 tel _que

trn(x)} f(x) =	~~~~~~	X t??n?x,h		{f(t) - f(x)} Kx,h(t)	~~~~~~
X = |t-x|<ä			|f(t) - f (x)| Kx,h(t) + E |t-x|>ä			|f(t) - f(x)| Kx,h(t).

Pourcalculerlepremierterme,nousavonsrecoursaladéfinitiondelacontinuitédansle cas discret (cette notion de continuité est différente par rapport a celle du cas continu) f estcontinueen x ? ? € > 0, ? ä > 0tel_que? t ?]x-ä,x+ä[n?_x,h |f(t)-f(x)| < E. Ce _qui impli_que

X |t-x|<ä

|f(t) - f(x)|Kx,h(t) = E.

La fonction f est discrete donc elle est bornée par 1 et nous obtenons successivement

X |t-x|>ä

|f(t) - f(x)|Kx,h(t) = ä2^2 Pr (|Kx,h - x| > ä)

2 2

ä2V ar _(Kx,h) + ä2 {E _(Kx,h ) - x}² .

Finalement,souslesdeuxconditions(43)et(4.5)toutecette_quantitéconver_gevers 0.

b

Propriété 3: Soit x fixé dans ?. Le biais ponctuel de l'estimateur f_n de f a no_yau associé discret est

Biais {1_n(x) } = E {f(Kx,h)} - f(x)

= f {E(Kx,h)} - f(x) + ¹ V ar _(Kx,h) f ⁽²⁾ (x) + o(h). (4.8)

Démonstration: Par définition,le biais est la différence entrelespérance delestimateur

b

f_n et la densité inconnue f. En effet, d'apres le résultat (4.7) nous avons

E{f_n(x) } = E {f(Kx,h)} .
Or,enutilisantundeveleppomentlimitéaupointmo_yen mx,h = E(K_x,h),nousobtenons

f(Kx,h) = f(mx,h) + (Kx,h - m_x,h)f⁽¹⁾(x) + ¹₂(Kx,h - m_x,h)²f⁽²⁾(x) + o(h). Et en prenant l'espérance mathémati_que, nous avons finalement

1

E{f (Kx,h)} = f {E(Kx,h)} + ₂ V _ar(Kx,h) f ⁽²⁾ (x) + o(h).

Remar_que: Nous mentionnons _que les f^k(x) d'ordre k = 1 représentent les différences finies _qui viennent remplacer les dérivées dans le cas continu et _qui vérifient

f^(k)(x) = { f^(k-1)(x)}

et f⁰(x) =

{f(x + 1) - f(x - 1)} /2 si x ? N^* f(1) - f(0) si x = 0.

? ???

???

Propriété 4:: Soit x fixé dans ?. La variance ponctuelle de l'estimateur ^bf_n =fn,h,K de f a no_yau associé discret est

V ar {^In(x) } =ÿ¹ _nf(x)Pr(Kx,h = x).

(4.9)

Démonstration: La variance est donnée de maniere successive par

( n

V ar {:fi_i(x) } = V ar K x,h(Xi)}

n i=1

V ar {Kx,h(X1)}

1

E {Kx,h(X1)}² - n [E {Kx,h(X1)}]²

1

=

n

1
n

=

}2

1
n

? ? ?

=

f (y) {Pr(Kx,h = y)}² - 1 _n?E f (y) Pr(Kx,h = y)

yENx,h ?yENx,h

1
n

=

n1 {f (x) E(K_,h) - f²(x) } + O(_n) f(x) Pr(Kx,h = x).

Nous précisons _que le terme E(K2x,h) := Ey??x,h {Pr(Kx,h = y)}² est ma_joré par 1. Le
résultat final se base sur la condition (4.3) a traversla probabilité modale Pr(Kx,h = x).

Propriété 5: L'erreur _quadrati_que mo_yenne inté_grée _que nous appelons MISE est

X MISE = x?? X= x??

E{in(x) - f(x)}^2 Biais^2 {.^-fii(x)} + E x??

V ar {:fii(x)}

1²

= E {E(Kx,h) - f (x) + ²¹ V ar(K_x,h)f⁽²⁾(x) + o(h)

x??

+ E x??

1 n

f(x)Pr(Kx,h = x). (4.10)

4. 1 Noyau associé discret pour des données catégorielles

Dans cette partie, nous nous focalisons sur les données discretes caté_gorielles (i.e. données _qualitatives). Nous travaillons essentiellement sur un ensemble discret fini ? ? R. Nous si_gnalons _que durant les dernieres annéesil_y avait une croissanceconsidée rable dans le domaine des no_yaux discrets pour des données caté_gorielles, lesles premiers travaux sont dfis aux innovateurs Aitchison & Aitken (1976) puis Simonoff & Tutz (2000) et enfin, Racine & Li (2007). (voir biblio_graphie pour plus de détails.)

Définition 3: Soit X la variable aleatoire de loi d'Aitchison & Aitken _que nous notons D(c; c0,A), on c ? N \ {0,1} est le cardinal du support, c0 ? {0,1,. . . ,c - 1} est le point de re_ference et A ?]0,1], de densite de probabilite sur le support ? = {0,1, . . . ,c - 1} de_finie par

Pr(X = x) = (1 - A)1x=0 + c A - 1

1x6=c0.

Propriété 6: L'espérance de la variable aléatoire X de loi d'Aitchison & Aitken est

A

E(X) = c0(1 - A ^Ac (4.11)

c - 1 2

4.1. NOYAU ASSOCIR DISCRET POUR DES DONNRES CATRGORIELLES 69

Demonstration:L'esperancedecettevariablealeatoireestdonnéedemanieresuccessive par:

E(X) = E x Pr(X = x)

x?{0,1,...,c-1}

+

c xë11x,c0

E { x?{0,1,...,c-1}

= {c0(1 -- ë) + c ë ₁(0+ 1 + ... + (c0 -- 1) + (c0 + 1) +...+c -- 1)1

( ) }

= c0(1 -- ë) +

c ë -- 1 i c0₀

c(c -- 1)

= c0(1 -- ë) + c -- ë 1 1 2 c0}

c0 (1 ë ë ) ëc

c 1 2

Propriete 7: La variance de la variable aleatoire X de loi d'Aitchison & Aitken est

V ar X 2 c²ë (1 -- ë) -- ëc

( ) =

⁰(c -- 1)²

2

ëc (2c 3 -- 1 ë ₂c)

. (4.12)

c0

c -- 1

c²ë(1 -- ë) -- ëc

+

Demonstration: La variance est obtenue de maniere successive par

V ar(X) = E(X²) -- {E(X)}²

(c-1 ) -- co = c²0(1 -- ë) + c ë

Ei² c,0--{c0 (1 -- ë

c ë ₁ )) ëc

2 f

i=0

= c^20(1 -- ë) +

ëc(2c -- 1) ëc8 {c0 (1 -- ë -- ë ) ëc1 c -- 1 ) 2 j 6 c -- 1

2

2

ë

2c2

ë

= c0 ² (1 -- ë

c 1

ë ) 6 Ac(2c -- 1) 2

c0 (1 -- ë

c -- 1 ) 4

--c0ëc (1 -- ë -- ë )

c -- 1

(c -- 1)²

c0

c -- 1

2 c²ë(1 -- ë) -- ëc = c0

Commentaires::

c²ë(1 -- ë) -- ëc

+

ëc (2c -- 1 ëc)

.
·

2 3 2

a. Lors_que c = 2, nous nous retrouvons dans le cas dune loi Bernoulli de parametre ë ou 1 -- ë. Le t_ype de la loi Bernoulli chan_ge selon _que le point de reference se trouve en 0 ou en 1. Nous verrons dans le cas de lestimateur a no_yau associe discret _que le choix du point de reference sera la cible.

b. Lors_que c 7? +8, le support ? = N.

c. Si ë = 0, ceci revient a dire _que notre loi est la loi de dirac _qui ne depend plus

FIG. 4.1 -- ???str?t?? ?? ?? ?? ????t???s? ?t ??t???

Densité de loi Aitchison et Aitken

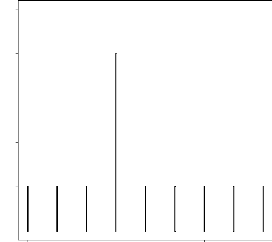
OA 02 0.4 0.8 0.8 1.0

Pr

0 8

4

2

x

de c et _que nous la notons ä_x. Si maintenant, ë prend la deuxieme valeur limite _qui est e_gale a 1 alors Pr(X = x) = ¹ 1

c-1 x,c0.

Nous sommes en mesure de donner une definition precise dun estimateur a no_yau associe discret pour une densite de probabilite f sur un ensemble discret ? et de presenter les proprietes fondamentales relatives

Definition 4: ??t X1,X2,. . . ,X_n ?? e????t???? ?? ??r?????s ??e?t?r?s ?????? ?? ???

t??????ss???_?r??????te??s?ret???té_?r?????r???é??????? f s?r? = {0,1,...,c - 1}_?

ùc ?st ???? ?t _?\u9312‡@e ???s N \ {0,1}? U? ?st???t??r ^bf_n(x) =

b

fn,h,K(x) ?? f(x) a ?\u9313‡A?? ?ss??e ??s?r?t _{KD(c;x,h) q}?? s??t ?? ?? ????t???s? & ??t??? ?st ?e_??? _??r

fn(x) = 1 n	Xn i=1	KD(c;x,h)(Xi) (4.13)
1 n	E- h)1Xi=x + h 1^1Xi,=x} . i=1

???? x ?st ???s ? ?t h ?]0,1] ?st ?? _??r??etr? ?? ??ss?_?? ??s?r?t ?? ???r? ?? _???êtt??? Nous examinons les differents points _que doit verifier le no_yau associi KD(c;x,h):

i.?c;x,h = {0,1, . . . ,c - 1} = ?.

4.1. NOYAU ASSOCIE DISCRET POUR DES DONNEES CATEGORIELLES 71

FIG. 4.2 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e ???t???s? ?tet ??i??? _??r h = 0.2 ?t x ??r?e

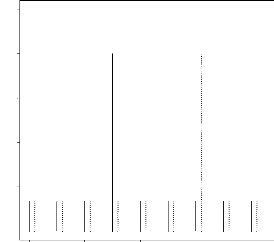
0.0 02 0.4 0.6 0.8 1.0

D(c;x,h)(y)

0 2 4 6 8

y

ii.?x?c;x,h = {0,1,...,c 1} = ?.

iii. E (KD(c;x,h)) = x (1 h ch 1) + ^hc~ x _quand h ? 0.

iv. V ar (KD(c;x,h)) = _x2 hc²₍(1-h)₂-hc _xhc² (1-h)-hc + hc (2c-1 h2c) < 8.

c-1 2 k 3

v. h ? 0 V ar (KD(c;x,h)) = 0.

Propriété 8: A travers la formule (4.8), la fonction x 7? ^bf_n(x) est une fonction de masse de probabilité.

Démonstration: Comme les Xi sont i.i.d., nous avons successivement

Ec- 1 x=0

fn(x) =

c- 1 {1 n =0 n D(qx,h)(Xi) x } i=1

c- 1

E {(1 h)1X1=x + h

c 11X1'=x

x=⁰

= (1 h) + ch ₁(1 + 1 + ... + 1)

= (1 h) + ch ₁(c 1) = 1.

FIG. 4.3 -- ???str?t?? ?? ?\u9313‡A?? ?ss??e ???t???s? ?tet ??i??? _??r x = y = 2 ?t h ??r?e

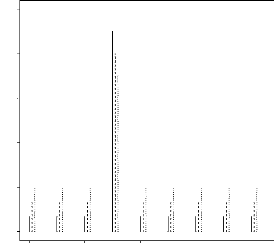
0.0 02 0.4 0.6 0.8 1.0

D(c;x,h)(y)

0 2 4 6 8

y

b

Propriété 9: D'après la relation (4.8), le biais de l'estimateur	fn de f a noyau associé

{ I

²hc

(

2c 1

+
hc

)}

Biais{fn()} x) = hc f⁽¹⁾(x) + - xhc + f ⁽²⁾ ( 2)

x) + o(h.

2 2 lc - 1 2 3 2

(4.14) Remar_que: \u9670·?s r???r_q??s ???_?res ?????? _q?? ?? ????s ?stest rs ??_?rr??t? ? ?d????? a ?? _??s ?? c_? h ?t ??s ?er??e?s _?r???er? ?t s?????? ???_q?? _??s _q?? ? ??r??????? s?_??rt c ??_????t? ?? ????s s????r?t? \u9670·?s ????s ???s? _???s?r a r???i? ? ????i ?? ???_???t ??s _??r??etr?s ???? ???s ??le ??s ??s ?\u9313‡A??\u9312‡@ ?ss??ie ?a_\u9313‡A?éet?_i??e ?_???u _?re??se????t ??s ?\u9313‡A??\u9312‡@ ????? ?t ?et? ?? ????? _???ss??? ???er? ?e _???us??? ???er? re??_?r_q?? ?? ???????t? \u9670·?s ??tr?s _q?? ?? ??st _??s ?????t ?? ?de?e????e ?e_??a???etr?s? ??_??????t_? ??? _??_c? _?ss???? _??r ??le é???r? ??s?is? a _?r???d? ??? ? ???ntr??? c0 ???? ? _???t ?? ????? ??sse _??r ??s ?\u9313‡A??\u9312‡@ r???_?????r?e ???i ?????_?g?_????_??r _???s ?? ?et???s??

b

Propriété 10: D'après la relation (4.9), la variance de l'estimateur associé discret KD(c;x,h) de loi d'Aitchison & Aitken est

fn de f a noyau

h _\2 {c-1

V ar {:fi_i(x)} = 1 [f(x)(1 - h)² + (c - ₁) f(i) - f (x) }1. (4.15)

i=0

4.2. NOYAU ASSOCI] DISCRET POUR DES DONNÉES DE COMPTAGE 73