4.3.2 La méthode PLS-Mixte sur un modèle a`
effets aléatoires corrélés de variances
hétérogènes
La méthode PLS-Mixte, présentée ci-dessus
et appliquée aux données de NIRS, a
étéécrite avec les hypothèses classiques de
normalitédes effets aléatoires et surtout de la forme
particulière des matrices de variance de ces effets aléatoires.
En effet, il a fallu supposer que cette variance pour chaque effet
aléatoire Uk était de la forme
ó2 kIqk.
Ici, nous allons légèrement relâcher cette
hypothèse et considérer que la va-
riance pour chaque effet
aléatoire pourrait être de la forme ó2
kAk o`u Ak est
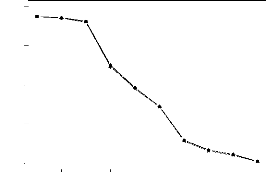
Variation du PRESS selon les dix premières
variables latentes
FIG. 4.4 quand le nombre maximum de variables a
initialement étéfixéde façon successive a` 10, 20,
30, 40 et 50 pour le modèle fondésur
ML pour les données de NIRS. Le modèle
fondésur REML donne des résultats voisins de ceux
présentés ici.
ML
20 25 30 35 40
PRESS
2 4 6 8 10
une matrice quelconque symétrique connue. Nous allons
alors voir comment la méthode PLS-Mixte s'écrira avec ces
nouvelles données du problème.
Nous nous plaçons toujours dans le cadre du modèle
(4.2) que nous allons rappeler.
Y = Xâ + Xr ZkUk
(4.7)
k=0
Nous supposons cette fois-ci donc que Uk ~ N(0,
ó2 kÄk), d'o`u V = Xr
ZkÄkZ' kó2
k.
k=0
Avant de présenter notre méthode avec un
modèle o`u n < p et la variance
V
des observations écrite comme ci-dessus, nous traiterons dans
un premier
temps, du cas plus simple n > p o`u nous
verrons comment s'effectuent les estimations des paramètres inconnus
â et ó2 k a` l'aide de
l'algorithme EM fondésur ML.
Le modèle mixte a` effets aléatoires
corrélés
L'algorithme EM, nous le rappelons, permet de calculer
l'espérance condi-
tionnelle des effets aléatoires sachant les
données incomplètes Y. Pour cela, il
est
nécessaire d'avoir la loi jointe de Y et u = [
u'1 u' 2 ... u' r
]'. Nous avons
Cov(Y, u' k') = Cov(Xâ
+ Xr Zkuk,u' k') =
Zk'Cov(uk',u' k') = ó2
k'Zk'Äk' (4.8)
k=0
car Var(uk) = ó2 kÄk V
k, et Cov(uk,u'k') = 0
pour k =6 k'.
Ainsi, avec les suppositions du modèle
(4.7), la loi jointe de Y et u
est gaussienne de la forme .IV(12,Ó)
o`u
|
12 =
|
Xâ
0
...
0
|
?
? ? ? ? et Ó =
?
|
" #
V Cov(Y,u')
Cov(u,Y') Var(u)
|
(4.9)
|
avec Cov(Y,u') = [
ó2 1Z1Ä1 . . .
ó2 rZrÄr ]
?ó21Ä1Z'1
?
Cov(u,Y') = ? ..
? .
ó2
rÄrZ' r
ó2 1Ä1
et Var(u) = 0 ... 0
ó2 rÄr
Ce qui implique la fonction de densitésuivante
Pr
fY,u1,···
,ur(Y, u1, · · · ,
ur) = (2ð)-
1 k=0 qk|Ó|-
1
o`u
2 2 exp(-1 2Q) (4.10)
|
[ ]
Q = (Y - Xâ)'
u' 1 · · · u'
Ó-1
r
|
Y -
Xâ
u1
...
|
(4.11)
|
ur
Nous allons donc avec les développements qui vont
suivre, trouver les valeurs de |Ó| et de
Ó-1 dans le but de simplifier la
densité(4.10). Il s'agira par la suite, de
dériver tout simplement cette densité, pour avoir les estimations
des paramètres.
Pour calculer |Ó|, nous faisons appel au
résultat déjàétabli (Searle et alp 453, 1992) : Si
A, B, C et D
sont quatre matrices avec les bonnes dimensions, alors
|
~~~~~
|
A B
C D
|
~~~~~
|
= |D||A - BD-1C|
|
|
Ainsi,
|Ó| =
|
~~~~~
|
V Cov(Y,u')
Cov(u,Y') Var(u)
|
~~~~~
|
= |Var(u)||V - Cov(Y,
u')(Var(u))-1Cov(u,
Y')|
|
|
|Var(u)| =
|
~~~~~~~~
|
ó21Ä1
0 ... 0
ó2 rÄr
|
~~~~~~~~
|
=
|ó21Ä1| ×
··· × |ó2
rÄr| =
|
Lr
k=1
|
(ó2
k)qk|Äk|
|
Or,
car chaque matrice Äk est carree de nombre
de lignes qk D'autre part,
Cov(Y,
u')(Var(u))-1Cov(u,
Y')
|
= [
ó21Z1Ä1
··· ó2 rZrÄr ]
|
ó1
2Ä1-1
0
·
·
·
0
ó-2
r Ä
|
-1 r
|
ó2
1Ä1Z'
1
·
·
·
ó2rÄrZ'r
|
|
=
|
Xr
k=1
|
ó2kZkÄkZ'
k
|
Or,
(Var(u))-1Cov(u,
Y') =
0
·
·
·
0
ó-2
r
Ä
ó21Ä1Z'1
·
·
·
ó2rÄrZ'r
-1
r
ó-2
1 Ä1-1
=
Z'1
·
·
·
Z'r
D'o`u
|Ó| = Yr
(ó2k)qk|Äk||V -
Xr ó2
kZkÄkZ' k|
=
Yr
k=1
k=1 k=1
(ó2k)qk|Äk||ó20Ä0|
Pour calculer Ó-1, nous
utilisons les resultats des inverses generalisees (Searle et al p 450, 1992) et
etablissons que
" #
=
0 0
0 (Var(u))-1
"+
# I
ó,:72Ä:7,
1 [ I -Cov(Y,
u')(Var(u))-1
-(Var(u))-1Cov(u,
Y')
Par ailleurs,
Cov(Y,
u')(Var(u))-1 = [
Z1 · · ·Zr
Par cons'equent,
Ó-1 = Ó1
-1 + Ó-1
2
o`u Ó1 1 =
ó-2
1 Ä-1
1
?
m ?0
... 0
ó-2
r Ä-1
r
I
|
et Ó2 -1 =
|
-
|
Z'1
...
|
h h i i
ó-2
0 Ä-1 I - Z1
· · · Zr
0
|
Z' r
Nous allons donc remplacer Ó-1
par Ó-1
1 +Ó-1
2 dans (4.11) pour avoir la valeur
de Q.
Ainsi,
Q = Q1 + Q2
|
o`u Q1 = [ (Y -
Xâ)'
u'1 · · · u'
Ó-1
r 1
|
Y - Xi3
u1
...
|
ur
|
et Q2 = [ (Y -
Xâ)'
u'1 · · ·
u'Ó-1
r 2
|
Y - Xi3
u1
...
ur
|
m 0
m ?0
?
? ó-2
1 Ä-1
1
... 0
r 2Är-1
ó
Q1 = [ (Y -
Xâ)'
uc. · · ·
u'r ]
Y - Xi3
u1
...
ur
= I 0 [ u'1
· · ·
u'r ]
|
ó-2
1 Ä-1
1
0
|
...
0
ór
2Är-1
|
Y - Xi3
u1
...
ur
|
|
= [ u'1 ·
· · u'r
]
|
ó-2
1 Ä-1
1
0
|
...
0
ór
2Är-1
|
u1
...
ur
|
u'kÄk
1uk
=
ó2
k
Er
k=1
Pour calculer Q2, trouvons d'abord une formule
simplifiée de Ó-1
2
I
Ó-1
2 =
|
-
|
Z'1
...
Z'r
|
ó
0 2Ä,Y1 [ I - [
Z1 ··· Zr ] ]
|
|
Ä01
-Ä,y1 [ Z1
·
1
|
·· Zr ]
|
|
= ó-2
0
|
-
|
Z'1
...
Z'r
|
? ?
Ä-1 ?
0 ?
|
Z'1
...
Z'r
|
Ä01 [ Z1 ·
· · Zr ]
|
|
Ainsi Q2 = ó02
[ Q21 Q22 ]
|
Y - Xi3
u1
...
ur
|
|
?
?
avec Q21 = (Y -
Xâ)'Ä-1
0 - [ u' 1 · · ·
u' r ] ? ?
Ä-1
0 [ Z1 · · · Zr
]
Z' r
Z' 1
...
? ?
et Q22 =
-(Y-Xâ)'Ä-1
0 [ Z1 · · ·
Zr ]+[ u' 1 · · · u'
r ] ? ?
D'o`u,
Z'1
...
Z'r
? ?
Q2 = ó-2
? r ]
0 ?(Y -
Xâ)'Ä-1
0 - [ u' 1 · · ·
u'
? ?
? ?
? Ä-1 ? (Y -
Xâ) ? 0 ?
Z'1
...
Z'r
?
? ? ?
- ó-2
0
? ?
(Y -
Xâ)'Ä-1
0 [ Z1 · · ·
Zr ] - [ u' 1 · · · u'
r ] ? ?
?
? ?Ä-1
0 [ Z1 · · · Zr
]
?
u1
- 2 (Y -
Xâ)'Ä-1
0 -
Xr
k=1
!
u' kZ'
kÄ-1 (Y -
Xâ)
ó0
=
0
- ó-2
0
|
(Y -
Xâ)'Ä-1
0
|
Xr
k=1
|
Zkuk -
|
Er
k=1
|
u'kZ'kÄ0-1
|
Xr
k=1
|
!Zkuk
|
|
!
Xr Xr
Zkuk - ó-2
u' kZ'
kÄ-1 Y - Xâ -
Zkuk
0 0
k=1 k=1
- 2 (Y -
Xâ)'Ä-1
Y - Xâ -
0
Er
k=1
ó
=
0
! Xr
u' kZ'
kÄ-1 Y - Xâ -
Zkuk
0
k=1
- 2 (Y -
Xâ)'Ä-1
0 -
Xr
k=1
= ó 0
|
= ó-2 Y -
Xâ -
0
|
Xr
k=1
|
!' Xr
Zkuk Ä-1 Y - Xâ
-
0
k=
|
1
|
Zkuk)
|
u' kÄ-1
k uk + ó-2 Y -
Xâ -
ó2 0
k
) !
X
Zkuk Ä-1 Y - Xâ
- Zkuk (4.12)
0
k=1
Q =
Xr
k=1
Er
k=1
' r
En ajoutant Q1 et Q2, nous
obtenons
En remplaçant (4.11) dans
(4.9) et en passant au logarithme, nous avons
|
l = -1
2
|
X r
k=0
|
log27r --
) k -
k=0 k=1
1 Er (gkiegOlc +
loglAkl) -- 1 `-r uk'
Ä-1u1 qk '
2
2 L--1
ó2
k
|
Zkuk) Ä0 1 Y
- Xâ-
-2 ó0
2
Y - Xâ -
Xr
k=1
EZkuk)
k=
1

1
-
2
X r
k=0
) 1(qklogó
r r 1.1'
Ä-1uk
qk log27r --
Nlc + log|Äk |) - V k k
2 1---/ 2 L--/ ,.,.2
"
k=0 k=0 k
car Y - X0 - Xr Zkuk = e =
u0
k=1
De ce fait, il suffira de d'eriver la fonction l
ci-dessus par rapport a` chacun des param`etres inconnus du mod`ele
(4.7) pour trouver les estimateurs suivants
= ukÄk
1uk/qk, k = 0,1,· · · r (4.13)
et
XS =
X(X'Ä,y1X)-X'Ä,y1
Y -
k=1 Zkuk) ) (4.14)
Ainsi, comme les uk ne sont pas connus, nous
avons besoin des esp'erances conditionnelles de
u'k k
1uk
et de
r
Y - Zkuk
k=1
sachant les donn'ees incompl`etes Y.
Pour cela, nous pouvons utiliser le r'esultat suivant : si
I # I #
I
x1 u1 V11
V12
~ N ,
x2 u2 V21
V22
alors la loi conditionnelle de x1 sachant
x2 est
x1|x2 ~ N[u1
+ V12V-1
22 (x2 - u2),
V11 - V12V-1
22 V21]
Avec uk ~ N(0,ó2
kÄk) et Y ~
N(Xâ,V), nous avons
I # I #
I #!
uk 0 ó2 kÄk Cov(uk,
Y')
~ N ,
Y Xâ
Cov(Y,u' k) V
D'apr`es (4.8), il vient
uk|Y ~ N (ó2 )
kÄkZ'
kV-1(Y - Xâ),
ó2 kÄk - ó2
kÄkZ'
kV-1ó2 kZkÄk
D'o`u
kV-1(Y -
Xâ)
[(uk|Y) = ó2
kÄkZ' (4.15)
Ensuite, en utilisant le th'eor`eme suivant (Searle p 231,
1987)
Théorème 1
si x ~ N(u, V)
alors[(x'Ax) = tr(AV) +
u'Au ? A
et d'apr`es ce qui pr'ec`ede, nous avons
kÄ-1
kÄ-1
E(u' k uk|Y) =
tr(ó2 kÄ-1
k Äk - ó4 k
ÄkZ'
kV-1ZkÄk)
+ó4k(Y -
Xâ)'V-1ZkÄ;cÄk
1ÄkZ'kV-1(Y
- Xâ)
D'o`u
E(u'kÄ-1
k uk|Y) = tr(ó2kIqk -
ó4kZ'kV-1ZkÄk)
+ó4k(Y -
Xâ)'V-1ZkÄ'kZ'kV-1(Y
- Xâ) (4.16)
Nous pouvons alors établir l'algorithme EM dans le cas
du modèle linéaire mixte o`u chaque effet aléatoire est de
variance
ó2kÄk.
L'estimation, fondée sur ML, s'effectue en plusieurs itérations.
Des valeurs initiales ók 2(0) et
â(0) sont choisies au départ. A la
me itération de l''Etape-E, sont calculées
les espérances conditionnelles suivantes, a` partir de
(4.16),
g(k m) =
E(ukÄk
1uk|Y)|0=0(0) et
óZ=óZ(m) (4.17)
=
tr(ók(m)Iqk)
- ó4(m)
k tr(Z'
kV-1(m)ZkÄk)
+ók
4(m) (Y -
Xâ(m))'V-1(m)ZkÄ'kZ'kV-1(m)(Y
- Xâ(m)) =
qkók + (ó4(m)
2(m) k )
× [ (Y -
Xâ(m))'V-1(m)ZkÄ'kZ'kV-1(m)
(Y - Xâ(m)) -
tr(Z'kV-1(m)ZkÄk)]
Et, a` partir de (4.15)
|
b(m)
=E(Y -
|
Xr
k=1
|
Zkuk|Y)0=0(0) et ó2
(4.18)
k=ó2(m)
k
|
= Y - Xr
ZkÄkZ;có2k
(m)V-1(m)(Y
- Xâ(m))
k=1
= Y - (V(m)
-
ó,!,(m)Ä0)V-1(m)(Y
- Xâ(m))
= Y -
V(m)V-1(m)(Y
- Xâ(m)) +
ó02(m)Ä0V-1(m)(Y
- Xâ(m)) =
Xâ(m) +
ó0
2(m)Ä0V-1(m)(Y
- Xâ(m))
A l''Etape-M, pour trouver les estimateurs, il suffit de
prendre
|
ók
2(m+1)
|
.ik m)/qk
(4.19)
|
= 4,(m) +
(4(m)/qk)
× [(Y -
Xâ(m))'V-1(m)ZkÄ;,Z'kV-1(m)(Y
- Xâ(m)) -
tr(Z'kV-1(m)ZkÄk)]
Et, a` partir de (4.14)
Xâ( 1)
=
X(X'Ä,y1X)-X'Ä,y1
(Xâ(m) +
ó0
2(m)Ä0V-1(m)(Y
- Xâ(m)) )
(4.20)
=
X(X'Ä-1
0
X)-X'Ä-1
0
Xâ(m) +
ó0(m)X(X'Ä,y1X)-X'ÄC,1Ä0V-1(m)(Y
- Xâ(m)) =
Xâ(m) +
4(m)X(X'Ä1X)-X'V-1(m)(Y
- Xâ(m))
A la place d'itérer pour obtenir a` la fois les valeurs
de â et de
ó2k, Laird (1982)
suggère de trouver les valeurs de
ó2k et seulement, a` la fin des
itérations, de calculer la valeur de â. En effet, a` la place de
calculer V-1(m)(Y -
Xâ(m)) dans
l'équation (4.19), il est
calculéP(m)Y
o`u
P(m) =
V-1(m) -
V-1(m)X(X'V-1(m)X)-X'V-1(m)
ne depend pas de â.
En effet, si
Xâ(m) etait l'estimation de
Xâ, c'est-`a-dire
Xâ(m) =
X(X'V-1(m)X)-X'V-1(m)Y
alors
V-1(m)(Y
- Xâ(m)) =
V-1(m)Y -
V-1(m)Xâ(m)
= V-1(m)Y -
V-1(m)X(X'V-1(m)X)-X'V-1(m)Y
= (V-1(m) -
V-1(m)X(X'V-1(m)X)-X'V-1(m))
Y
=
P(m)Y
De ce fait, il ne sera pas necessaire de disposer de
â(m) dans les iterations et a`
l''Etape-E.
Il ne sera alors plus calculequ'une seule esperance conditionnelle
|
ó2(m+1)
k =
|
bs(m)
k /qk (4.21)
|
= ó2k
(m) +
(4(m)/qk) [
Y'P(m)ZkÄ'kZ'kP(m)Y
-
tr(Z'kV-1(m)ZkÄk)]
Nous presentons ci-dessous l'algorithme EM fondesur ML
appliqueaux effets aleatoires corr'el'es du mod`ele mixte.
'Etape 0 Mettre m = 0 et
choisir des valeurs initiales
ó2k(0)
'Etape 1 ('Etape-E) Calculer
Q(ó2 |
ó2(m))
= Eó2(m) (ukÄk
1uk | Y)
= qkók (Irk2(m)
+ 4(m)
[Y'P(m)Zk k
Ä' Z'
P(m)Y --
tr(Z'kV-1(m)ZkÄk)1
o`u P(m) =
V-1(m) --
V-1(m)X(X'V-1(m)X~-X'V-1(m)
'Etape 2 ('Etape-M) Determiner
ó2k(m+1) qui maximise
Q(ó2 |
ó2(m)) c'est-`a-dire,
tel que
Q(ó2(m+1) |
ó2(m)) ?.
Q(ó2 |
ó2(m)). Alors,
ók2(m+1)
= E 2(m)
(ukÄi;1uk | Y)/qk
for k = 0,1,
·
·
· , r
'Etape 3 A la convergence c`ad
L(ó2k (m+1) | Y) --
L(ó2k (m) | Y) ,....
ç o`u
ç est une quantitearbitrairement petite
et L la fonction de vraisemblance, prendre
bó2k =
ók2(m+1) et alors calculer
X-â =
X(X'V-1(m+1)X)-X'V-1(m+1)Y
sinon ajouter 1 a` m et
retourner a` l''Etape 1.
Simulations pour la convergence de l'algorithme EM
appliqu'e aux effets al'eatoires corr'el'es du mod`ele mixte :
Pour tester la convergence de cet algorithme et verifier la
qualitedes estima-
tions, nous avons effectuedes simulations numeriques.
Nous avons considerea` cet effet le modele simple suivant :
Y = X/3 +
Z1u1 + Z2u2
+ Z0u0 (4.22)
o`u la dimension du vecteur des reponses Y
est 120x1, celle de la matrice des observations
X est 120x5 et le vecteur 13
des parametres fixes est de longueur 5. Aussi, avons-nous suppose
|
? ????
????
|
u1 ~
N(0,ó21Ä1)
u2 ~ N (0, ó2
2Ä2)
u0 ~ N (0,
ó2 0Ä0)
|
|
?
o`u Ä1 =
???????
|
2 1 1 1 1
|
1 1 1 1 1
|
1
1
2
1
1
|
1
1
1
2
1
|
1 1 1 1 1
|
?
,
???????
|
?
? ? ? ? ? ? ? ? ? ?
Ä2 =
|
3 1 1 1 1 1
|
1
2 1 1 1 1
|
1 1 1 1 1 1
|
1
1
1
3
1
1
|
1 1 1 1
3
1
|
1 1 1 1
1
2
|
?
et Ä0 = I120.
??????????
|
Nous avons choisi un dispositif équilibréavec le
facteur 2 (6 niveaux) hiérarchisédans le facteur 1 (5 niveaux).
Les matrices Z1 et Z2 sont donc les
matrices
d'incidence correspondantes a` ces deux facteurs tandis que la
matrice Z0 est l'identitéd'ordre 120.
Nous présentons au Tableau 4.3 les résultats des
simulations obtenues avec le modèle 4.22 sur 300 jeux de
données.
|
Valeurs simulées
|
Valeurs estimées
|
|
0,5402
0,8948
|
Moyenne
0,5380
0,8974
|
'Ecart-type
0,0937
0,0931
|
|
â
|
0,6476
|
0,6423
|
0,0912
|
|
0,9513
|
0,9526
|
0,0921
|
|
0,0772
|
0,0748
|
0,0933
|
|
ó21
|
0,4653
|
0,4241
|
0,4416
|
|
ó2 2
|
0,2458
|
0,2471
|
0,3324
|
|
ó2 0
|
0,9226
|
0,8874
|
0,1233
|
TAB. 4.3 - Résultats des simulations pour un
modèle mixte a` effets aléatoires corrélés
effectuées sur 300 jeux de données.
Au vu de ces résultats, les valeurs estimées pour
les paramètres ne sont pas, en moyenne, éloignées des
valeurs simulées.
Le modèle PLS-Mixte a` effets aléatoires
corrélés
Nous venons ainsi de voir, a` la section pr'ec'edente,
l'estimation des paramètres
fixes et des composantes de variance dans
un modèle lin'eaire mixte, a` l'aide
de l'algorithme EM, o`u chaque
effet al'eatoire est de variance ó2 kÄk
et o`u n > p.
Le cas n < p avec cette même
structure de variance des effets al'eatoires, n'ecessite, comme au chapitre
pr'ec'edent, d'imbriquer la r'egression PLS, en tant que m'ethode de r'eduction
de dimension, a` l'algorithme EM. Nous proposons l'algorithme PLS-Mixte
suivant, fond'e sur la variation de ML propos'ee par Laird
'Etape 0 Mettre m = 0 et
choisir des valeurs de depart
ó2k(0)
'Etape 1 Centrer et reduire X
et Y : x0 = X,
y0 = Y
'Etape 1.1 For h = 1, 2, ... ,
rang(X)
(a) Calculer les p-vector wh =
[w1h · ·
· wph]' o`u
wph = Cov(xph, yh)/ E
Cov2(xph, yh)
et xph la
pe
p
colonne de xh
(b) Normer wh : wh = wh/ II wh
II
(c) Calculer les variables latentes
t(m)
h = xh-1wh
(d) Calculer ch par regression GLS de
yh-1 sur t(m)
h
|
yh-1 =
t(h
m)ch + yh o`u
Var(yh-1) = V(m)
=
|
Er
k=0
|
ZkÄk
Z'kó2k m)
|
ch =(t(h
m)'V-1(m)t(hm))-t(h
m)'V-1(m)yh-1
(e) Calculer ph par regression de
xh-1 sur t(m)
h
xh-1 =
t(h
m)p'h+
xh p'h
=(t(h
m)'t(hm)
)-1t(h
m)'xh-1
(f) Calculer les residus xh and yh
(g)
Er
i=0
Ziui
Finalement Y =
T(m)C +
o`u T(m)
=[t(m)
1 ···t(h
m)] et C =
[c1 · · · ch]'
'Etape 1.2 Calculer
2m+1)
ók( =
ó2k (m)
(ók (m) / qk)
[YP(m) Z k
Ä'kZ'kP(m)Y
- tr(Z'kV -1(m)
Zk k)1
o`u P(m) =
V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)
'Etape 2 Si convergence, prendre
bó2k =
ó2k(m+1) ; sinon ajouter
1 a` m
et retourner a` 'Etape 1.1
Bien evidemment, le changement par rapport a` l'algorithme de
la section precedente concerne l''Etape 1.1 (d) et l''Etape 1.2 o`u
l'estimation des
ó2k tient compte de la
variance ó2kÄk des
effets aleatoires uk.
En resume, les estimations dans le mod`ele PLS-Mixte a` effets
aleatoires
corr'el'es ont ete'ecrites de mani`ere explicite. Neanmoins, pour
l'algorithme
itératif proposéa` cet effet, la convergence n'a
pas étéétablie et est restée locale.
| 


