Prédiction de l'interaction génotype à— environnement par linéarisation et régression PLS-mixte

4.3.1 La méthode PLS-Mixte sur un modèle a` effets aléatoires indépendants de variances homogènes

Nous nous plaçons dans le cadre du modèle 4.2 et considérons que n < p. Nous proposons la méthode PLS-Mixte qui consiste donc a` imbriquer une méthode de réduction de dimension telle que la régression PLS dans l'algorithme EM. Cette méthode d'estimation est fondée sur ML et ses variantes. L'estimation par ML est réalisée en maximisant la vraisemblance de Y par rapport aux paramètres inconnus.

Suivant l'algorithme EM, nous prenons des valeurs de départ pour les paramètres inconnus. Ces valeurs permettent de calculer les variables latentes obtenues a` partir du modèle (X, Y) vu que la variance V⁽⁰⁾ est connue, les valeurs initiales ó2(0)

k étant choisies. Sur ces variables latentes, sont calculées les composantes de varianceó²⁽¹⁾

k comme dans le cas classique de l'algorithme

EM. Avec les valeurs ó2(1)

k , ces étapes sont répétées avec les composantes ó2(0)

k

remplacées par les estimations courantes ó2(1)

k . Ce processus itératif est alors

continuéjusqu'àconvergence. Nous décrivons ci-dessous l'algorithme de la méthode proposée avant de le détailler plus loin.

'Etape 1 ('Etape-E) Centrer et reduire X et Y

'Etape 1.1 Reduire la dimension de l'espace des regresseurs en

determinant les h variables latentes T^(m) = [t^(m)

1 · · · t⁽_h :^m)]

vu que la variance V^(m) est connue 'Etape 1.2 Calculer

Q(ó² | ó2(m))

=E_ó2(m)(u^'iuk | Y)

= qkó2(m) k + ó4^(m) [Y^'P^(m)ZkZ^'kP^(m)Y - tr(ZkV^-1(m)Zk)1

o`u P^(m) = V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)

'Etape 2 ('Etape-M) Determiner ^ó2k(m+1) qui maximise E_ó2(m)(u^'iuk | Y) c`ad, tel

que QT(m)(ó^2(m+1) | ó2(m)) % QT(m)(ó² | ó2(m))

_ók2(m+1)

= E_ó2(m)(u^'iuk | Y)/qk pour k = 0, 1, · ··, r

'Etape 3 Si convergence, prendre bó²k = ók2(m+1) et alors calculer

X^-â = X(X^'V-^1(m+1)X)-X^'V-^1(m+1)Y

sinon ajouter 1 a` m et retourner a` 'Etape 1.

Les variables latentes sont ainsi recalculees au debut de chaque iteration dans l'algorithme EM avec les composantes de variance mises a` jour. Cet algorithme de la methode PLS-Mixte fondee sur une variation de ML est detaillede la facon suivante.

'Etape 1 Centrer et reduire X et Y : x0 = X, y0 = Y

'Etape 1.1 Pour h = 1,2, ... , rang(X)

(a) Calculer les p-vector wh = [w¹_h · · · w^p_h]^'

o`u w^p_h = Cov(x^p_h,yh)/ E Cov²(x^p_h, _yh) et x^p_h la p^e

p

colonne de xh

(b) Normer wh : wh = wh/ II wh II

(c) Calculer les variables latentes t(m)

h = xh-1wh

(d) Calculer ch par regression GLS de yh-1 sur t(m)

h

yh-1 = t^(h^m)ch + yh o`u Var(yh-1) = V(m) =

Xr k=0

ZkZ^'kók^2(m)

ch =~t(m)'

h _V-1(m)_t(m) ~-_t(m)'

h V-1(m)yh-1

h

(e) Calculer ph par regression de xh-1 sur t(m)

h
_~-1_t(m)'

xh-1 = t(m)

h p' h + xh d'o`u p' h =~t(m)'

h t(m) h xh-1

h

(f) Calculer les residus xh and yh

(g)

_Xr
i=0

Ziui

Finalement Y = T^(m)C +

o`u ^T(m) =[t^(m)

1 ···t(h ^m)] et C = [c1 · · · ch]^'

'Etape 1.2 Calculer

2m+1)

ó_k⁽ = C r k 2(m) + (ó k(m) / qk) [Y^'P^(m) Z kZ^'_kP^(m)Y - tr (Z'kV -1(m) Zk)1

o`u P^(m) = V-1(m)-V-1(m)T(m)(T(m)'V-1(m)T(m))-T(m)'V-1(m)

'Etape 2 Si convergence, prendre bó2k = ó2k(m+1) ; sinon ajouter 1 a` m

et retourner a` l''Etape 1.1

La procedure REML, quant a` elle, maximise la vraisemblance de certaines combinaisons lineaires des elements de Y par rapport aux param`etres inconnus (McCulloch and Searle, 2001). Notre methode fond'ee sur cette procedure REML est effectuee en remplacant l''Etape 1.2 par

2(m+1)

ó_i = ó^(m) + (ó4^(m) /qi) [Y^'P^(m)ZiZ^'_iP^(m)Y - tr(Z^'_iP^(m)Zi)]

o`u P^(m) reste defini comme ci-dessus.

Convergence de l'algorithme de la m'ethode PLS-Mixte :

Les proprietes de convergence de l'algorithme EM restent valides avec cette methode PLS-Mixte, en particulier sa convergence monotone. Par exemple, pour la monotonocitede l'algorithme EM, nous devons montrer que la fonction de vraisemblance, L(ó² | Y) ne decroit pas apr`es une iteration, c'est-`adire,

LT(m)(ór^m+1) | Y) LT(m-1)(ói ^2(m)| Y) (4.3)

o`u la valeur de la vraisemblance LT(m)(ó<sup>2(m+1)</sup> | Y) est calculee a` la (m + 1)^e

i

iteration en utilisant les valeurs actuelles de T^(m) comme regresseurs et la valeur de la vraisemblance LT(m-1)(ói 2(m) | Y) calculee a` la m^e iteration avec les valeurs de T(m-1)

Pour l'algorithme EM classique, le fait que la vraisemblance augmente a` chaque iteration est un resultat bien connu qui a etemontrepar Dempster, Laird et Rubin (1977) et discuteplus tard par Wu (1983) et par McLachlan et Krishnan (1997).

Nous nous sommes fond'es sur ce resultat pour montrer l'inegalite(4.3). La fonction de densiteconditionnelle des donnees compl`etes [Y, u<sup>'</sup>] o`u u^' = [u^' ₁,· · · ,u^'_r] sachant les donnees incompl`etes Y est egale a`

k([Y,u^'] | Y, ó²) = f[Y,u^']([Y,u^'] | ó²)

f(Y | ó²)

(4.4)

Alors la fonction log-vraisemblance des donnees incompl`etes peut s'ecrire comme suit :

l(ó² | Y) = ln (f(Y | ó²))

= ln (f[Y,u^']([Y, u^'] | ó²)/k([Y, u^'] | Y, ó²))

= ln (f[Y,u^']([Y, u^'] | ó²)) -- ln (k([Y, u^'] | Y, ó²)) = l[Y,u^'](ó² | [Y, u^']) -- ln(k([Y,u^'] | Y, ó²))

L'esperance de cette equation est prise par rapport a` la distribution conditionnelle des donnees compl`etes sachant les donnees incompl`etes, et en utilisant <sup>ó2(m)</sup> a` la place de ó². Ainsi,

E_ó2[l(ó² | Y) | Y1 = lT(m-1)(ó² | Y) (4.5)

= IE_ó2(m) [l[Y,u^'](ó² | [Y,u^']) | Y1

--E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y, ó²)) | Y1

Nous avons, a` l''Etape-E de l'algorithme du mod`ele PLS-Mixte avec une variance connue (section 2.2), la relation suivante :

E_ó2(m) [l[Y,u^'](ó² | [Y,u^']) | Y1 =E_ó2(u^'u | Y)

= QT(m-1)(ó² | ó2(m))

et en posant

GT(m-1)(ó² | ó2(m)) = [E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y,ó²)) | Y1

l'equation (4.5) devient

lT(m-1)(ó² | Y) = QT(m-1)(ó² | ó2(m)) -- GT(m-1)(ó² | ó2(m))

Nous pouvons maintenant calculer

lT(m)(ó^2(m+1) | Y) - lT(m-1)(ó^2(m) | Y) = QT(m)(ó^2(m+1) | ó2(m))

- GT(m)(ó^2(m+1) | ó2(m))

- QT(m-1)(ó^2(m) | ó2(m)) +GT(m-1)(ó^2(m) | ó2(m))

La quantit'e QT(m)(ó^2(m+1) | ó^2(m))-QT(m-1)(ó^2(m) | ó2(m)) est positive car ó2(m+1)

est choisie tel que

QT(m)(ó^2(m+1) | ó2(m)) = QT(m-1)(ó² | ó2(m)) ? ó2

Et, ? ó2

GT(m-1)(ó² | ó2(m)) - GT(m-1)(ó^2(m) | ó2(m)) = E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y, ó²)) | Y]

-E_ó2(m) [ln(kT(m-1)([Y,u^'] | Y,ó^2(m))) | Y]

= ln(1)

= 0

Ce r'esultat est montr'e par McLachlan et Krishnan (1997) pour l'algorithme
EM classique o`u les r'egresseurs sont consid'er'es comme fixes. Ici, la quantit'e

GT(m-1)(ó² | ó2(m)) - GT(m-1)(ó^2(m) | ó2(m))

est prise, ? ó², par rapport aux màemes r'egresseurs T^(m-¹⁾. Ce qui ne change donc pas le r'esultat.

Nous avons alors

lT(m)(ó^2(m+1) | Y) - lT(m-1)(ó^2(m) | Y) ~ 0

La m'ethode PLS-Mixte, utilise entre autres, la technique de r'eduction de dimension. Et dans ce sens, il faudra d'eterminer la dimension du modèle retenue. Pour cela, nous choisissons un nombre maximum h (h < rang(X)) de variables latentes au d'epart. La m'ethode it'erative d'ecrite plus haut permettra de calculer et d'actualiser tour a` tour ces h variables latentes et les composantes de variance. Avec ces composantes de variance estim'ees au final sur le modèle a` h variables latentes, les PRESS, Prediction error sum of squares (Stone 1974), des h sous-modèles avec respectivement 1, 2,
·
·
·, h r'egresseurs sont calcul'es. La dimension retenue est celle du sous-modèle a` plus faible PRESS.

Illustration avec des données de NIRS

Les algorithmes pr'esent'es ci-dessus sont test'es et appliqu'es a` titre illustratif sur un jeu de donn'ees de Rami, Dufour, Trouche, Fliedel, Mestres, Davrieux, Blanchard et Hamon (1998).

Il s'agit d'une population de lign'ees recombinantes de sorgho 'etudi'ee a` la station exp'erimentale de l'INERA au Burkina Faso. Cette population est obtenue par une m'ethode »modified single-seed descent» avec le g'enotype IS 2807 (collection de l'ICRISAT) consid'er'e comme femelle crois'ee avec le g'enotype 249 (collection du CIRAD) consid'er'e comme màale. Cette population de 90 individus fut r'ecolt'ee en 1995 a` la g'en'eration F7, a` partir d'un dispositif exp'erimental en lattice 9x10 avec trois r'ep'etitions.

Nous avons seulement retenu la teneur en prot'eine parmi un ensemble de mesures biochimiques effectu'ees sur les lign'ees, pour nous conformer aux conditions de notre m'ethode; c'est-à-dire qu'il n'est consid'er'e qu'une seule variable a` expliquer.

Pour cette teneur en prot'eine, il a 'et'e utilis'e une m'ethode traditionnelle de mesure, fiable mais longue a` effectuer; les valeurs mesur'ees sur toutes les lign'ees constituent le vecteur Y.

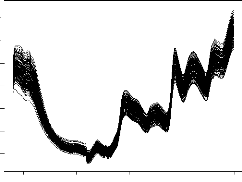
Parallèlement a` cette m'ethode de mesure, la technique NIRS, Near infrared reflectance spectroscopy, beaucoup plus rapide a 'et'e effectu'ee; les spectres d'absorption obtenus pour 1050 longueurs d'onde constituent la matrice X. La s'erie de longueurs d'onde consid'er'ee est constitu'ee d'une s'equence de 400 a` 1098 par 2 (figure 4.1).

FIG. 4.1 - Spectres d'absorption proches de l'infrarouge pour une population de lignées de sorgho récoltées en 1995 a` la Station expérimentale de l'INERA au Burkina Faso.

500 1000 1500 2000 2500

absorbance

0.1 02 0.3 0.4 0.5 0.6 0.7

longueurs d'onde

Au delàde notre souci d'utiliser ces donn'ees pour tester et 'eprouver notre m'ethode, l'int'erêt de cette 'etude chez le praticien, pourrait être de calibrer la technique NIRS sur le sorgho pour la teneur en prot'eine dans le but d'obtenir une m'ethode de mesure rapide en tenant compte de la structure particulière de la covariance des erreurs induite par le dispositif exp'erimental.

Pour la mise en oeuvre de la m'ethode PLS-Mixte sur ces donn'ees, il existe cependant des donn'ees manquantes a` savoir la troisième r'ep'etition et trois lign'ees des deux autres r'ep'etitions. Eu 'egard au nombre important de longueurs d'onde (1050) et la corr'elation massive habituellement constat'ee sur les donn'ees de NIRS, nous avons d'ecid'e de conserver syst'ematiquement une longueur d'onde toutes les cinq.

Le modèle consid'er'e pour ces donn'ees s''ecrit comme suit :

Y = Xâ + _Z1u1 + _Z2u2 + e (4.6)

o`u u1 d'ordre 2 est l'effet al'eatoire de la r'ep'etition et u2 d'ordre 20 l'effet al'eatoire du bloc hi'erarchis'e dans la r'ep'etition.

Finalement, la dimension de Y est 174×1 et la dimension de X est 174×210. Aussi, Z1 est une matrice 174×2 et u1 un vecteur 2×1 tandis que Z2 est une matrice 174×20 et u2 un vecteur 20×1.

Les hypothèses pour ce modèle sont par cons'equent

? ???? ????

u1 ~ N(0,ó^21I2) u2 ~ N(0, ó2 2I20) u0 ~ N(0,ó^2 0I174) avec u0 = e

Nous avons donc pour ce modèle, plus de r'egresseurs que d'observations (210 contre 174) et trois composantes de variance a` estimer (ó<sup>2</sup><sub>1</sub> pour l'effet al'eatoire de la r'ep'etition, ó2 2 pour l'effet al'eatoire du bloc et ó2 0 pour l'erreur r'esiduelle al'eatoire). Nous allons donc avoir recours a` la m'ethode PLS-Mixte fond'ee sur ML et sur REML pour estimer les quatres paramètres â, ó² 1, ó2 2 et ó² ₀.

Pour le calcul du PRESS, nous avons, comme annonc'e plus haut, choisi un
nombre maximum de 10 variables latentes. Avec un modèle de dimension 10,

nous avons utilis'e la m'ethode PLS-Mixte pour estimer les trois composantes de variance. Par la suite, pour chacun des sous-modèles de dimension 1 a` 10, nous avons enlev'e successivement chaque lign'ee (dans les deux r'ep'etitions) dont nous avons pr'edit sa teneur en prot'eine par les lign'ees restantes en utilisant une r'egression GLS avec les composantes de variance estim'ees sur le modèle de dimension 10.

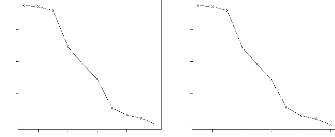
Le PRESS d'ecroàýt continuellement avec le nombre de variables latentes pour les deux modèles fond'es sur ML et sur REML quand le nombre de composantes maximum avait initialement 'et'e fix'e a` 10. Cependant, nous avons d'ecid'e pour ces modèles de r'eduire leur espace a` 7 dimensions 'etant donn'e que le PRESS n'y est pas trop diff'erent de ses valeurs minimales (figure 4.2).

FIG. 4.2 - 'Evolution du PRESS selon le nombre de variables latentes quand le nombre maximal de variables latentes avait initialement étéfixéa` dix pour les données de NIRS.

ML REML

PRESS

20 25 30 35

2 4 6 8 10

2 4 6 8 10

20 25 30 35

PRESS

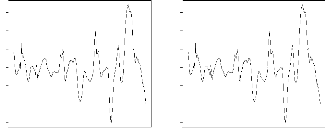
Par rapport a` l'objectif de cette 'etude, il serait question de s'electionner les r'egresseurs influents. Nous pouvons alors pour cela, consid'erer les coefficients les plus grands en valeur absolue des r'egresseurs pour le modèle s'electionn'e. Nous notons ainsi que les bandes d'absorption localis'ees autour de 2210, 1940, 1690 et 1450 ont les plus grands coefficients (figure 4.3).

FIG. 4.3 - 'Evolution des coefficientsâ^b (modèle (4.6)) selon les différentes longueurs d'onde pour les modèles a` 7 variables latentes fondés sur ML et REML des données de NIRS.

ML REML

.9 02

02

0.0 0.1

-0 -02 .1 -0

-0.9

02

02

00 0.1

-02 -0.1

500 1000 1500 2000 2500 500 1000 1500 2000 2500

wavelengths wavelengths

Les estimations de ó _k pour ML et pour REML sont montr'ees au tableau 4.1. Nous notons que la variance de l'effet bloc hi'erarchis'e dans la r'ep'etition est deux fois plus faible que celle de l'effet r'ep'etition.

ML REML

ó ₁ 0,11273 0,11276
ó 0,06248 0,06309
ó ₀ 0,46839 0,48917

Estimation des composantes de variance pour les modèles a` 7 va-

TAB. 4.1 - riables latentes fondés sur ML et REML des données de NIRS.

Au tableau 4.2, nous avons le MSEP du modèle 4.6 analys'e par r'egression PLS et le MSEP du même modèle analys'e par la m'ethode PLS-Mixte fond'ee sur ML et sur REML. La pr'ediction par la m'ethode PLS-Mixte, comme nous nous y attendons, de la teneur en prot'eine du sorgho par les bandes d'absorption, quand il y a plusieurs sources de variation, est meilleure que celle faite par simple r'egression PLS.

MSEP

ML 0,64637

PLS-Mixte REML 0,64639

PLS 0,91479

TAB. 4.2 - MSEP des modèles de la méthode PLS-Mixte et de la régression PLS pour les données de NIRS.

Toutefois, la détermination de la dimension optimale a` travers le calcul du PRESS est ici liée a` h, le nombre maximum de variables latentes choisi au départ. En effet, les composantes de variance sont estimées avec les h variables latentes et utilisées par la suite respectivement pour chaque sous-modèle a` 1, 2, ..., h variables latentes pour estimer â et finalement pour calculer les PRESS. Cependant, le choix de h semble ne pas avoir un impact important sur le calcul des PRESS dans notre example. A la figure 4.4, nous avons présentéles valeurs des PRESS calculées pour un nombre maximum de variables latentes choisi initialement pour être égal respectivement a` 10, 20, 30, 40 et 50. L'évolution du PRESS jusqu'àla dixième variable latente n'est quasiment pas affectée par le choix initial du nombre maximum de variables latentes.