I.
Le symbole ? designe le produit de Kronecker.
Le vecteur o est un vecteur d'erreur aleatoire. Sa matrice de
covariance est de la forme
ó2uÙ
avec
|
|
?
? ? ? ? ? ? ? ? ?
|
ù1
|
..
|
.
|
|
|
0
|
1
|
|
Ù=
|
|
|
|
ùj
|
|
|
|
o`u
|
|
0
|
|
|
|
...
|
ùJ
|
(
ùj =
Les matrices Ù et ùj sont
carrees de nombre de lignes, respectivement le nombre d'observations de tous
les environnements et le nombre d'observations de l'environnement
j. La matrice Ù est bloc diagonale tandis que
ùj est une matrice form'ee de 1 partout sauf des 2 sur
la diagonale. Dans le cas o`u tous les genotypes ont etevus une seule fois dans
chaque environnement, Ù est de dimension IJ
× IJ et ùj de dimension I ×
I.
Ensuite,
X = [ X(1) ? II · ·
· X(p) ? II ·
· · X(P) ?
II
o`u
X(p)' = [
X1p) ...
XSp) ]
de longueur J, est le vecteur des derivees
des sorties de notre modele de simulation de cultures, SarraH, dans chacun des
environnements par rapport au pe parametre du
vecteur de parametres du temoin.
La matrice II est la matrice
identited'ordre I, la matrice
X(p) 0II
s'ecrit alors de cette facon :
|
X(p)
1
...
X(p)
(
J )
|
0
|
(
|
1
.
0
|
0
..
1
|
)
|
=
|
X(p)
1
?
0
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
X(p)
J
0
|
...
...
0
?
X(p)
1
...
0
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
X(p)
J
|
C'est une matrice a` IJ lignes et
I colonnes. Par consequent, la matrice X est de
dimension IJ x PI.
Enfin
â = [ â(1)'
...â(P)' 1'
avec
â(p)' = [
â1.p) ...
â(p) ]
Nous avons proposed'appeler cette methode par l'acronyme APLAT
: Ap-
proximation Par Linearisation Autour d'un Temoin. Elle consiste a`
appro-
cher, localement, le rendement predit par un modele de simulation de
cultures,
par s'erie de Taylor a` l'ordre 1 au voisinage du vecteur de
paramètres d'un g'enotype de r'ef'erence. Cette lin'earisation permet,
par r'egression lin'eaire, l'estimation des paramètres de ces
g'enotypes. Par la suite, la pr'ediction de l''ecart entre le rendement de ces
g'enotypes et celui du g'enotype de r'ef'erence dans des environnements
nouveaux, c'est a` dire o`u ils ne sont pas encore test'es, pourra se faire si
le climat de ces derniers est connu.
Il y a en g'en'eral beaucoup de paramètres dans un
modèle de simulation de cultures et peu d'environnements dans un essai
multienvironnement, ce qui rend souvent PI grand par rapport
a` IJ.
Pour notre exemple, nous avons utilis'e SarraH comme
modèle de simulation de cultures. Ce modèle dispose de 61
paramètres fonction du g'enotype. Avec un tel nombre de pr'edicteurs,
l'estimation de â s'est faite par r'egression PLS. Ceci permet de
r'eduire l'espace des r'egresseurs de rang de X a` k
dimensions.
La r'egression PLS, voir section 3.1, s'effectue selon le
principe de l'algorithme NIPALS, Nonlinear estimation by Iterative
Partial Least Squares, (Tenenhaus, 2001) o`u un ensemble de
r'egressions successives par moindres carr'es ordinaires est effectu'e, en
même temps que le calcul des composantes.
Ici, la matrice de covariance de o est 'egale a`
ó2
uÙ et non a` ó2
uIIJ. La solution serait d'effectuer toutes les r'egressions
partielles par moindres carr'es g'en'eralis'es. Mais cette matrice de
covariance est inconnue. Elle s''ecrit tout de même a` une constante
multiplicative près en fonction de Ù qui elle
est connue. La matrice Ù 'etant sym'etrique et
semi-d'efinie positive, par d'ecomposition de Cholesky, il existe une matrice
ç tel que ç'ç =
Ù-1.
Si nous multiplions a` gauche tous les termes du modèle
3.5 par ç, nous obtenons le modèle 3.6 dont les erreurs sont
ind'ependantes.
çY - ç(Y0
? 1I) = çX · â +
ço (3.6)
En effet, la variance de l'erreur ço s''ecrit
uçç-1(ç')-1ç'
= ó2
E(çoo'ç')
=
çI(oo')ç'
= ó2
uçÙç' =
ó2
uç(ç'ç)-1ç'
= ó2 uIIJ
â peut alors être estim'e a` l'aide des moindres
carr'es ordinaires, appelons âPLS
son estimateur.
Le nombre de composantes a` retenir est d'etermin'e par le PRESS,
Prediction Error Sum of Squares (Tenenhaus, 2001).
3.2.2 Illustration avec les données de l'essai
pluriannuel
Les données
Les donn'ees sont les r'esultats de l'essai pluriannuel
(tableau 1.1, page 13). Rappelons que le g'enotype de r'ef'erence est le
55-437, un g'enotype de 90 jours. C'est une vari'et'e
largement cultiv'ee au S'en'egal, dans le bassin arachidier, a` ce titre elle a
'et'e pr'esente comme t'emoin dans tous les essais et c'est elle aussi qui a
servi pour le param'etrage du modèle SarraH.
Dans ce milieu a` forte variabilit'e des pluies dans l'espace
et même dans le temps pour un même lieu, nous avons consid'er'e
chacune des 5 ann'ees d'exp'erimentation comme un environnement (figure
3.1).
SarraH a 'et'e utilis'e pour calculer X.
Compte tenu du nombre de donn'ees disponibles, seuls deux paramètres
(P = 2) ont 'et'e consid'er'es parmi les 61 de SarraH. Le
premier paramètre est en fait un coefficient multiplicateur qui agit sur
5 paramètres de SarraH : Coefficient moyen d'angle des feuilles,
Coefficient de conversion en assimilat, Coefficient d'efficience d'assimilation
des feuilles a` la phase v'eg'etative juv'enile, Coefficient d'efficience
d'assimilation
FIG. 3.1 - R'epartition des pluies sur la station de
Bambey au S'en'egal de 1994 a` 1998.
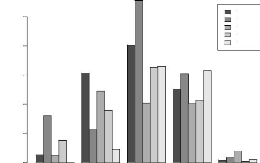
MIT
0 50 100 150 200 250
1994 1995 1996 1997 1998
Juin Juillet Août Septembre Octobre
des feuilles a` la première phase de maturation - phase
sensible de remplissage des grains - et Coefficient d'efficience d'assimilation
des feuilles a` la deuxième phase de maturation - phase non sensible -.
Le deuxième paramètre est le poids moyen des gousses.
Validation croisée
Pour valider notre modèle, nous avons r'eserv'e
successivement chacune des ann'ees et estim'e les paramètres des
g'enotypes sur les ann'ees restantes. Pour chacune des cinq ann'ees, nous avons
identifi'e un modèle par la m'ethode APLAT et les rendements observ'es
ont 'et'e compar'es a` ceux ainsi pr'edits. Les rendements sont exprim'es en
kilogrammes de gousses par hectare.
L''evaluation de la qualit'e de chaque modèle propos'e
est faite avec l'erreur
quadratique moyenne de pr'ediction MSEP,
Mean Squared Error of Prediction
(Wallach et Goffinet, 1987). La MSEP est utilis'ee comme
critère pour comparer diff'erents modèles dont le mod`ele moyen
(Colson, Wallach, Bouniols, Denis et Jones, 1995) d'efini pour nos donn'ees par
:
Yij = m + gi + Ej + äij (3.7)
o`u m est la moyenne de la population
et gi l'effet g'enotype. L'effet Ej de
l'environnement j est suppos'e al'eatoire, d'esp'erance nulle
et de variance
ó2E. Les erreurs
äij sont ind'ependantes, d'esp'erance nulle et de
variance ó2ä. De
plus, Ej et äij sont suppos'es
ind'ependants.
Le modèle moyen n'est rien d'autre que le modèle
lin'eaire mixte (2.1) o`u l'interaction al'eatoire G×E,
impr'evissible, est fusionn'ee avec le terme d'erreur qui porte les
màemes indices i pour le g'enotype et
j pour l'environnement.
Nous avons calcul'e les intervalles de confiance des
coefficients estim'es par la m'ethode bootstrap (Efron, 1979).
Cette technique permet d'estimer la loi inconnue d'un estimateur par une loi
empirique obtenue a` partir d'une proc'edure de r'e'echantillonnage fond'ee sur
des tirages al'eatoires avec remise des donn'ees. Les intervalles de confiance
construits sont de type percentile-t (Aji, Tavolaro, Lantz, et
Faraj, 2003).
Soit z(p)?b
i,PLS la variable al'eatoire d'efinie par :
(p)?b
zi,PLS
=
(3.8)
ei?LbS)
â(p)?b
i,PLS- 7A,S
s?(
o`u
â(p)i,PLS est le
(p.i)e 'el'ement de
eâPLS, il s'agit du pe
paramètre de la ie vari'et'e
estim'e par
la m'ethode PLS. gL?bS est obtenu
au be tirage avec b =
1,
·
·
· , B.
|
de la matrice de variance de
|
â(p)?b
i,PLS.
|
Soit bFB la fonction
de répartition empirique des z(pP
)?b Le fractile d'ordre á,
i LS'
1
B
XB
b=1
FB (á) est
estimépar la valeur
bt(á) telle que
1n = á
z(p)?b
Alors un intervalle de confiance percentile-t
pour le (p.i)e élément de
13 peut s'écrire :
hs(â(p)i,PLS)
t(1 - á) , /R1,3P)LS -
s(â(p)i,PLS) ·
Rá) ] (3.9)
R'esultats
Pour les modeles sans les données respectivement de
1994, 1995 et 1997, le PRESS minimal est atteint avec 6 composantes. Pour les
deux autres modeles, le PRESS est minimal avec 9 composantes, mais nous avons
réduit leur espace a` 5 dimensions car le PRESS n'y est pas trop
différent de ses valeurs minimales (figure 3.2).
Les coefficients des régressions PLS et les intervalles de
confiance qui leur sont associés, sont représent'es a` la figure
3.3.
Les MSEP estimées pour les modeles APLAT, sauf celle
sans les données de l'année 1998, sont inférieures aux
MSEP des modeles moyens correspondants (tableau 4.2). Ce qui signifie que pour
ces modeles, prédire le rendement par la méthode APLAT est
meilleur que par la moyenne des rendements du passé. Ainsi, 4 fois sur
5, la méthode APLAT s'est révélée meilleure que le
modele moyen. Toutefois, cette étude souffre de la faible taille de
notre échantillon.
Evolution du PRESS en fonction du nombre de composantes.
Le FIG. 3.2 - modèle (-1994) utilise les données
sauf celles de l'année 1994 et ainsi de suite.
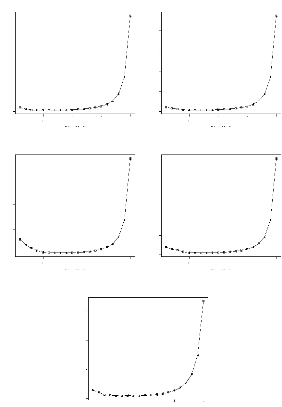
PRESS
0.0 0.5 1.0 1.5 2.0 2.5
PRESS
Modèle (-1994) : Dim. opt. 6,
PRESS=0.051
5 10 15 20
Dim. Mod.
Modèle (-1996) : Dim. opt. 9,
PRESS=0.037
5 10 15 20
Dim. Mod.
Modèle (-1995) : Dim. opt. 6,
PRESS=0.061
5 10 15 20
Dim. Mod.
Modèle (-1997) : Dim. opt. 6,
PRESS=0.034
5 10 15 20
Dim. Mod.
Modèle (-1998) : Dim. opt. 9,
PRESS=0.046
5 10 15 20
PRESS
0.0 0.5 1.0 1.5
PRESS
0.0 0.5 1.0 1.5
PRESS
Dim. Mod.
Intervalle de confiance percentile-t a` 95% des
coefficients es-
timés. Le modèle (-1994) est
sans les données de 1994 et ainsi
FIG. 3.3 - de suite. Sur l'axe des abscisses, les valeurs
de chaque paramètre sont rangées par ordre
alphabétique de génotype. Le symbole
représente l'estimation ponctuelle des coefficients.
0.5 1.0 1.5 2.0 2.5
3
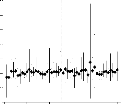
Paramètre 1 Paramètre 2
Modèle (-1994)
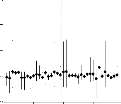
Paramètre 1 Paramètre 2
010 20 30
Modèle (-1996)
Modèle (-1995)
0 10 20 30
Modèle (-1997)

0 10 20 30 50 0 10 20 30
-0.5 0.0 0.5 1.0 1.5 2.0
Modèle (-1998)
Paramètre 1 Paramètre 2
50
40
30
0 10 20
|
APLAT
|
Modèle moyen
|
|
Modèle (-1994)
|
24
|
687,3
|
64
|
651,6
|
|
Modèle (-1995)
|
5
|
915,0
|
7
|
160,6
|
|
Modèle (-1996)
|
35
|
446,1
|
37
|
814,8
|
|
Modèle (-1997)
|
10
|
038,3
|
18
|
201,1
|
|
Modèle (-1998)
|
118
|
304,9
|
84
|
963,6
|
MSEP des différents modèles APLAT et
modèles moyens corres-
TAB. 3.1 - pondants de l'essai pluriannuel. Le
modèle (-1994) est sans les données de 1994 et ainsi de
suite.
| 


