Géomarketing : localisation commerciale multiple

2.3 Limitations du modèle p-médian et de ses méthodes actuelles de résolution

2.3.1 Le modèle p-médian : une réalité simplifiée

Le modèle p-médian est uniquement axé, comme nous l'avons précisé, sur les notions de distance et de demande dans le cas du modèle p-médian pondéré. Mais, même si le propos n'est pas fondamentalement de critiquer le modèle lui-même, il est évident que le

⁵³¹ ARMSTRONG J.S. et BRODIE R.J. (1994) Effects of Portfolio Planning Methods on Decision Making : Experimental Results, International Research Journal in Marketing 11, North-Holland, 73-84.

⁵³² KOLEN A. et TAMIR A. (1990) Covering Problems, Discrete Location Theory de Mirchandani & Francis

Chap. 6, Wiley & Sons.

consommateur ne se fondera pas seulement sur le seul critère de distance pour choisir son point de vente parmi un éventail de concurrents. Les autres paramètres jouant sur la décision des clients peuvent être formulés sous forme de cinq principes qui guideront la sélection des emplacements commerciaux^{533 534}:

- le principe d'interception: le point de vente a d'autant plus de chance de capter la clientèle

que le passage de consommateurs à proximité, mesuré le plus souvent en terme de trafic piétonnier ou routier, est important.

- le principe d'attraction cumulative: le regroupement de commerces dans un environnement géographique proche d'activités similaires crée souvent une synergie d'attractivité alors supérieure à la somme des attractivités individuelles des commerces.

- le principe de compatibilité: de même, le regroupement d'activités complémentaires permet assez souvent de parvenir à ce même effet synergique des attractivités.

- le principe de suréquipement: une trop grande concentration de points de vente a tendance à avoir un effet répulsif sur la clientèle alors soumis à l'inconfort de la congestion du trafic.

- le principe d'accessibilité: l'accessibilité au point de vente, c'est-à-dire la facilité d'entrer, de pénétrer, de traverser et de sortir du site commercial doit être le plus facile possible. Une bonne signalisation, la qualité et le nombre de voies d'accès, les facilités de parking sont autant de paramètres à privilégier dans le choix d'un emplacement convenable.

Une solution que nous proposons pour intégrer tous ces critères seraient d'introduire dans le

problème p-médian un poids évaluant chaque site potentiel. Rien n'empêche en effet de

mesurer et de quantifier pour chaque emplacement potentiel des points de vente les différents critères mentionnés tels que l'ont fait Lewison et Delozier⁵³⁵ et Jallais, Orsony et Fady ⁵³⁶.

⁵³³ DELOZIER M.W. et LEWISON D.M. (1986) Retailing, 2nd ed., Merill.

⁵³⁴ CLIQUET G. (1992) Le Management Stratégique des Points de Vente, p.187-191, Ed. Sirey.

⁵³⁵ DELOZIER M.W. et LEWISON D.M. (1986) Retailing, 2nd ed., Merill.

⁵³⁶ JALLAIS J., ORSONY J. et FADY A. (1994) Marketing du Commerce de Détail, Vuibert, Paris.

Puis il convient d'attribuer une note globale à chaque site potentiel, note résultant d'une pondération de ces critères. A titre d'exemple, il suffirait d'attribuer des notes par exemple de

0 (emplacement vraiment médiocre) à 100 (emplacement excellent) pour chaque critère, de

les pondérer avec des coefficients positifs de manière à quantifier leur importance et d'obtenir une note globale nj. Cette note introduite dans la fonction objectif avec un signe négatif (ayant tendance à minimiser avantageusement la fonction) au même niveau que les distances dij servirait de pondération à chaque site potentiel d'activité. La distance dij en tant que critère impliquant à la fois le commerce et le client considéré devrait alors être normalisée (sur la même échelle de notes) de manière à obtenir une homogénéité au sein de la fonction objectif.

La formulation mathématique du p-médian deviendrait alors:

Minimiser

^{i j}

ai (dij - nj) xij représente la nouvelle fonction objectif, (1)

avec

i

xij = 1, i, assure que tous les clients sont assignés à une activité et une seule, (2)

^{et d}ij ^{- n}j ^{0, j assure que toute activité possède un minimum d'attractivité, (2)'}

xij yj, i, j empêche d'assigner un client à une activité si elle n'est pas ouverte, (3)

yj = p, le nombre total d'activités est p, (4)

^j

^xij^{, y}j ^{{0,1}, i, j nature binaire des variables x}ij^{, y}j ⁽⁵⁾

où

ai : est la demande au noeud i,

nj: la note positive attribuée au site potentiel du noeud j, di,j : la distance du noeud i au noeud j,

p : le nombre d'activités à localiser,

xi,j = 1, si le noeud i est assigné à l'activité j et 0 autrement,

yj = 1, si l'activité j est ouverte et 0 autrement.

On observe que logiquement dans la fonction objectif, plus l'activité au noeud j est attractive

(note nij importante), meilleure est la fonction objectif (valeur plus faible) et que l'attractivité

est un réducteur de distance, la valeur (dij - nj) pouvant être qualifiée de "distance psychologique" qui est la distance ressentie effectivement par les consommateurs et non plus seulement la distance routière ou temporelle^{537 538}. Un autre avantage de cette nouvelle formulation que l'on pourrait qualifier de "modèle p-médian généralisé" est qu'elle est soluble

par les méthodes traditionnelles de résolution du p-médian puisque la forme de la fonction objectif est similaire (forme linéaire).

2.3.2 La complexité des méthodes de résolution du p-médian

L'autre reproche déjà évoqué au niveau du modèle p-MP concerne cette fois ses méthodes existantes de résolution. Celles-ci sont très lourdes et même souvent impossibles à mettre en oeuvre si l'on considère un réseau de plusieurs centaines de milliers de noeuds. Quelle tâche herculéenne que d'imaginer vouloir trouver une solution plus ou moins optimale à un réseau comprenant l'ensemble des clients potentiels d'une future grande surface ! Un autre problème

du même ordre, mais cette fois dans le domaine de la gestion informatique serait de considérer le réseau de communication Internet et les différents micro-ordinateurs, serveurs et réseaux Intranet le composant (soit des millions d'ordinateurs à travers le monde): sur quels serveurs (les noeuds d'activités) serait-il préférable de localiser les données pour que celles-ci soient acheminées le plus rapidement possible à destination des autres ordinateurs (les clients)

connaissant les probabilités de requête (les demandes ) ?

⁵³⁷ HUBBARD R. (1978) A Review of Selected Factors Conditioning Consumer Travel Behavior, Journal of

Consumer Research, vol. 5, june, p.1-21.

⁵³⁸ VOLLE P. (1999) Du Marketing des Points de Vente à Celui des Sites Marchands : Spécificités, Opportunités

et Questions de Recherche, Cahier n°276, Centre de Recherche DMSP, juin 1999.

Le problème classique du p-médian a pourtant fait couler beaucoup d'encre, en témoigne le

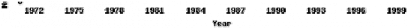
nombre d'articles où ce modèle est cité (en excluant les auto-citations):

Fig. 2.13 - Nombres d'articles traitant du p-médian par année - source: The Scientific Literature Digital Library

Les 225 articles cités sur 30 ans ne s'attaquent cependant qu'à l'affinage de la résolution du p- médian à savoir essentiellement améliorer l'optimalité des solutions à travers de nouvelles heuristiques d'amélioration (et rarement des algorithmes de résolution). Les autres publications de recherche traitent principalement des applications du p-MP en adaptant le modèle à certains cas particuliers comme l'efficacité des moteurs de recherche⁵³⁹, le coloriage

de graphes à l'aide du p-MP et d'un algorithme génétique⁵⁴⁰ ou encore la localisation de simulateurs de conduite de char de l'armée américaine au plus près des casernes⁵⁴¹.

2.3.3 L'analyse typologique : une approche pour simplifier la problématique du p-MP Peu d'articles abordent vraiment la partie fondamentale, mais ô combien stratégique de la formulation ou de la modélisation même du problème p-MP. Si elle est mieux établie, elle permettra de simplifier le problème et de parvenir à une solution plus rapidement ou à une

meilleure solution en utilisant un algorithme plus lent mais plus performant capable de traiter

⁵³⁹ CRASWELL N. et BAILEY P. (1999) Is it fair to evaluate Web systems using TREC ad hoc, Department of

Computer Science - CSIRO, The Australian National University Pub.

⁵⁴⁰ RIBEIRO FILHO G. et NOGUEIRA LORENA L.A. (2000) Improvements On Constructive Genetic

Approaches To Graph Coloring, Sao José Dos Campos, Spain.

⁵⁴¹ MURTY K.G. et DJANG P.A. (2000) The US Army National Guard's Mobile Training Simulator Location and Routing Problem, US Army Training and Doctrine Analysis Command, Dept. of IOE, University of

Michigan.

les modèles intégrant un très grand nombre de noeuds. Cependant, il est à noter qu'un problème assez étudié et à la mode est celui de l'analyse typologique (cluster analysis en anglais). Déjà évoqué par Aristote, cette dernière consiste à partitionner un ensemble d'entités

en sous-ensembles bien séparés et homogènes selon un certain nombre de paramètres. Dans le domaine de l'identification de classes, on peut recenser dans la littérature deux approches qui

se sont développées, la première étant celle de la reconnaissance déterministe et de décision

par sélection de distance; la seconde est statistique car elle a pour base des probabilités acquises lors d'une phase d'apprentissage et une décision par sélection de pénalisations

encourues. En particulier, la classification séquentielle utilisée par de nombreux chercheurs

dans les procédures de reconnaissance de forme se rattache à cette dernière approche^{542 543 544}

^{545 546 547 548}. Il existe également des méthodes de segmentation fondées sur un algorithme génétique associé à un modèle de régression⁵⁴⁹.

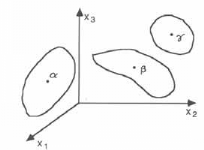
Fig. 2.14 - Un exemple de 3 classes , et identifiées par les variables x1, x2, x3

⁵⁴² DUDA R.O. et HART P.E. (1973) Pattern Classification and Scene Analysis Editions J. Wiley, New York, N.Y.

⁵⁴³ TOU J.T. et GONZALEZ R.C. (1974) Pattern Recognition Principles, Edition Addison-Wesley, Reading,

Mass.

⁵⁴⁴ FU K.S. (1968) Sequential Methods in Pattern Recognition and Machine Learning, Editions Academic Press, New York, N.Y.

⁵⁴⁵ PAVLIDIS T. (1977) Structural Pattern Recognition, Editions Springer-Verlag, New York, N.Y.

⁵⁴⁶ PATRICK E.A. (1972) Fundamentals of Pattern Recognition, Edition Prentice-Hall, Englewood Cliffs, N.J.

⁵⁴⁷ POSTAIRE J.G. (1987) De l'Image à la Décision, Editions Dunod-Informatique Bordas, Paris.

⁵⁴⁸ CHEN C.H. (1973) Statistical Pattern Recognition, Editions Spartan Books, Rochelle Park, N.J.

⁵⁴⁹ AURIFEILLE J.M. (2000) A Bio-mimetic Approach to Marketing Segmentation : Principles and

Comparative Analysis, European Journal of Economic and Social Systems 14 N°1, p. 93-108.

Si l'analyse typologique intéresse principalement le domaine des mathématiques statistiques, elle recense également des applications dans le domaine de la localisation et du problème p- médian⁵⁵⁰ (voir son utilisation au § 2.4.2.4. dans la délimitation des zones de chalandise). Un exemple récent est représenté par la décomposition de la Suisse ou plutôt des 2863 principales communes suisses en 23 cellules associées chacune à un centre urbain⁵⁵¹ selon diverses

méthodes comparées: p-médian, méthode Alt⁵⁵², algorithme de décomposition⁵⁵³. Le

problème est en premier lieu d'identifier les 23 centres urbains et d'y affecter ensuite des communes selon le critère du plus proche voisin en terme de distance à vol d'oiseau. Selon notre point de vue, cette analyse typologique géographique peut conduire en quelque sorte à une simplification du problème p-médian, dans le sens où, plutôt que prendre comme noeuds

du réseau l'ensemble des 2863 communes au sein desquelles on rechercherait une ou plusieurs localisations optimales, on pourrait plus aisément considérer les 23 centres urbains comme étant les noeuds d'un réseau p-médian simplifié: l'étape d'analyse typologique constituerait une étape amont destinée à constituer ce réseau p-médian simplifié (avec comme noeuds les 23 centres urbains) préalablement à sa résolution.

Mais, cette manière de simplifier le problème p-médian comporterait de nombreuses limitations dont celle en premier lieu de devoir spécifier à l'avance en combien de classes (et donc de noeuds du futur réseau p-médian simplifié) il conviendrait de partitionner l'ensemble des entités de départ: ainsi, dans le problème précédent, il a été fixé d'entrée de jeu de partitionner le territoire suisse en un nombre de 23 cellules associées à 23 centres urbains sans

que ce nombre ait été ultérieurement justifié.

⁵⁵⁰ ROGER P. (1983) Description du Comportement Spatial du Consommateur, Thèse de Doctorat, Lille.

⁵⁵¹ TAILLARD E.D. (1996) Heuristic Methods for Large Centroid Clustering Problems, Technical Report Idsia

96-96, Idsia.

⁵⁵² COOPER L.G. (1963) Location-Allocation Problems, Operations Research 11, 331-341.

⁵⁵³ TAILLARD E.D. (1996) Heuristic Methods for Large Centroid Clustering Problems, Technical Report Idsia

96-96.

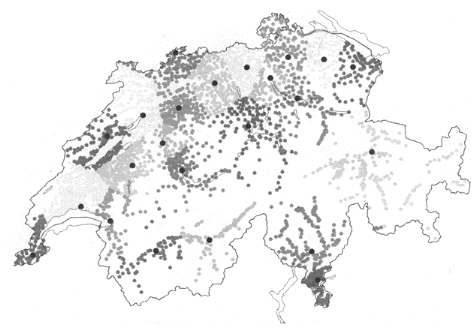
Fig. 2.15- Partition des communes suisses en 23 cellules représentées chacune par un centre urbain ⁵⁵⁴

Les exemples personnels suivants illustrent le principe de l'analyse typologique utilisée dans

le cadre du p-médian et l'erreur dans la recherche d'une localisation optimale qui peut résulter d'un nombre prédéfini de partitions. D'abord, un cas où l'approche de l'analyse typologique fonctionne bien: considérons 76 villes de même taille réparties sur un territoire, chaque ville étant représentée par un cercle :

⁵⁵⁴ TAILLARD E.D. (1996) Heuristic Methods for Large Centroid Clustering Problems, Technical Report Idsia

96-96, Idsia.

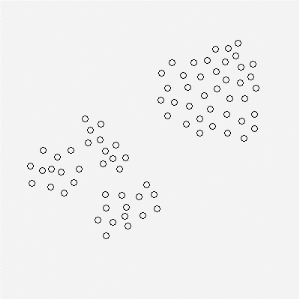
Fig. 2.16 - Les 76 villes représentées chacune par un cercle

Si l'on décide de partitionner l'espace géographique en deux par la méthode des k-plus proches voisins (k=2) par exemple, on aura deux régions A et B avec leurs centres respectifs,

les noeuds a et b:

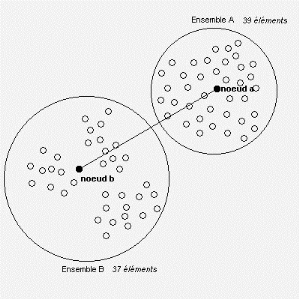
Fig. 2.17 - Partition des 76 villes en 2 ensembles

Prenons comme poids des noeuds a et b de ce réseau pondéré, l'importance de la population représentée respectivement par le nombre de villes des deux ensembles soit 39 villes et 37 villes. Alors la localisation optimale d'une activité unique selon le problème 1-médian sera choisie au noeud a car il a un coefficient de pondération plus important. Mais, si l'on choisit un nombre de partitions égal à 4, on obtient alors la répartition suivante avec chacun des noeuds reliés aux noeuds de ceux des autres ensembles les plus proches:

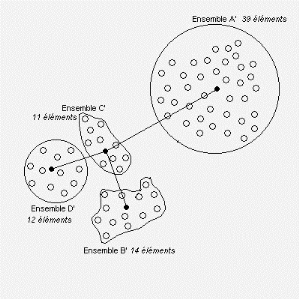
Fig. 2.18 - Partition des 76 villes en 4 ensembles

Le centre optimal est alors situé sur le noeud de l'ensemble A' qui correspond bien au noeud a

de l'ensemble A précédemment. Si on considère maintenant le contre-exemple suivant avec 3

partitionsde 17 villes, la droite verticale passant par O étant la droite médiane du segment ab:

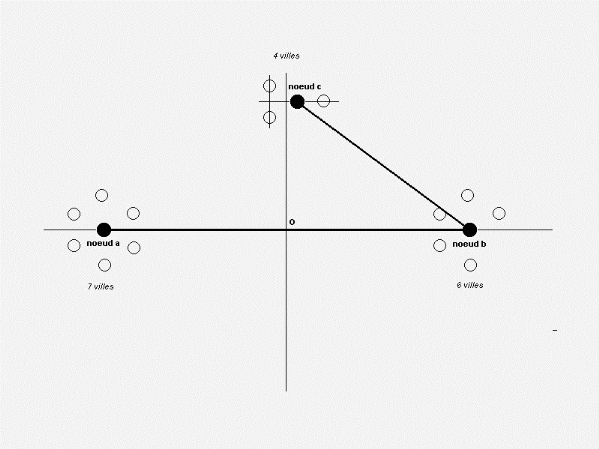
Fig. 2.19 - Partition de 17 villes en 3 ensembles

Selon le modèle 1-médian, le centre optimal est situé au noeud b. En considérant une partition

en deux ensembles, le centre optimal est cette fois situé au noeud a puisque que sa partition a

une pondération plus élevée en nombre de villes (9 villes):

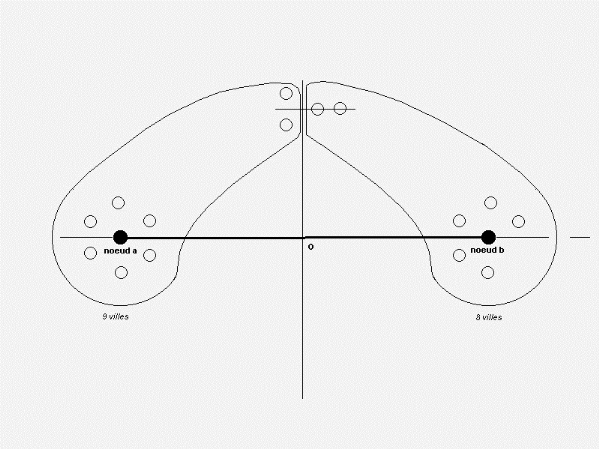
Fig. 2.20 - Partition des 17 villes en 2 ensembles

De plus, on peut se poser la question de savoir si certaines villes, ou paquets de villes, très éloignées valent ou non la peine d'être prises en compte dans l'étude de localisation: quel que soit leur potentiel de clientèle même faible, leur éloignement a tendance à attirer vers elles le (ou les) site(s) à implanter sans que cela ne vaille peut-être la peine. Dans l'exemple précédent, la partition constituée des quatre villes du noeud c est d'une importance moindre devant les deux autres partitions des noeuds a (7 villes) et b (6 villes). Si le problème était de livrer un produit ou un service à partir du noeud a à un ensemble de clients, faudrait-il intégrer

les clients associés au noeud c qui, compte tenu du faible potentiel et du coût de déplacement, engendrerait une faible rentabilité ? La réponse à cette question n'est pas fournie par l'analyse typologique et ses méthodes de partition qui traitent le problème d'une manière brute et mathématique.

Outre le fait de fournir des résultats rationnels, le développement de méthodes plus

performantes dans la recherche de localisations optimales doit conduire à notre sens, à

améliorer la capacité du p-médian à traiter des réseaux de plus en plus importants afin de modéliser de manière plus précise le monde réel et pouvoir prendre en compte par exemple l'ensemble des clients d'une grande surface, le réseau Internet et ses nombreux ordinateurs, la

totalité des entrepôts d'un transporteur,...

Conclusion

Ainsi, les théories de la localisation rassemblent un certain nombre de modèles dont certains comme le modèle de Christaller ou la loi de Hotelling, deviennent plutôt des curiosités intellectuelles en présentant la réalité sous un jour très idéal, mais permettent néanmoins de prendre conscience des phénomènes non-aléatoires de répartition des activités commerciales dans l'espace. D'autres modèles dérivant de la loi de Reilly comme les modèles MCI ou MNL

ont permis d'analyser les variations de fréquentation selon les caractéristiques de l'environnement ou du point de vente considéré. Leur mise en oeuvre pour répondre aux problématiques de localisation reste cependant ardue d'une part par le fait qu'il faille identifier précisément quels sont les paramètres fondamentaux jouant sur le choix des consommateurs

de tel ou tel magasin en se fondant sur l'expérience, et d'autre part, car il est nécessaire de rassembler les données relatives à ces paramètres avant de lancer l'analyse : rien ne prouve d'un autre côté que les paramètres identifiés dans une zone soient transposables dans celle où l'on recherche un ou plusieurs emplacements commerciaux. Les modèles de localisation multiple comme le modèle p-médian jouent essentiellement sur la notion de distance en choisissant les sites les plus proches d'une clientèle potentielle. D'autres variables comme le coût d'ouverture des points de vente, les coûts de déplacement ou même une mesure de

l'attractivité des points de vente avec le modèle Multiloc⁵⁵⁵, peuvent être pris en compte dans

ces modèles ce qui est susceptible de les rendre assez intéressants pour la recherche de localisations multiples optimales. Mais, les algorithmes approchés permettant de résoudre ces problèmes élaborés, trop lents, ne sont pas suffisamment performants pour être utilisés tels quels. Partant d'une base de données de clients potentiels, le processus initial de modélisation conduisant à un réseau de localisation-allocation s'avère souvent être une tâche difficile.

⁵⁵⁵ ACHABAL D.D., GORR W.L. et MAHAJAN V. (1982) Multiloc : A Multiple Store Location Decision

Model, Journal of Retailing, 58.

Alliés au modèle le plus adapté à la localisation multiple de points de vente c'est-à-dire le modèle p-médian, les principes du traitement du signal introduits dans le chapitre suivant réussiront à surmonter ces difficultés en facilitant considérablement à la fois la modélisation d'un réseau de localisation-allocation et la résolution de ce modèle. D'autres avantages

complémentaires apparaîtront à la lecture de l'exposé.