Chapitre 3
L'apport du traitement du signal dans le modèle
p-médian
Introduction
Comme nous l'avons vu au chapitre précédent, la
problématique de recherche de localisations optimales mérite
d'être repensée à la fois sur le plan de la
modélisation et au niveau de la résolution ultérieure
du modèle. Pour cela, il nous est apparu comme pratiquement
logique que les informations concernant la clientèle potentielle des
futurs points de vente devaient être réagencées et si
nécessaire "pré-digérées" au lieu de se
lancer à corps perdu dans la construction d'un modèle
trop complexe à résoudre. Ce pré-traitement peut
être réalisé en faisant appel à une technique de
traitement de l'information assez élaborée et
dénommée dans
le jargon scientifique «traitement du
signal». Le traitement du signal est un domaine d'importance
si l'on s'en réfère aux 50 000 ingénieurs
travaillant sur ce sujet directement à travers le monde et
plusieurs centaines de milliers indirectement. Cette science bien
qu'inconnue il y a cinquante ans, s'est discrètement introduite
dans notre vie quotidienne à travers l'électronique,
l'informatique ou les télécommunications. On pourrait
qualifier le traitement du signal de technique capable de
réaliser des opérations variées sur une
information quantifiable dont la valeur est mesurable sur une certaine
période. Ces opérations peuvent être une simple conversion
(par exemple entre informations analogiques et digitales), une compression de
l'information pour minimiser le nombre de données qui la
caractérise, une correction d'erreur, une amplification destinée
à accroître l'amplitude de cette information,...
Or, malgré la richesse de la recherche en traitement du
signal, sa contribution aux sciences de gestion et en particulier au
géomarketing s'avère pour l'instant très mince. Nous
verrons au cours de ce chapitre que le traitement du signal se combine pourtant
très harmonieusement aux modèles de localisation-allocation
en particulier au modèle p-médian pour faciliter la
recherche de localisations multiples.
3.1 Une nouvelle approche du p-MP par le traitement du
signal : premier aperçu d'un nouvel algorithme rapide de
multilocalisation d'activités
Nous avons abordé le problème de recherche
de localisations optimales par une approche modélisatrice.
L'approche modélisatrice passe par une attention portée à
ce qui est représenté, mais aussi à la symbolisation de ce
qui est représenté, donc aux fondements et aux
propriétés même de la projection556. "Le
système de modélisation est récursif,
s'établissant dans l'interaction entre le système
modélisé (le phénomène perçu comme complexe)
et le système modélisant. [...] Le système de
modélisation (le modélisateur concevant et
interprétant le modèle d'un système complexe) se comprend
comme s'auto-finalisant : il élabore ses projets,
il est projectif "557. Ainsi, le premier
niveau de notre réflexion est global et peut nous conduire
à retenir une méthodologie. Ensuite, les
idées vont se transformer en variables au niveau du système,
"cet ensemble d'unités en interrelations
mutuelles558" qui seront alors analysées et
organisées pour parvenir à des conclusions en effectuant
un retour vers le niveau initial (processus récursif).
Ceci nous a conduit à élaborer un algorithme du
type poupées russes. Son organigramme sera d'ores et déjà
présenté étant donné que certaines de ses
fonctionnalités, comme la délimitation
de zones de chalandise, mériterons d'être
améliorées vis-à-vis de l'état de l'art
existant (cf. chapitre II). La modélisation des données a
été faite par une analyse systémique de la zone de
chalandise composée de la demande 'les clients). Il s'agit de
définir un modèle de données de
la zone de chalandise composée d'objets
c'est-à-dire les aires de la zone de chalandise denses
en clientèle (voir pages suivantes). Cette approche
correspond à l'idée de modélisation
556 MABILLOT V. (2000) Mises en Scène
de l'Interactivité : Représentations des Utilisateurs dans
les
Dispositifs de Médiations Interactives, Thèse
soutenue le 7 janvier 2000, Université de Lyon II, p.6
557 LE MOIGNE J.L. (1990) La modélisation
des Systèmes Complexes, Bordas, Paris, 178p.
558 VON BERTALANFFY L. (1968) Théorie
générale des systèmes, Trad. fr. par J. B. Chabrol.,
Dunod, Paris.
projective avancée par Le Moigne où le
territoire géographique est analysée à
différentes échelles 559.
Rappelons et résumons tout d'abord à nouveau la
problématique à résoudre.
Problématique:
Trouver les localisations optimales pour un ensemble de p
activités destinées chacune à servir
un ensemble de clients, de telle manière que la somme
totale des distances de l'ensemble des activités à ses clients
soit minimale, avec la contrainte que le nombre n de clients est
élevé. Les données disponibles sont au minimum la
localisation spatiale des clients représentée par exemple par
leurs adresses, le nombre p d'activités à localiser et
éventuellement le niveau de demande de chaque client quant aux services
ou aux produits offerts par lesdites activités.
L'algorithme recherchera une solution globale avant de
s'attaquer à la recherche d'une solution locale ce qui permettra de
simplifier le problème. Voici l'organigramme de l'algorithme
proposé :
559 CRAUSAZ P.A., MUSY A., MATTEI A. (1999) GESREAU :
GESREAU: Ein Konzept für ein Integriertes
Management der Fliessgewässer, Rapport de l'Hydram, Suisse,
p.6
Nous proposons dans ce cadre l'algorithme global suivant qui
prendra en compte les données
disponibles pour les traiter dans l'optique de résoudre la
problématique exposée :
Initialisation:
Echelle Globale
Géocodage: Repérer
les
1 clients à l'aide de leurs
coordonnées spatiales.
Délimitation: Délimiter des
zones homogènes de
2 localisation de clients à
l'aide de filtres et/ou d'un
algorithme morphologique.
Identification des centres
3 de gravité: les centres de
gravité constitueront les
noeuds d'un réseau.
Changement d'échelle: Echelle plus fin e,
locale
Résolution du p-MP: les
4 algorithmes du p-médian sont
utilisés pour trouver les
p localisations d'activités.
La résolution est-
elle suffisante ?
Non
Oui
Fin
Fig. 3.1 - Organigramme du nouvel algorithme proposé
Explicitons le fonctionnement de cet algorithme
avant d'étudier plus précisément ses
différentes fonctions: notre procédure de recherche de
localisations optimales comprend donc quatre phases suivies d'une boucle de
rétroaction. Elle fonctionne en quelque sorte par effet
loupe en s'attachant dans un premier temps à
déterminer les meilleurs emplacements au niveau global, par exemple
au niveau national, puis à faire une boucle pour réitérer
le même processus mais au niveau local. Les noeuds du
modèle p-médian sont constitués dans un premier temps
des zones géographiques (zones de chalandise) dans lesquelles la
densité de clients est homogène et plus importante qu'ailleurs.
Les frontières de ces zones de chalandise seront
déterminées, comme nous le verrons plus loin, par les
méthodes classiques utilisées en traitement du signal qui
rassemble en fait un ensemble d'outils mathématiques
destinés à extraire de manière rapide des informations
précises d'une source.
Dans un second temps, on se concentrera sur les p
noeuds calculés par l'algorithme de résolution et on
déterminera au sein de chacun de ces p zones géographiques
à nouveau un certain nombre de noeuds constitués de la
même manière de zones de clientèle homogènes
mais au niveau local cette fois. Le modèle p-médian (ou
un autre modèle incorporant des paramètres de coût, de
concurrence ou des critères socio-économiques) sera
ré-appliqué dans chacune de ces p zones locales de
manière à améliorer la précision de
localisation des activités.
Les dessins suivants résument le fonctionnement de
ce nouvel algorithme fondé sur la délimitation de zones de
chalandise.
1
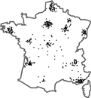
La phase 1 consiste à codifier les
adresses de clients potentiels ou réels
en termes de coordonnées géographiques, adresses
tirées d'une base de données. On pourra alors obtenir une
représentation cartographique des différentes localisations de
la clientèle, chaque client étant représenté
par un point.
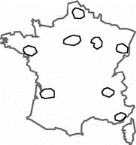
2
La phase 2 correspond à la
délimitation des "paquets" de clients ou aires appartenant
à la zone de chalandise. Nous utiliserons dans cette optique les
techniques de traitement du signal qui font aussi l'originalité
de notre démarche.
3
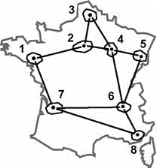
On calculera dans la phase 3 les
coordonnées des centres de gravité
de chaque aire délimitée dans la phase
précédente de manière à modéliser un
réseau: les noeuds du réseau seront représentés par
les centres de gravité et les segments par les distances
routières ou par un indicateur d'éloignement (temporel,
kilométrique, généralisé...). Des localisations
potentielles supplémentaires pourront d'autre part être
introduites comme noeud même si elles ne comptent pas de
clients. Ce réseau peut être, si nécessaire,
pondéré et dans ce cas, à chaque noeud sera
affecté un poids représentatif de l'importance de
la clientèle ou de son potentiel.
4
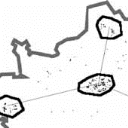
Dans la phase 4, le réseau sera
résolu sur la base du modèle p-médian grâce aux
algorithmes classiques de résolution et d'amélioration. On
aboutira donc au choix de certains noeuds comme localisations
optimales.
Rétroaction et changement d'échelle:
après avoir identifié les p noeuds optimaux par
l'algorithme du p-médian, on pourra, si un degré de
précision supplémentaire s'avère nécessaire,
réitérer le processus en se concentrant cette fois au niveau de
chaque noeud. L'examen d'aires de plus en plus petites pour améliorer la
finesse du choix de localisation pourra se faire autant de fois que
souhaité sous réserve de l'existence d'un nombre suffisant
de clients ou d'emplacements potentiels à cette échelle.
Ainsi, la partie centrale et novatrice de cette méthode
est constituée par la délimitation des
aires de chalandise (zones denses de clientèle appartenant
à la zone de chalandise) au niveau
desquelles il sera possible de définir un centre de
gravité caractérisant la localisation spatiale
de ladite aire. Ces centres de gravité
constitueront les noeuds d'un modèle p-médian. Il est donc
fondamental de définir avec précision les contours de
ces aires de chalandise: une évaluation grossière des
frontières induira nécessairement un repérage des centres
de gravité entachés d'erreurs ce qui ne manquera pas de se
répercuter sur le résultat final de localisation des p centres au
niveau global et plus encore au niveau local. La deuxième innovation
découle
du fait que l'on simplifie le problème en
l'appréhendant de manière globale grâce à
l'identification de "paquets" de clients, et qu'ensuite seulement, on
pousse l'analyse dans le détail en recherchant dans les zones
intéressantes des emplacements plus précis toujours en utilisant
la délimitation d'aires de chalandise caractérisées
par leurs centres de gravité et le modèle p-médian.
Cette technique utilise à la fois des principes de la localisation
discrète (à travers le modèle p-médian) et
celles du modèle planaire (à travers le calcul de
centres de gravité).
Le prochain paragraphe donnera tout d'abord
l'occasion de récapituler les techniques existantes de
traitement du signal, puis de montrer leur capacité à
s'intégrer dans une problématique de multilocalisation
d'activités du type p-médian.
| 


