3.2 Méthodes de délimitation fondées
sur le traitement du signal et l'analyse d'image
La première étape de l'algorithme introduit
précédemment et destiné à localiser un ensemble
de points de vente avec un bon niveau
d'optimalité consiste à délimiter les zones de
chalandise. Or, comme on l'a vu au chapitre 1, les méthodes
actuelles de délimitations comportent un grand nombre de lacunes et
d'imprécisions.
3.2.1 Introduction au traitement du signal et à
l'analyse d'image
Les limitations précédentes se devaient
d'être surmontées en introduisant une nouvelle approche pour
délimiter les aires composant la zone de chalandise ou même toute
autre zone géographique possédant des
caractéristiques commerciales, économiques, sociologiques
propres. Cette nouvelle solution devait à la fois être rapide,
précise et pouvoir être convertie
en algorithmes de manière à pouvoir être mise
en application sur ordinateur et de préférence sur les
calculateurs les plus courants du marché, c'est-à-dire les
micro-ordinateurs.
Pour répondre à ces exigences, il est un
fait que les algorithmes nécessitant la plus grande vitesse
d'exécution sont ceux fonctionnant en dynamique. Dans ce cas, les
informations issues
de capteurs sont fournies en temps réel au calculateur
qui les traite au même rythme que les données sont
prélevées. Outre les applications purement
électroniques, les domaines qui utilisent ce genre de
traitement d'information ne sont pas légion et se
rassemblent essentiellement autour du traitement du signal. Le traitement du
signal vise à interpréter une information possédant une
certaine continuité soit dans le temps, soit dans l'espace. Il s'agit
ainsi d'arriver à distinguer, dans la masse de données, les
informations non-aléatoires, et de caractériser ces
données atypiques pour éventuellement les reconnaître
à chaque fois qu'elles
se présenteront à nouveau. De nombreuses
applications utilisent les principes du traitement du signal dont la plus
élaborée est la vision artificielle, une technique
complémentaire de la robotique. D'autres disciplines font largement
appel au traitement du signal comme toutes les sciences désireuses de
rendre de façon automatique le résultat de leurs observations.
Ainsi,
ont procédé la cristallographie et la
biologie en microscopie électronique, la médecine en
échographie et radiographie, la géographie et la géologie
pour traiter les images prises d'avion
ou de satellite, l'acoustique pour les signaux sonores, la
climatologie dans l'interprétation des
images radars, la physique pour l'examen des spectrographes,
etc... Les premières études sur
la vision artificielle furent menées à
partir de 1950 par Gibson 560 à Boston puis dans
les années 60 dans le domaine de la recherche spatiale en particulier
pour tout ce qui concerne le traitement des images provenant des sondes et des
satellites. Plus tard, la robotique, avec les travaux de Binford 561
et de Horn 562 563, a pris le relais dans le
développement de ce domaine récent qui allait désormais
s'appeler visionique ou computer vision en anglais.
On observe une grande similitude entre les
données issues de capteurs électroniques ou optiques et les
données géomarketing. Ces données, quelle qu'en soit la
source, sont en effet variables dans l'espace et dans le temps. D'autre part,
les capteurs ou les moyens d'obtention des informations marketing
n'étant pas parfaits, elles comportent toutes des erreurs de mesure soit
aléatoires du type neige, soit de type absences d'information,
soit encore de type perturbations hautes ou basses fréquences
liées à des interférences dans le cas de capteurs
"physiques" ou liées au mode de collecte des données dans le cas
de données géomarketing.
McKay 564, de l'Université d'Indiana, fut le
premier à avoir noté que les données
géomarketing
comportaient un signal de base avec une perturbation,
le bruit, à éliminer par un filtrage approprié. Son
travail s'est malheureusement limité à un filtre médian de
base sans explorer toutes les possibilités qu'offre la science du
signal.
Il y a quatre étapes fondamentales qui se succèdent
d'une façon générale dans le processus d'analyse du signal
et qui sont dans l'ordre:
%o l'acquisition des données par un
capteur, dans le cas du géomarketing, ce capteur prenant la forme
d'une enquête auprès d'une population donnée de clients
effectifs, de
clients potentiels, de non-clients ou de toutes autres
informations commerciales
560 GIBSON J.J. (1950) The Perception of the
Visual World, Editions Houghton-Miffin, Mass., Boston.
561 BINFORD T. (1971) Visual Perception by Computer,
IEEE Systems Science & Cybernetics Conference, FA, Miami.
562 HORN B.K.P. (1975) The Psychology of Computer
Vision, Editeur P.Winston, NY.
563 HORN B.K.P. (1986) Robot Vision,
Editions MIT, Press Mc Graw-Hill, NY.
564 MCKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
quantifiées et liées à une
localisation géographique précise. Dans le cas de
données d'adresses, celles-ci sont géocodées afin
d'obtenir une cartographie représentant l'ensemble des clients
potentiels.
%o le pré-traitement des données
destiné à éliminer les imperfections du capteur
ou de
la source d'information à savoir dans le cas d'une
enquête marketing, les non-réponses
ou l'absence de réponse, les fausses
réponses, les erreurs d'échantillonnage ou les biais,
%o le traitement à proprement parler
qui s'attache dans notre problématique à détecter
par des algorithmes les frontières de la zone de chalandise,
%o l'exploitation des résultats qui
vise à caractériser les informations extraites de la
masse des données, ici, en l'occurrence, il s'agit de donner les
caractères propres à la zone de chalandise,
c'est-à-dire les paramètres géométriques qui
vont nous servir à construire le modèle p-médian tels
que les coordonnées des centres de gravité (noeuds
du réseau) de chaque aire composant la zone de
chalandise ou éventuellement la surface de ces aires (qui pourra
constituer une possibilité de mesure de la demande).
Nous allons maintenant décrire plus
précisément les étapes de pré-traitement
et de délimitation des zones de chalandise sachant que nous supposons
avoir obtenu à ce stade une cartographie des données d'adresses
clients. Les deux étapes suivantes seront illustrées par des
exemples concrets de délimitation de zones de chalandise
théoriques. A noter que la répartition de clients dans
l'espace va être prise en considération à titre d'exemple,
mais on aurait aussi bien pu, en suivant les mêmes
méthodes, s'attacher à la délimitation de zones
d'implantation de commerces ou d'activités de services.
3.2 2 Le géocodage et la représentation des
données géomarketing
La première phase de notre algorithme consiste donc
à repérer les coordonnées géographiques des
clients: leur localisation conditionnera en effet le choix
d'une (ou de plusieurs) localisation(s) d'activités. Supposons
qu'on connaisse la localisation géographique de la
clientèle d'un point de vente. Une base de données
d'adresses peut être construite grâce à l'information
obtenue à partir:
1- des cartes de fidélité (grands magasins,
chaînes) 
2- des modes de paiement comme les chèques (magasins,
banques)

3- des bulletins d'un jeu-concours spécialement
organisé pour l'occasion 

4- d'un repérage des immatriculations des véhicules
sur le parking
s)
5- d'une enquête directe (questionnaire auprès des
client

.
En utilisant en premier lieu, la méthode empirique, on
représente chaque adresse client par un
point sur un graphique correspondant au plan
géographique 2D (géocodage), on obtient un nuage de points
dont la densité varie dans le plan en fonction de la
concentration de la clientèle. Les amas de points figurent les zones
de chalandise à partir desquelles le point de vente tire l'essentiel de
sa clientèle. L'oeil humain réussit assez bien, en visualisant
une telle carte, à délimiter les frontières de ces
amas grâce à ses fonctions performantes d'analyse spectrale.
Ceci dit, la vision humaine n'est pas parfaite et un examen visuel, outre le
fait que
ce mode de procédure, pour délimiter les zones de
chalandise, est long et fastidieux, risque de
conduire à des erreurs d'interprétation.
La délimitation analytique des aires denses
s'avère aussi difficile sur le plan mathématique mais
nécessaire néanmoins si l'on veut non seulement bien
connaître sa clientèle, par exemple pour de futures
opérations promotionnelles (mailing par quartier), mais aussi pour
s'assurer de
la bonne localisation de ses points de vente.

Y
O X
Fig. 3.2 - Exemple de représentation de clients sous forme
de pixels
Si l'on revient au cas précédent,
l'analyse peut porter sur les données d'adresses clients
précédemment évoquées ou bien encore sur les
données de fréquentation du point de vente. A chacun des k
clients C1,...Ck , recensés, on peut associer une fréquentation
du point de vente respectivement f1,...,fk sur une période T qui est
choisie de manière adéquate (une semaine, un mois, un an,...)
selon le type de point de vente considéré.
Les données d'enquête sont de type discret tout
comme les données graphiques numériques,
ce qui facilite leur représentation visuelle (Le
présent exposé mathématique pourrait être
établi sans mise en parallèle avec une quelconque
représentation visuelle, mais cette approche
en facilite la compréhension).
Chaque adresse d'un client Ci correspond à un point
allumé soit un pixel noir de coordonnées
(xi, yi) dans une base orthonormée (OX,OY) : i
variant de 1 à n et j de 1 à m pour un
découpage de la région géographique analysée en n x
m petites zones (xi,yi). Le pixel noir (présence d'au moins un
client) ou blanc (absence de client) correspond dans ce cas à
un élément de l'espace géographique quadrillé sous
forme d'un réseau carré. Ceci dit, le réseau carré
(matriciel), bien que très pratique, n'est pas forcément la
partition la plus adéquate de l'espace géographique, car celle-ci
ne conserve pas les propriétés topologiques du monde
réel,
et en particulier la propriété de connexité
(contrairement au réseau hexagonal).
Pour améliorer la représentativité de
la zone de chalandise, on peut faire correspondre à chaque
pixel un niveau linéaire de gris (ou de couleur) en fonction soit du
nombre de clients dans la zone (xi,yi), soit de la somme f = fij
des fréquentations du point de vente par l'ensemble des clients de
la zone (xi,yi) sur une période T. Ce codage est souhaitable lorsque
le quadrillage de la zone géographique possède une
faible résolution (peu de pixels). D'autres
variables peuvent être bien sûr prises en compte
selon les préoccupations de l'analyse, comme
le chiffre d'affaires (ou la rentabilité)
lié à chaque client sur une période de temps. Si
l'on considère par exemple chaque pixel d'une matrice carrée 512
x 512, formé d'une information codée sur 8 bits, on a alors
256 niveaux de valeurs disponibles pour chaque point pour un
encombrement mémoire sur 256 k octets. Le dessin suivant montre
une possibilité de représentation des points-clients sur une
carte bidimensionnelle.
Y
O  X
X
Fig. 3.3 - Exemple de localisation de clients associés
à leur fréquentation, sous forme d'un nuage de pixels en niveaux
de gris
Il existe cependant de nombreuses possibilités
différentes de représentations graphiques des
données géomarketing que par des points comme :
%o la projection cavalière qui est une
représentation en 3 dimensions des données
géomarketing (exemple: niveau de fréquentation des clients d'un
magasin) dans l'espace géographique:

Fig. 3.4 - Exemple de projection cavalière
%o les lignes de Niveau délimitant les
frontières de zones possédant des valeurs homogènes
(exemple: niveaux d'équi-fréquentation):
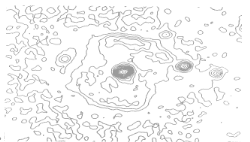
Fig. 3.5 - Exemple de lignes de niveaux
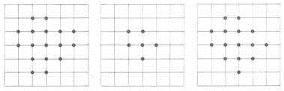
%o le code Ternaire qui est une simplification de
la représentation ponctuelle. Ce code de représentation ne
possède que 3 valeurs possibles avec par exemple, si l'on
considère les différents types de zones d'une ville en termes de
fréquentations d'un point de vente, les zones comptant au moins un
client (point foncé), les zones comptant uniquement des
habitants non-clients (point clair) et les zones urbaines sans
habitants (en blanc):

Fig. 3.6 - Exemple de représentation en code ternaire
Après avoir vu les modes de représentation
possible des données géomarketing et la manière d'obtenir
les adresses, l'étape suivante consiste à délimiter les
aires denses en terme de clients dont le regroupement est appelé
communément "zone de chalandise" (la zone concentrant au mieux le
meilleur du potentiel commercial). Après avoir rappelé les
différentes approches de
ces aires dans la littérature, nous nous proposons
d'introduire de nouvelles méthodes de délimitation pour
pallier le manque de précision et de rapidité des méthodes
actuelles.
3.2.3 Le prétraitement des données par
filtrage
Le prétraitement des données d'enquête
est destiné à faciliter l'analyse des données sans
réduire la qualité de l'information disponible, bien au
contraire. En traitement du signal, la principale méthode
consiste en un filtrage ondulatoire (une image ou une enquête
sur un secteur géographique étant une onde bidimensionnelle). On
cherchera ainsi non seulement à accentuer le crénelage
(accentuation des contours entre les zones de différentes
caractéristiques à peu près homogènes), mais
aussi à s'affranchir de la pollution par des données
atypiques (bruit) dues par exemple à des erreurs
d'enquête (ex. mauvaise administration ou saisie), aux fausses
réponses (ex. fausse adresse) ou tout simplement à des
réponses marginales au sein de la zone de caractéristiques
homogènes.
Comme on l'a déjà vu, McKay est le premier à
avoir utilisé la technique du filtrage sur des
données de localisation spatiale d'un
échantillon de clients 565 en constatant que ces
informations étaient composées d'un signal fondamental de base et
d'un signal perturbateur ou bruit dont il fallait s'affranchir. Mais, cette
imperfection des données n'était pour lui que le fait
de fortes différences comportementales entre des
consommateurs habitant à proximité les uns des autres, alors
que le bruit trouve aussi son origine dans des informations
erronées ou manquantes. Etudiant un échantillon d'une
centaine de clients seulement, le traitement des données
s'était limité à l'utilisation d'un filtre binomial
(filtrage en moyenne pondérée) du
type:
1 / 16
C = [cmn]= 2 / 16
1 / 16
2 / 16
4 / 16
2 / 16
1 / 16
2 / 16
1 / 16
avec, si Zij représente la valeur
mesurée au point de localisation (Xi, Yi), une
nouvelle valeur
Wij modifiée par ce filtre est donnée par :
M N
W ij
=
m = -M n = -N
cmn Z i + m,
j + n
le filtre ayant pour dimension 2M+1 par 2N+1 (c'est-à-dire
M= et N =1 pour le filtre binomial
précédent). Comme on va le voir, le filtre binomial
bien qu'éliminant le bruit lié par exemple à des erreurs
d'enquête n'est pas le plus recommandé pour conserver les
contours.
Le filtrage spatial repose d'une manière
générale sur des opérations ponctuelles appliquées
de manière itérative sur chaque valeur ou agrégat de
valeurs d'une matrice ou d'une image (en quelque sorte des opérations
portant sur les aires géographiques regroupant des clients d'un niveau
moyen de fréquentation homogène). Les filtres spatiaux les plus
courants sont:
565 McKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
- le filtre en moyenne
- le filtre médian
- le filtre sigma
- le filtre Nagao
Il est également intéressant d'utiliser la
transformation de dilatation lorsque les points
représentant les clients sont assez éloignés les uns des
autres et qu'il n'y alors pas possibilité
de distinguer de forme claire de la zone de chalandise.
Le filtre en moyenne
Ce traitement revient à traiter la matrice de
données en prenant comme nouvelle valeur de chaque point, la
moyenne du point considéré aggloméré avec ses
voisins. Il correspond en fait
au filtre binomial avec des coefficients de pondération
égaux à 1. Dans une matrice, chaque élément
(excepté sur les bords) compte 8 voisins adjacents de
même que sur une image à matrice carrée.

Fig. 3.7- 8 voisins adjacents à un point central
Ainsi, la nouvelle valeur f 'i,j de fi,j est :
f 'i,j = [fi,j + fi+1,j+1
+ fi+1,j + fi,j+1 + fi-1,j-1 +
fi-1,j + fi,j-1 + fi+1,j-1 +
fi-1,j+1] / 9
Ce procédé comme tous les filtres binomiaux en
général a l'inconvénient de lisser les données mais
lisse aussi les transitions (les bords d'objets à fort gradient
d'intensité deviennent souvent
flous). Très simple, rapide, il n'est à utiliser
que lorsque la densité des clients dans les aires de chalandise est
faible afin d'obtenir un effet de lissage fort.
le filtre médian
Le filtrage en moyenne compte tenu de ses inconvénients
peut être avantageusement remplacé
par le filtrage médian, un filtre passe-bas qui a tendance
à accentuer les intensités sans lisser
les bords. La médiane M d'une variable x vérifie
par définition les probabilités suivantes: P(x M) 1/2 et P(M
x) 1/2
Le filtrage médian élimine le bruit de type neige
(erreur dispersée de façon aléatoire) mais au
détriment d'une légère perte de
résolution.
L'exemple suivant représente la même
représentation des localisations de clients virtuels selon leurs niveaux
de fréquentation d'un point de vente (les points foncés
représentent les clients fréquentant assidûment le
magasin, les points plus clairs les clients moins fidèles). Le dessin
à côté montre cette cartographie
traitée par deux filtres médians successifs: les aires de
chalandise à forte fréquentation de clients apparaissent plus
nettement (zones foncées) ce qui facilitera la délimitation des
frontières :
Fig. 3.8 - Adresses clients associées aux
fréquentations Fig. 3.9 - La représentation traitée par 2
filtres médians
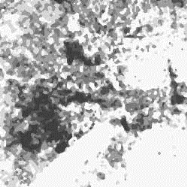

Comme vu précédemment (§ 1.4), nous
remarquons que les zones denses de clientèle ne
forment pas un ensemble géographique compact
566, mais se répartissent en différentes aires
de chalandise (nous dirons que la zone de chalandise se compose
en fait de plusieurs aires de chalandise).
le filtre sigma
Le filtre sigma est surtout un filtre de débruitage. A
tout point (i, j) de la zone image active de niveau de fi,j est
affectée la moyenne de ses voisins dont le niveau appartient
à l'intervalle centré en fi,j de demi-largeur 2 sigma,
sigma étant la variance locale dans la fenêtre.
Toutefois, si le nombre de voisins appartenant à cet intervalle est
inférieur ou égal au nombre
de voisins V=2L+1, alors f i,j sera remplacé par la
moyenne de ses huit voisins immédiats.
Ce traitement est bien adapté au filtrage d'un
bruit impulsionnel (erreur très forte, répétée
mais localisée, cas de réponses totalement erronées
mais rares), en choisissant <2 et L=1 (V=2L+1=3, correspondant
à un voisinage 3x3) ce qui peut être le cas si les
données géomarketing présentent des erreurs importantes
mais espacées.
le filtre de Nagao
Un des filtrages spatiaux les plus utilisés et
les plus intéressants de nos jours est celui de Nagao
567. On considère cette fois le voisinage d'un pas
de deux éléments (ou plus généralement de e
éléments) autour du point (i, j) considéré, soit
une sous-matrice de 5 x 5 =
25 éléments. On calcule ensuite pour 9
configurations compactes d'éléments de 3 types
différents (voir dessin suivant), la moyenne et la variance des
valeurs des éléments les
composant.
566 CLIQUET G., FADY A., BASSET G. (2002)
Management de la Distribution, Dunod, Paris.
567 NAGAO M., (1979) Edge Preserving Smoothing,
CGIP, vol. 9, p.394-407.
1 du type (1) + 4 du type (2) + 4 du type (3)
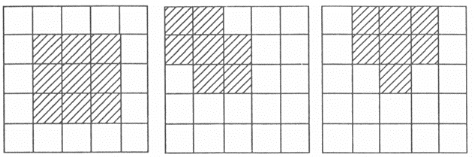
Fig. 3.10 - Les 3 catégories des 9 configurations du
filtrage de Nagao sur lesquelles porte le calcul des moyennes et des
variances
La nouvelle valeur choisie pour le point (i, j) est alors
celle de la moyenne correspondant à la plus faible variance. Ce
traitement est réalisé en considérant tour à tour
tous les points de la matrice des données de fréquentation.
Les contours sont ainsi bien conservés car le
lissage ne se fait que dans sa direction tangentielle
c'est-à-dire dans la direction où la modification est la moins
visible 568. C'est la raison pour laquelle on dit que le filtre de
Nagao est qualifié de lissage avec conservation et même
accentuation des contours. Ce filtrage peut être
réitéré plusieurs fois sur la matrice déjà
traitée. On observe que ce filtre est pratiquement idempotent: au bout
de quelques itérations, l'image (ou la matrice) ne se modifie presque
pas. On arrête alors le processus de traitement. L'exemple suivant montre
la même représentation des localisations de clients virtuels selon
leur niveau de fréquentation d'un point de vente (les points
foncés représentent les clients fréquentant
assidûment le magasin, les points plus clairs les clients moins
fidèles). Le dessin
à côté montre cette cartographie
traitée par deux filtres successifs: on distingue beaucoup plus
nettement les frontières des aires de chalandise à forte
fréquentation de clients (zones foncées
plus homogènes que pour les filtres
précédents):
568 ORSTOM (1998) Image Satellite et Milieux
Terrestre en Régions Arides et Tropicales, Editions de l'Orstom,
Bondy.
Fig. 3.11- Adresses clients associées aux
fréquentations Fig. 3.12 - La représentation traitée par 2
filtres Nagao
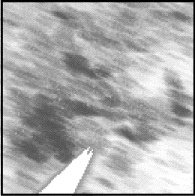

Il existe encore de nombreux autres filtres capables
d'améliorer la qualité de l'image cela afin
de faciliter dans l'étape suivante, le processus
de délimitation des contours des aires. En particulier, de la
même façon que sur une photo de mauvaise
qualité, les données géomarketing sont
susceptibles de comporter soit des perturbations basses
fréquences aléatoires et stationnaires (ex: données
manquantes, échantillon d'enquête trop faible ou base
de données d'adresses clients incomplète) qui
influent négativement sur les frontières de zone
de chalandise en les rendant floues. Un deuxième
type d'interférences est constitué par les perturbations
hautes fréquences liées plus spécifiquement au mode de
collecte des données: il peut par exemple arriver dans une
enquête que tous les 100 questionnaires, il y ait une ou
plusieurs réponses fantaisistes (clients donnant une fausse
adresse ou bien surestimant son taux de fréquentation ou d'achat
dans le magasin). Même si les filtres précédents ont
tendance
à lisser ces erreurs, il existe des filtrages de
fréquence spécifiques dont le rôle est d'assurer la
suppression de ces fréquences non désirées. Le premier
type s'atténue avec les filtres passe- haut (laissant passer les hautes
fréquences) alors que le deuxième s'estompe grâce à
des filtres
passe-bas (laissant passer les faibles fréquences).
La transformation de dilatation
Elle consiste en résumé à grossir les
points représentatifs des clients jusqu'à ce que ceux-ci se
touchent et que l'on distingue les formes pleines de la zone de
chalandise. En effet, dans certains cas, les clients d'un point de vente
représentés sur une carte à la suite d'une phase de
géocodage, apparaissent si éloignés les uns des
autres qu'il est impossible de percevoir les formes de la zone de
chalandise, la dilatation permettant alors de résoudre ce
problème. La dilatation tend donc à connecter les parties
disjointes et à lisser les contours. Nous reviendrons plus
précisément sur cette transformation dite "morphologique"
dans le paragraphe suivant
qui montre comment délimiter de cette manière
les zones de chalandise (la dilatation sera également
utilisée dans la deuxième partie pour lisser les zones de
chalandise constituées par
les clients potentiels de l'Ouest parisien
intéressés par les produits biologiques).
3.2.4 La délimitation des zones de chalandise par
traitement du signal
Après avoir lissé les données par
un filtrage approprié pour obtenir une cartographie plus nette
des données géomarketing, on choisit une méthode parmi
celles disponibles, méthodes toujours inspirées du traitement
du signal ou de l'analyse d'image, pour procéder à la
délimitation de la zone de chalandise. Les méthodes de
délimitation possibles sont:
- une méthode empirique (le seuillage d'histogramme),
- la méthode par masquage et convolution: gradient,
laplacien, Sobel, Prewitt,
- la méthode par analyse morphologique.
· Délimitation par seuillage
d'histogramme
La délimitation par seuillage d'histogramme
consiste en premier à comptabiliser chaque valeur discrète
que les éléments de la matrice f'i,j des fréquentations
préalablement obtenues peut prendre puis de les tracer sous la forme
d'un histogramme. On tente alors de déterminer une valeur seuil T qui
permette de séparer le groupe appartenant à l'objet et celui
appartenant
au fond. Ainsi, pour toute valeur de l'image ou de la matrice
f'i,j supérieure ou égale à T, le point correspondant
appartiendra à la zone de chalandise au contraire des valeurs
inférieures à
T.
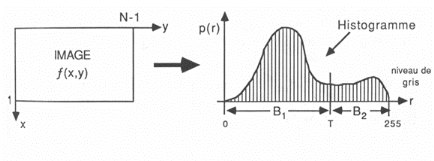
Fig. 3.13 - Exemple de représentation sous forme d'un
histogramme des valeurs f(x,y) des points d'une image
Dans le cas plus général, on peut
réussir à distinguer plusieurs seuils T1,...Ts sur
l'histogramme avec donc plusieurs types de zones de
fréquentation du point de vente considéré par la
clientèle :
si f'i,j < T1, fréquentation quasi nulle
si T1 f'i,j < T2, fréquentation faible
. .
. .
. .
si Ts f'i,j, fréquentation
élevée
Le seuillage T1,...Ts déterminé peut être
soit global (valable pour tout l'espace géographique
analysé), soit local (les valeurs du seuil varie selon les
régions du plan),
Mais, dans beaucoup de cas, l'histogramme ne présente pas
de seuils distinctifs de zones bien nets comme dans l'exemple ci-dessous.
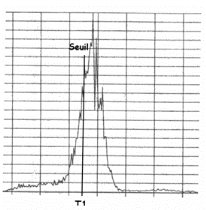
Fig. 3.14 - Détermination d'un seuil de valeurs sur un
histogramme
Une première méthode, empirique, consiste
à tenter de définir un seuil T par tâtonnements successifs
en observant la pertinence de l'image seuillée. Il est
également possible de rechercher un seuil T en considérant que
l'histogramme H(f) est la somme de deux densités de probabilité
:
H(f) = H1 x h1(f) + H2 x h2(f)
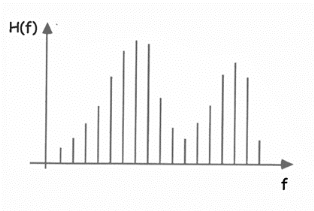
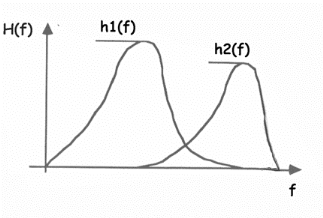
h1(f) et h2(f) sont les fonctions de densité de
probabilité et H1 et H2 sont les probabilités d'existence
de 2 groupes de valeurs dans la matrice (ou des 2 types de niveaux de gris dans
l'image).
Fig. 3.15 - Exemples d'un histogramme et de son enveloppe
comportant plusieurs valeurs de seuils
La probabilité de classement par erreur d'un point
à fréquentation faible dans la zone 2 à forte
fréquentation (zone de chalandise) s'exprime par :
T
E1(T) =
h2(f)df
-
Et inversement, la probabilité de classement par erreur
d'un point à fréquentation importante
(appartenant à la zone de chalandise) dans la zone 1
à faible fréquentation s'exprime par :
+
E2(T) =
h1(f)df
T
La probabilité d'erreur totale est donnée par
: E(T) = H2 E1(T) + H1
E2(T)
Celle-ci doit être minimisée et en
conséquence la dérivée de E(T) par rapport à T est
nulle. On
a donc H1 h1(T) = H2 h2(T). Le seuil T qui permet
de départager les deux densités de
probabilité h1(T) et h2(T) correspond ainsi à
la valeur du minimum de l'histogramme
correspondant à la densité h1(T)
c'est-à-dire :
1 2
P1
T = 2 ( + )+ 1 -2 Ln(P2 )
1 2
1 et 2 étant les luminances
des densités de probabilité p1(f) et
p2(f),
1 et 2 étant les écarts-types de ces mêmes
densités de probabilité.
· Délimitation par le gradient
La méthode par le gradient et celle par le
laplacien décrite dans le paragraphe suivant, utilisent les
différences de valeur entre les points proches pour déterminer
les frontières. Le vecteur gradient qui traduit les variations de
fréquentation des clients dans le sens vertical (composante de
l'abscisse sur la cartographie) et dans le sens horizontal (composante
de l'ordonnée sur la cartographie) a pour expression dans l'espace
f'i,j du chapitre précédent :
f
r i
G =
f
j
f
lim f i, j - f i + h,
j
f lim f i, j - f i, j
+ h
avec
i = h0 h
et j = h0 h
r
La norme du vecteur G orienté dans le sens
de la variation maximale correspond au maximum
de variation d'intensité.
r 2
1/ 2
G = (f )2+ f
i j
en approximation dans les algorithmes, on prend :
r ( f - f
)2 ( f - f
)2 1/ 2
G
i, j
i+1, j +
i, j
i, j+1
et surtout :
r
G f i, j-
f i+1, j + f i,
j- f i, j+1
ou bien lorsque les contours sont peu marqués, on
utilise l'approximation de Roberts
(variations du gradient peu importantes)569 570 :
r
G f i, j-
f i+1, j+1 +
f i+1, j- f
i, j+1
r
Pour délimiter les contours par la méthode du
gradient, il faudra en pratique comparer G à
une valeur seuil T positive. Si
r
G 0 , alors le point considéré appartient
au contour (qui peut
comporter une épaisseur de plusieurs pixels) et dans le
cas inverse, le point appartient au fond
ou à l'objet.
0 0 0
Le gradient s'exprime par l'opérateur matriciel : -1 1
0
0 0 0
· Délimitation par le laplacien
L'opérateur laplacien est défini par :
2f
=
+ 2f
i2
j2
soit en première approximation,
= fi+1, j - 2 fi,j + fi-1,j
+ fi,j+1 - 2fi,j + fi,j-1 =
fi+1,j + fi-1,j + fi,j+1 + fi,j-1
- 4fi,j
On définit la norme du vecteur laplacien par :
2
r
2 1/ 2
= 2f + 2f
i2
j2
569 CANNY J. (1986) A Computational Approach to
Edge Detection, IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-8, No. 6, pp. 679-698.
570 LIM J. S. (1990) Two-Dimensional Signal and
Image Processing, Englewood Cliffs, NJ: Prentice Hall, pp.
478-488.
0 -1
et le laplacien s'exprime par l'opérateur matriciel : -1
4
0 -1
0
-1
0
Le gradient et le laplacien sont en fait des masques
linéaires. Nous examinons dans le
paragraphe suivant la technique de délimitation par
masquage d'une façon générale.
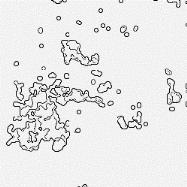
La même représentation des localisations
de clients virtuels selon leurs niveaux de fréquentation
d'un point de vente nous permet d'illustrer le filtre laplacien de
délimitation (dessin de droite) suite à l'application de
deux filtres médians sur la cartographie initiale (dessin de
gauche) conformément à l'étape précédente.
Les contours sont nets mais présentent
des courbes non fermées à ébavurer:
Fig. 3.16 - Adresses clients associées aux Fig. 3.17 - La
représentation traitée par le fréquentations laplacien
après 2 filtres médian

· Délimitation par masquage
Le masquage est un type de filtrage qui généralise
le principe des filtres laplacien et gradient vus précédemment en
faisant appel au produit de convolution de deux fonctions.
Pour rappel, le produit de convolution de deux fonctions f et g :
Z Æ R est une fonction h : Z
Æ R définie par :
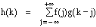
Ses propriétés sont d'être commutatif,
associatif et d'avoir pour élément unité
l'impulsion
unité. On utilise la notation h = f*g. Dans le cas
d'une fonction à 2 variables ou d'une matrice carrée à 2
dimensions telle fi,j (image) convoluée avec une fonction ou une
matrice du même type hi,j , (filtre) on a :
i +k
j +k
gi,j = fi,j * hi,j = f,
hi -, j -
=i -k
= j -k
Fig. 3.18 - L'image fi,j et le filtre
hi,j
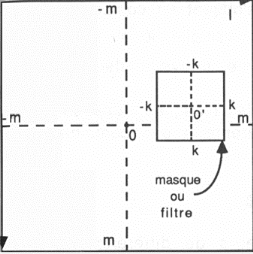
Les dimensions de l'image fi,j et du filtre hi,j sont
respectivement de 2m+1 et de 2k+1 et celle
du produit de convolution de 2(m+k)+1. Si la dimension du filtre
est très petite devant celle
de l'image, ce filtre constitue une fenêtre. Il est
à noter que les bords extérieurs de la nouvelle image issue du
produit de convolution sont entachés d'erreurs.
On a plus spécifiquement pour le produit scalaire
matriciel de 2 matrices A , l'image et M ,
le masque, la notation :
A M
. La matrice résultante
A M
possède les mêmes
dimensions que la matrice image A . Pour une matrice
masque M , 3x3, et le produit scalaire
matriciel est défini par :
3 3
A M
= ai, j mi, j
i = 1 j = 1
avec : 
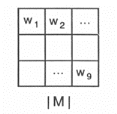
r r
Le produit scalaire Ps s'écrit : Ps =
A. M = a1w1 +
a2w2 + ...+ a9w9
r r
Les coefficients ai et wi
respectivement de A et de M étant rangés dans les vecteurs
A et M .
Le contour s'apprécie en comparant la valeur Ts à
une valeur seuil T. Dans le cas où Ps>T, le pixel transformé
par la convolution est rangé dans la nouvelle matrice de
délimitation.
Voici différents types de masques possibles :
Les masques linéaires
Les masques linéaires les plus connus sont le
gradient et le laplacien déjà évoqués au
paragraphe précédent :
-le Gradient
0 0 0
0 0 0
0 0 0
0 1 0
- 1 1
0 ou
- 1 0
1 ;
0 1
0 ou
0 0 0
0 0 0
0 0 0
0 - 1 0
0 - 1 0
Matrices de détection horizontale ; et matrices de
détection verticale
-Le laplacien
0 0 0
0 0 0
0 0 0
0 1 0
- 1 1
0 ou
- 1 0
1 ;
0 1
0 ou
0 0 0
0 0 0
0 0 0
0 - 1 0
0 - 1 0
Matrices de détection horizontale ; et matrices de
détection verticale
On a en parallèle des masques linéaires pouvant
faire apparaître par convolution uniquement
les frontières d'objet orientés dans une certaine
direction avec par exemple:
- un masque pour la détection des
droites horizontales
- 1
- 1 - 1
2 2 2
- 1
- 1 - 1
- un masque pour la détection des
droites à 45°
- 1 - 1 2
- 1 2
- 1
2 - 1
- 1
Il existe aussi des matrices 3x3 dont les termes sont des
facteurs de corrélation de Markov
(voir chapitre sur le filtre spatial) ou bien des composantes
issues de fonctions gaussiennes. Voici d'autres masques parmi les plus courants
avec dans les masques non-linéaires :
- les masques de Sobel
Ils sont représentés par les deux matrices:
0 0 0
0 1 0
Sx = - 1 1 0
; Sy = 0 0 0
0 0 0
0 - 1 0
Matrice de détection horizontale ; et matrice de
détection verticale
Le "pseudo-gradient" G de Sobel (une approximation du
gradient vu précédemment) est donné par :
G = Gx2 +
Gy
2 1 / 2 ou
G = Gx
+ Gy
(formule encore plus approchée)
avec Gx = (w7 + 2w8 +
w9) - (w1 + 2w2 + w3)
Gy = (w3 + 2w6 + w9) - (w1 + 2w4 + w7)
La direction du pseudo-gradient est alors = tg -1
(Gy / Gx)
Fig. 3.20 - La représentation traitée par
filtres Fig. 3.19- Adresses clients Sobel après 2 filtres médian
(les contours sont associées aux fréquentations superposés
à l'image filtrée par les 2 Nagao)


On remarque que le filtre Sobel possède grâce
à sa fonction de détection des sauts de valeurs
(de fréquentation) la propriété de
fragmenter l'espace à la manière d'un puzzle en séparant
les régions pleines et celles vides de clients. Une suggestion
d'application est que ce filtre pourrait servir à découper de
manière très fine une zone géographique en un certain
nombre
de cellules juxtaposées pour effectuer une
étude sur la proximité spatiale des activités
commerciales ou non, en utilisant le principe de l'analyse quadratique571
572. Cette technique visant à mesurer la dispersion spatiale
des activités repérées par la position du centre
de gravité de ces cellules par rapport à une distribution
aléatoire ou la méthode voisine des plus proches voisins573
ont déjà été utilisées dans de
nombreuses études sur la proximité spatiale
dans des comme le Canada574 575, la
Grande-Bretagne576 577, l'Irlande578 579, la
Suède580, la
571 ROGERS A. (1969) Quadrat Analysis of Urban
Dispersion : 2. case studies of urban retail systems,
Environment and Planning, 1, p. 155-171.
572 BROWN S. (1992) Retail Location : A
Micro-scale Perspective, Ashgate, England.
573 PINDER D.A. & WITHERICK M.E. (1972)
The Principles, Practice and Pitfalls of Nearest-neighbour
Analysis in Linear Situations, Geography, 57,
p.277-288.
574 BOUCHARD D.C. (1973) Location Patterns of
Selected Retail Activities in the Urban Environment : Montreal,
1950-1970, Revue Géographie Montréal, 27, p. 319-327.
575 SMITH S.L.J. (1985) Location Pattern of Urban
Restaurants, Annals of Tourism Research, 12, p. 581-602.
576 SORENSON A.D. (1970) A Comparative
Study of the Changing Patterns of Distribution of Service
Industries on Tyneside, Wearside and Teeside,
unpublished Ph.D. thesis, University of Newcastle-upon-Tyne.
Yougoslavie581, Israël582,
Singapour583, l'Australie584, Hong Kong585 ou
le Japon586. L'analyse quadratique difficile à mettre en
oeuvre, compare donc la distribution des localisations par rapport
à celle qui aurait été générée
aléatoirement : les résultats de cette technique risquée
sont malheureusement sujets à variation en fonction du
découpage géographique retenu de l'aire d'analyse. La
méthode des plus proches voisins consiste, quant à elle, en une
mesure de l'écart d'une configuration spatiale de points par
rapport à une répartition aléatoire : le
problème est que, selon l'étendue de la zone d'analyse,
les mêmes distributions de points peuvent engendrer des mesures
différentes de proximité spatiale et que la méthode est,
d'une manière générale, très sensible aux effets de
bord 587 588 589. La majorité de ces études
ont cependant remarqué que les commerces de détail avaient
tendance à se regrouper comme le prévoit la loi de Hotelling
590 (voir § 2.1.1), au niveau des zones urbaines surtout en ce
qui concerne la distribution de biens élaborés comme les
grands magasins, le prêt-à-porter
féminin, à l'inverse des stations-service ou de
certaines activités de services basiques. Le filtre
577 SIBLEY D. (1975) A Temporal Analysis of the
Distribution of the Distribution of Shops in British Cities, unpublished
Ph.D. thesis, University of Cambridge.
578 PARKER A.J. (1973) The Structure and Distribution
of Grocery Shops in Dublin, Irish Geography, 5, p. 625-
630.
579 BRADY J.E.M. (1977) The Pattern of
Retailing in Central Dublin, unpublished M.A. thesis, University
College Dublin.
580 ARTLE A. (1959) Study in the Structure of the
Stockholm Economy : Towards a Framework for Projecting
Metropolitan Community Development, Business
Research Institute, Stockholm School Economics, Stockholm.
581 ROGERS A. (1974) Statistical Analysis of
Spatial Dispersion, Pion, London.
582 SHACHAR A. (1967) Some Application of
Geo-statistical Methods in Urban Research, Papers of the
Regional Science Association, 18, p.85-92.
583 WING H.C. & LEE S.L. (1980) The
Characteristics and Locational Patterns of Wholesale and Service
Trades in the Central Area of Singapore, Singapore
Journal Geography, 1, p.23-36.
584 JOHNSTON R.J. (1967) Land Use Changes in the
Melbourne CBD : 1857-1972, Troy, P.N., (ed), Urban
Redevelopment in Australia, Research School of Social
Sciences, Urban Research Unit, Australian National
University, Canberra, p. 77-201.
585 LEE Y. (1979) A Nearest-neighbour Spatial
Association Measure for the Analysis of Firm Interdependence,
Environment and Planning A, 1, p. 169-176.
586 OKABE A., ASAMI Y. & MIKI F. (1985)
Statistical Analysis of the Spatial Association of Convenience- good Stores by
Use of a Random Clumping Model, Journal of Regional Science, 25, p.
11-28.
587 PINDER D.A. & WITHERICK M.E. (1972)
The Principles, Practice and Pitfalls of Nearest-neighbour
Analysis in Linear Situations, Geography, 57,
p.277-288.
588 DE VOS (1973) The Use of Nearest-neighbour
Methods, Tijdschrift voor Economische en Sociale Geografie,
64, p. 307-319.
589 RODER W. (1975) A Procedure for Assessing
Point Patterns without Reference to Area or Density,
Professional Geographer, 27, p. 432-440.
590 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, Vol. 39, p 41-57.
Sobel pourrait donc avantageusement servir à construire
de manière précise et harmonieuse le découpage
géographique introduit dans ce type d'études qui deviendrait
ainsi plus fiable (les découpages retenus dans la plupart des cas
étaient les limites administratives pas forcément très
logiques).
D'autres masques sont pratiquement équivalents au
masque Sobel comme les masques de
Kirch ou de Prewitt:
7
- le masque de Kirch
Le pseudo-gradient est cette fois donné par l'expression
:
G = max
1, max[ 5Si - 3Ti ]
i = 0
avec : Si = wi + wi+1 +
wi+2 et Ti = wi+3 + wi+4 +
wi+5 + wi+6 + wi+7
- le masque de Prewitt
Le masque de Prewitt 591 est l'un des filtres du type
dérivatif le plus simple.
- 1 - 1
- 1
- 1
0 1
Px = 0
1
0 0
1 1
; Py = - 1
- 1
0 1
0 1
Détection Horizontale Détection Verticale
Il existe aussi de nombreux masques commerciaux
proposés par diverses sociétés comme
Robotronics, ITMI, Visiomat, FTR proposent d'autres types de
détermination de contour par
le procédé de masquage. Vicom, par exemple
propose l'extracteur de contour (passe-haut)
suivant:
591 PREWITT J.M.S. (1970) Picture Processing and
Psychopictories, Academic Press, p.75.
1 - b 1
( 1 )2 - b b²
- b
b + 2
1
- b 1
suivi par un atténuateur (filtre passe-bas pour supprimer
les aires de clientèle bien identifiées
mais trop petites pour être intéressantes dans
l'analyse):
1 b 1
b
( 1 )2 b² b
b + 2
1 b 1
b pouvant adopter selon les cas une valeur comprise entre 0 et
9.
Voici un algorithme général qui sera capable
de mettre en oeuvre tous ces processus de masquage:
FONCTION MASQUE;
DEBUT
DE i=1 A largeur
DE j=1 A hauteur
DE x=1 A 3
DE y=1 A 3
ImageTransformée(i, j) = ImageTransformée(i, j) +
Masque (x, y) x
ImageOriginale(i+x-1, j+y-1);
FIN FIN
FIN FIN
(les instructions de programmation sont en caractères
gras).
· Délimitation par transformation
morphologique
L'application de la théorie du morphisme
mathématique à la science de la localisation vise à
pallier ces manques en rationalisant le concept de zone de
chalandise. Le morphisme mathématique qui s'inspire de notions de
topologie, de traitement du signal, de probabilités et
de théorie des graphes comporte un grand nombre
d'applications qui toutes relèvent du monde réel. Les domaines
intéressés par cette technique sont très variés et
l'on trouve par exemple la science des matériaux, la géologie, la
biologie, la géographie, la robotique. Le point commun des champs
d'applications possibles est que les données traitées sont
variables dans un espace d'observation assez souvent supérieur ou
égal à deux dimensions.
Le morphisme mathématique s'attache à analyser
les informations dans leur globalité. Voilà pourquoi, cette
science a beaucoup apporté, comme son nom l'indique, à la
reconnaissance des formes (empreinte digitale; voix, écriture;
structure des matériaux; structure géologique, cytologique ou
génétique; circuit électronique) et donc au traitement des
images provenant de diverses sources: enregistrement sonore, photographie,
microscopie électronique ou optique, images satellites, images radar ou
sonar, radiographie, échographie.
Or, pourquoi ne pas utiliser les méthodes du
morphisme, en s'appuyant sur le principe d'universalité des
mathématiques, sur d'autres données que celles acquises
par vision ou enregistrement direct du monde réel ? Le morphisme est
en effet tout aussi apte à traiter des informations qui sont issues
de capteurs humains (ex. enquêtes marketing quantitatives ou
qualitatives) que de capteurs électroniques ou optiques ainsi que de
bases de données mixtes. Cette nouvelle méthode fondée
sur le morphisme mathématique peut être décrite par
une succession de plusieurs étapes:
· Segmentation des données
· Amincissement et régularisation de la
frontière de la zone de chalandise
Segmentation des données
Avant de poursuivre la description du traitement sur la matrice,
nous allons évoquer certaines notions utiles sur les transformations
morphologiques de base.
Transformations Morphologiques de Base: dilatation -
érosion - fermeture - ouverture - chapeau "haut-de-forme"
Les premiers filtres morphologiques sur des données
discrètes ou continues datent de la fin
des années 1970 592 593, mais c'est entre 1982
et 1986 que les Français Matheron et Serra ont établi une
théorie de la morphologie mathématique possédant une
véritable unité 594 595.
Voici les principes fondamentaux de cette théorie
d'analyse des formes :
Soit X un ensemble connexe de données binaires d'une
matrice (0 ou 1, point allumé ou éteint dans un espace 2D),
une première transformation de base possible de cet ensemble
est la dilatation binaire 596 qui a pour effet d'augmenter
la surface totale de cet ensemble. Elle tend à
connecter les parties disjointes et à lisser les
contours.
592 MEYER F. (1978) IIème Symposium
Européen d'Analyse d'Images en Sciences des Matériaux, Biologie
et
Médecine, 4-7 oct. 1977. Pract. Met., S8, p. 374,
Caen, France.
593 STERNBERG (1979) Proc. 3rd Int. IEEE
Comprac, Chicago 1979.
594 SERRA J. (1982) Image Analysis and
Mathematical Morphology, Academic Press.
595 MATHERON G. (1982) Les Applications
Idempotentes, Rapport du Centre de Géostatistique et
de
Morphologie Mathématique n°743, Ecole des
Mines, Fontainebleau.
596 MINKOWSKI H. (1903) Mathematics Annals,
Vol. 57, p.447.
Fig. 3.21 - Exemple d'une dilatation:

en hachures, la forme originale
Une autre transformation morphologique de base est
l'érosion binaire 597 qui lisse aussi la
surface mais à l'inverse la réduit.
Fig. 3.22- Exemple d'une érosion:
en hachures, la forme originale
Pour obtenir des contours plus réguliers, il est
possible de réaliser une succession d'érosion- dilatation
c'est-à-dire qu'en partant de l'image initiale, on élimine tous
les points de la forme considérée en contact en bas, en
haut, à droite ou à gauche avec au moins un point
n'appartenant pas à la dite forme (érosion). Seule, donc,
restent les points de sa partie intérieure. Puis, on entoure
chaque point frontière de la forme érodée de nouveaux
points, à
597 HADWIGER H. (1957) Vorlesung Über
Inhalt, Oberfläche und Isoperimetrie, Springer Verlag, Berlin.
droite, à gauche, en haut, en bas (dilatation).
Fig. 3.23 - Image Initale, érosion, puis dilatation.
Si on considère au lieu de données binaires, des
données réelles comme les fréquentations fi, j
préalablement définies, alors on a un relief qui
varie en tout point défini par ses coordonnées
(i, j) selon la valeur fi, j , (ensemble de valeurs
représentées par la matrice [ f i, j ]).
La dilatation ou l'érosion binaire peut être
généralisée aux paramètres évoluant sur un
éventail
de données 598 comme les
fréquentations fi, j : dans la transformation d'érosion, la
valeur de chaque point est remplacée par la valeur la plus
basse l'entourant à moins qu'elle n'ait la valeur la plus
élevée parmi tous ses voisins. La dilatation est
définie de la même manière, suivant le principe
qu'une dilatation d'une forme est l'érosion de son
complémentaire. Appliquée à de telles données, la
dilatation a tendance à élargir les vallées et à
abaisser les pics.
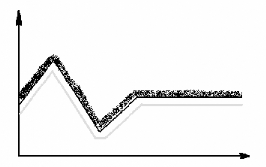
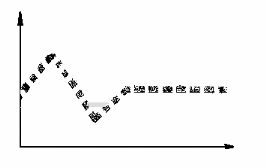
Fig. 3.24 - En Noir: La Courbe Originale / En Gris: a courbe
transformée par dilatation

598 CHERMANT J.L. et COSTER M. (1989)
Précis d'Analyse d'Images, Presses du CNRS.
Fig. 3.25 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par dilatation

Les régions à valeurs maximales ont tendance
à élargir leur surface et les régions à valeurs
minimales décroissent. Dans le cas de l'érosion, les
vallées sont élargies et les pics sont abaissés:
Fig. 3.26 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par érosion
Les régions à valeurs minimales ont tendance
à élargir leur surface et les régions à valeurs
maximales décroissent.
La transformation morphologique de fermeture combine la
dilatation et l'érosion (remplit les
vallées sans transformer les pics).
Fig. 3.27 - En Noir: la courbe originale / En Gris: la courbe
transformée par fermeture
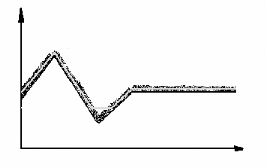
On peut citer aussi la transformation morphologique
d'ouverture qui est la succession, dans
cet ordre, d'une érosion et d'une
dilatation de même taille. Enfin, la transformation
morphologique du "chapeau haut-de-forme" est la soustraction des
données de la matrice initiale [f i, j] aux
données de la matrice fermée [f T i,
j]. Elle constitue un filtre morphologique
qui met donc en évidence les contours. Un exemple
à la fin de ce paragraphe montre son
utilisation pour délimiter les frontières d'une
zone de chalandise.
Fig. 3.28 - En Noir: la courbe originale / En Gris: la courbe
transformée par chapeau haut-de-Forme
La matrice résultat est faite de données binaires
correspondant à une valeur de 1 si l'élément
de matrice appartient à la frontière, et
inversement à une valeur nulle.
· Amincissement et régularisation de la
frontière de la zone de chalandise
Les éléments binaires appartenant à la
frontière de la zone de chalandise sont amincis. Ceci signifie que
pour un ensemble d'éléments caractérisant la
frontière, seul l'élément moyen représentatif de
cette frontière est maintenu dans la matrice tandis que les autres
éléments sont mis à 0.
Les points qui ont été calculés lors de
la dernière étape sont liés par les courbes
régulières de Bézier: considérons une suite de n+1
points du plan: {Pi = (xi ,yi) } / i = 0 to n}, qui définit un polygone
à n côtés appelés polygone de commande. On appelle
approximation de Bernstein-

Bézier de cet ensemble de points 599, la courbe
paramétrée par:
Nous avons pris n = 3 et obtenu des courbes dites cubiques: les
courbes cubiques sont définies
en utilisant quatre points, deux points situés aux
deux extrémités de la courbe, et les deux autres sur les
deux tangentes exerçant dans une certaine mesure une attraction sur la
courbe.
Fig. 3.29 - Les 2 points et les 2 tangentes définissant
une courbe de Bézier cubique
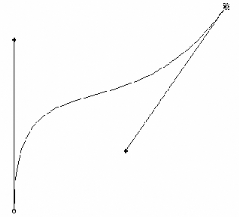
Soient t un nombre entre 0 et 1, et p(t) un point non
spécifié de la courbe. Lorsque t varie de 0
à 1, on obtient l'ensemble des points qui
constituent la courbe. Voici les équations qui permettent de
définir la courbe:
Le polynôme p(t) = ap t 3 + bp t ² + cp t +
p0
599 LANE J.M. et RIESENFELF R.F. (janvier 1980) A
Theoretical Development for the Computer Generation and display of Piecewise
Polynomial Surfaces, IEEE Trans. on PAMI, Vol. PAMI-2, No 1, p.
35-46.
où t [0, 1]
et ses coefficients:
p1 = p0 + cp / 3
p2 = p1 + (cp + bp) / 3
p3 = p0 + cp + bp + ap
L'exemple concret suivant de délimitation
morphologique reprend le cas de clients virtuels abordé au
chapitre précédent avec en premier lieu une cartographie des
clients associés à leurs fréquentations d'un point de
vente suivi de deux filtres Nagao (voir paragraphe 2.6.2.1).
Fig. 3.30 - Adresses clients associées aux
fréquentations Fig. 3.31 - suivies de deux filtres Nagao,

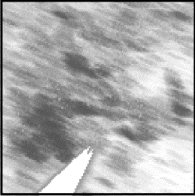
Fig. 3.32 - puis une dilatation, Fig. 3.33 - ensuite une
érosion
(transformation de fermeture),


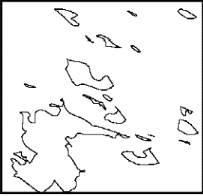
Fig. 3.34 - Une soustraction par rapport Fig. 3.35 - Enfin un
amincissement
à l'image filtrée du début (transformation
et une régularisation, des contours chapeau haut-de-forme) (grâce
aux courbes de Bézier)

A la suite de ces délimitations de zones de chalandise, il
convient de construire le modèle p-
médian avant de le résoudre ce qui signifie au
minimum, définir les noeuds du réseau (noeuds constitués
par les centres de gravité de chacune des aires formant la zone de
chalandise) et quantifier la demande associée à chaque noeud. La
construction de ce réseau est ainsi l'objet
de notre prochain paragraphe.
| 


