3.3 La construction du modèle p-médian :
détermination des centres de gravité, distances et
pondérations du modèle p-médian
La délimitation de la zone de chalandise a mis en
évidence les diverses régions de l'espace concentrant un grand
nombre de clients. Pour déterminer les coordonnées des
centres de gravité de ces régions (futurs noeuds du
modèle) et procéder à une analyse en profondeur des
caractéristiques de la clientèle (demandes du
modèle), il s'agit auparavant de définir analytiquement
ces régions, c'est-à-dire de préférence par les
coordonnées de leurs contours. Connaître d'une manière
rationnelle les frontières des régions formant la zone de
chalandise nous permettra de calculer la position de leurs centres de
gravité, futurs noeuds du modèle p- médian. L'autre
intérêt est de déterminer l'étendue de ces
régions dans lesquelles la densité de
clients est forte et de même niveau, afin d'évaluer
le niveau de la demande dans chacune de
ces aires (demande associée à chaque noeud du futur
modèle p-médian).
Plus précisément, les frontières des
régions géographiques peuvent être définies par
différents types de coordonnées comme la succession des
coordonnées, le code de Freeman, le code hexagonal ou
les points essentiels.
· la succession des coordonnées
La succession des coordonnées (i, j ) des points de
la frontière linéique s'obtient en parcourant
la frontière dans un sens ou dans l'autre. Ce codage a
l'inconvénient de nécessiter un grand nombre de données (2
x Nf, où Nf est le nombre de points de la frontière).
· le code de Freeman 600
On décrit en partant d'un point de la frontière et
en la parcourant dans un sens de convention,
les différentes orientations prises par la courbe
(vecteurs successifs), soit en général 8 orientations :
N(nord), NE (nord-est), NO (nord-ouest), O (ouest), SO (sud-ouest), S (sud), SE
(sud-est), E (est) ou bien avec moins de précision seulement 4 : N
(nord), O (ouest), S (sud), E (est). Ce type de codage ne nécessite que
Nf + 2 données distinctes (incluant les coordonnées
du point de départ, chaque élément
directionnel du codage n'étant représenté que par
un nombre restreint de bits, 4 ou 8).
· le code hexagonal (dans le cas d'une matrice [de
points images] hexagonale)
Le contour est décrit par le point de départ et 3
directions (comme pour le code de Freeman)
mais on simplifie en n'indiquant que la direction d'orientation
du segment courant par rapport
au précédent en parcourant la courbe selon
un sens de convention. Le nombre de bits nécessaire au codage
descend à 2 et nécessite le même nombre de données
distinctes que le code de Freeman.
Fig. 3.36 - Exemple de Codage Hexagonal
600 FREEMAN H. (1970) Boundary Encoding and
Processing in Picture and Processing and Psychopictrorics, Lipkin B.S. and
Rosenfeld A., Academic Press, New York, p. 241-266.
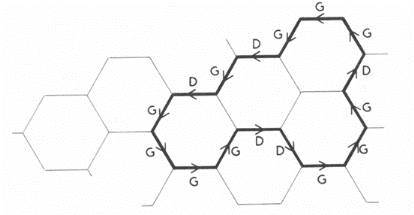
G=direction gauche et D=direction droite par rapport au segment
précédent
· les points essentiels
On cherche alors à minimiser le nombre de points de
description en approximant le contour
par une courbe enveloppante continue et dérivable
(familles de fonctions B-splines). Ce principe est surtout utilisé
dans les logiciels de CAO.
Comment connaître les coordonnées des
points formant les frontières de la zone de chalandise par
l'algorithme de description ?
La procédure de segmentation
précédente a, comme on l'a souligné, permis
d'identifier des points P(i, j) connexes formant des zones
d'équi-fréquence. La réunion de ces
différentes zones constitue l'ensemble de la zone de chalandise.
Un algorithme de description simple permet d'extraire les
coordonnées de la frontière de la zone de chalandise
à partir de la fonction caractéristique à
l'étape précédente de délimitation. En effet, pour
chaque zone de chalandise Z, on peut définir une fonction
caractéristique fZ (i, j) telle que:
P(i, j) Z , fZ (i, j) = 1 et P(i, j) Z ,
fZ (i, j) = 0
Cette fonction permet de toujours savoir si on est à
l'intérieur ou à l'extérieur de la zone. On applique
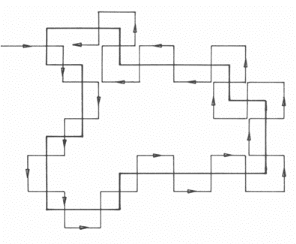
maintenant l'algorithme de suivi de contour:
1) On balaye la matrice fZ (i, j) de la fonction
caractéristique ligne par ligne jusqu'à atteindre
le point P'(i', j'), le plus haut de la zone Z :
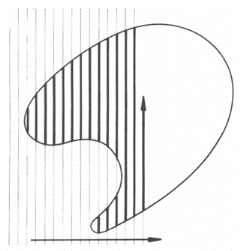
Fig. 3.37 - Exemple de parcours d'une forme à l'aide de
l'algorithme
destiné à extraire les coordonnées du
contour
2) Si on est en un point situé à
l'intérieur de la zone Z, [fZ (i, j) = 1] , tourner
à droite puis
avancer d'un cran dans cette direction (d'une colonne ou d'une
ligne).
3) Si on se trouve en un point situé à
l'extérieur de la zone Z, [fZ (i, j) = 0] , tourner à gauche
puis avancer d'un cran dans cette direction (d'une colonne ou d'une ligne).
4) Interrompre l'algorithme dès que l'on atteint à
nouveau le point de départ.
Fig. 3.38 - Exemple de parcours de frontière de zone de
chalandise à l'aide de l'algorithme
On enregistre ainsi les directions successives prises par
l'algorithme de suivi ce qui donne une description du contour sous la forme
d'une chaîne ascii en codes de Freeman :
[
E,S,E,S,O,S,O,S,E,S,E,N,E,N,E,S,E,N,E,S,E,N,O,N,E,N,O,S,O,N,E,N,O,S,O,N,O,S,O,N,E,N,O,S,O
]
Ce codage a aussi le grand avantage de pouvoir tout de suite
déterminer très simplement la surface géographique Sg de
la zone de chalandise par l'algorithme suivant en supposant que la chaîne
en code de Freeman s'écrive [a1, a2,...ai,...,an] :
1) Au départ; u = 0 et t =0
2) De i = 1 à n Faire
A) Si ai = Nord Alors
t = t + 1 Sinon Aller en B)
|
B) Si ai = Sud
|
Alors
|
u =
|
u + t
|
Sinon Aller en C)
|
|
C) Si ai = Ouest
|
Alors
|
t =
|
t - 1
|
Sinon Aller en D)
|
D) Si ai = Est Alors
u = u - t
3) Sg = u x S
où la valeur du paramètre u à la
fin de la procédure est le nombre de points contenus dans la zone de
chalandise considérée, t un paramètre de comptage et S la
superficie géographique unitaire d'un point.
Comment calculer les coordonnées des centres de
gravité des aires de chalandise ?
Les coordonnées des contours des aires
délimitées vont nous permettre d'accéder simplement aux
coordonnées des centres de gravité des différentes
aires constitutives de la zone de chalandise globale. Le repérage
de ces centres de gravité correspondant aux futurs noeuds du
modèle p-médian dans notre algorithme, donnera aussi par un
simple calcul de longueur, les distances de chaque segment du réseau (de
plus, si la zone de chalandise est très fragmentée et pas du
tout rassemblée, la moyenne des distances entre les centres de
gravité fournira une mesure de l'éloignement des noeuds). Une
question basique que l'on peut se poser est de savoir pourquoi, dans la
recherche d'une localisation optimale unique à partir de l'adresses de
clients,
on ne procèderait pas directement au calcul du centre
de gravité (localisation moyenne) par rapport à ces
mêmes clients pour choisir un emplacement bien centré de
son futur site. Considérons la cartographie suivante qui montre un
ensemble de clients potentiels représentés
par des points (voir figure 3.39). Le centre de gravité de
la totalité des clients est au point J, en pleine campagne. On remarque
que J est très éloigné de l'ensemble majoritaire des
clients de
l'agglomération rassemblés dans le cercle et donc
du potentiel commercial le plus intéressant.
Fig. 3.39 - Ensemble de clients potentiels
représentés par des points

Le fait de pratiquer un filtrage, par exemple
médian, et de délimiter la zone de chalandise (zone dense
de clients) permet de ne prendre en compte que les régions ayant
un potentiel commercial suffisant. L'analyse de localisation fait donc
abstraction de tous les clients "saupoudrés" dans l'espace et dont
la prise en compte risque de perturber les calculs. On voit
sur la cartographie suivante la zone de chalandise principale
délimitée par filtrage: le centre
de gravité est bien centré sur cette zone à
potentiel et non plus décalé en pleine campagne
(voir figure 3.40).

Fig. 3.40 - Centre de gravité d'une zone de chalandise
délimitée
Le centre de gravité convient donc bien pour
représenter la position moyenne d'une entité dans l'espace
en l'occurrence ici la position de l'agglomération (centre d'un futur
noeud du p- médian), mais celui-ci n'est pas compatible avec les
contraintes du modèle p-médian pour déterminer une
localisation optimale. D'autre part, au niveau régional ou national, il
est plus significatif de comparer entre eux les centres de
gravité des aires mises en évidence par le processus de
délimitation que les centres de gravité calculés
sur l'ensemble des points appartenant aux aires (localisation moyenne des
clients). Le centre de gravité d'une aire est en effet
théoriquement le point à partir duquel on parcourt la distance la
plus courte en moyenne
pour l'atteindre à partir de tous les autres points de
l'aire (point le plus accessible). L'aire est,
on le rappelle, constituée d'une masse de
clients de densité homogène obtenue par lissage (filtrage).
Le centre de gravité de l'aire qui circonscrit l'esnsemble des clients
ne correspond pas forcément à la moyenne des localisations des
clients (voir figure 3.41). Prendre un tel centre de gravité des
adresses des clients au lieu de celui de la surface de l'aire totale revient
aussi à ne pas tenir compte de ce lissage destiné à
éliminer une partie des erreurs d'enquête (adresses manquantes ou
fausses adresses, clients ayant déménagé).
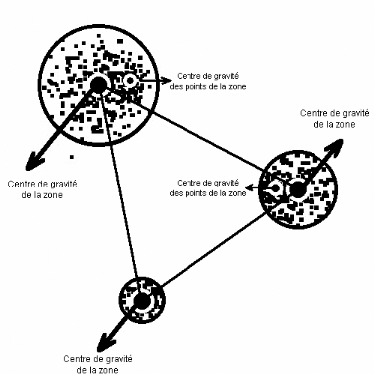
Fig. 3.41 - Les centres des aires et ceux des points appartenant
à ces mêmes aires
Le centre de gravité des aires est également
très intéressant dans le cas de desserte de transport
interurbaine qu'il s'agisse de transport de voyageurs (gare Sncf ou gare
routière) ou
de transport de marchandises (entrepôt) : on cherche en
effet le point le plus central possible
au sein d'une aire pour implanter un entrepôt
destiné à recevoir des marchandises de gros, entrepôt
à partir duquel on effectuera des livraisons au détail
vers des clients situés en périphérie de ce centre
local de distribution.
Le repérage du centre de gravité au
niveau global sur un ensemble d'adresses clients ne permet d'obtenir
qu'une position moyenne pour une localisation sans tenir compte des
barrières naturelles ou des sites géographiquement inaccessibles.
En outre, cette méthode est complètement inadaptée
à la recherche de localisations multiples.
Ayant déterminé précédemment les
coordonnées des points décrivant la frontière de la
zone
de chalandise, les coordonnées de son centre de
gravité seront tout simplement la moyenne
des coordonnées de ces points de contour.
Cependant, d'une manière plus générale, le
centre de gravité G d'une zone Z composée de n points clients P1,
..., Pn auxquels sont affectées des fréquentations (ou une
demande) f1, ..., fn
est tel que :
n
[ fu GPu] = 0
u=1
Considérons la fonction caractéristique
fZ (i, j) de la zone de chalandise Z,
préalablement
définie par:
P(i, j) Z , fZ (i, j) = 1 et P(i, j) Z , fZ (i, j) = 0
Pour déterminer G le plus simplement possible sur un
espace de valeurs discrètes, l'expression
de la fréquentation étant alors sous la forme f(i,
j) pour un point P de coordonnées P(i, j), on utilisera la relation:
m p
[fz(i, j) f(i, j) GPij] = 0
i =1
j =1
Avec m, le nombre de lignes de la matrice des
fréquentations associées à l'espace
géographique 2D considéré et p son nombre de
colonnes.
A noter que comme dans chaque aire, la
fréquentation est environ la même (f(i, j) =
constante), l'équation précédente se
réduit à:
p
m [fz(i, j)
GPij ] = 0
i = 1 j = 1
Comment déterminer les distances entre les noeuds du
modèle p-médian ?
Les distances des segments du modèle p-médian
reliant noeuds ou centres de gravité des zones sont calculées
soit en utilisant la distance euclidienne classique, soit en
déterminant les distances routières ou temps de
parcours (par exemple à l'aide d'un logiciel comme
AutorouteExpress de Microsoft), soit encore en utilisant la notion de distance
psychologique
(dij - nj) introduite dans un modèle p-médian
"généralisé" (voir § 2.3.1).
Comment déterminer le niveau de la demande
associé à chaque noeud ?
Cette même fonction caractéristique permet en
outre de fournir les propriétés marketing ou
socio-économiques liées aux zones et donc d'obtenir le niveau de
demande dans chaque zone (demandes dans le modèle p-médian
pondéré): soit V une variable dont la valeur évolue dans
l'espace total de la zone de chalandise. V est donc fonction du
point P(i,j) de l'espace géographique et s'écrit V(i,j).
La variable V peut être simplement le chiffre d'affaires
escompté dans la zone pour un produit ou un service spécifique
(niveau de la demande), une variable socio-économique (taux de
possession d'un véhicule, PCS, pouvoir d'achat moyen), une mesure de la
contribution locale à la performance (fréquentation comme dans
l'exemple
qui suit, chiffre d'affaires ou bénéfices
perçus par des clients en P(i,j)), un paramètre
environnemental (densité de la concurrence en P, places de parking,
circulation automobile),... Pour connaître la valeur de V à
l'intérieur d'une zone soit en somme, soit en moyenne, on
utilise encore la fonction caractéristique fZ(i, j). Pour une variable
V(i, j) à sommer comme
par exemple le nombre de places de parking dans la zone Z ou le
chiffre d'affaires tiré de la
zone Z, on aura Vz, la somme des V(i, j) sur l'ensemble de la
zone Z comme étant:
m p
Vz =
[f z (i, j)
i = 1 j = 1
V(i, j) ]
Pour une variable V(i, j) à étudier en valeur
moyenne comme par exemple le pouvoir d'achat
moyen dans la zone Z, on aura pour expression de Vz, la moyenne
des V(i, j) sur l'ensemble
de la zone Z:
m p
[f Z (i, j)
i =1 j =1
V(i, j) ]
VZ = m p
[f z (i, j) ]
i =1 j =1
Considérons la variable N(i, j) représentant le
nombre de clients en chaque point P(i,j). Alors
le pourcentage de clients contenu dans la zone de chalandise
à forte densité de clientèle par rapport au nombre de
clients total, est donné par:
p
Z
m [f
(i, j) N(i, j) ]
i =1 j =1
m
p
[N(i, j) ]
100
i =1 j =1
Si la zone de chalandise Z est morcelée en plusieurs
aires Z1,...Zh, il suffit de faire le calcul
sur chaque région et de sommer pour avoir le
pourcentage total, une alternative étant de définir la
fonction caractéristique réunissant toutes ces régions.
| 


