Chapitre 5
Mise en oeuvre d'un système rapide d'aide
à la décision de localisation
Introduction
Le modèle p-médian ayant été
construit en particulier grâce aux puissantes fonctions
de filtrage du traitement du signal, nous débouchons alors
sur un problème classique
de résolution d'un modèle de
localisation-allocation. Ainsi, comme nous l'avons vu, les algorithmes
classiques d'un tel modèle sont bien connus :
l'algorithme flou, l'algorithme de voisinage, la résolution par les
multiplicateurs de Lagrange ou encore l'algorithme génétique.
Mais, appliqué à notre modèle d'une
complexité divisée par rapport au problème initial d'un
facteur 400, la résolution en sera d'autant plus rapide
(il y a avait en effet 10211 adresses au départ et nous
n'avons désormais plus qu'un réseau de 25 noeuds). Une ou
plusieurs régions géographiques appartenant à la zone de
chalandise parmi les 25, seront alors préconisées pour
être le siège d'implantations optimales de magasins de
produits biologiques. On pourra juger cependant que la précision
obtenue n'est pas suffisante puisqu'elle se cantonne à indiquer
seulement, parmi 25 quartiers, les plus intéressants. Nous montrerons
que cette précision peut être largement dépassée,
comme le prévoit notre algorithme. Le même processus de
dilatation, de filtrage sera réitéré au niveau des
quartiers préconisés afin d'obtenir de nouveaux modèles
p-médian plus fins qui seront ultérieurement résolus par
les mêmes heuristiques classiques. La précision atteindra, on le
verra alors, un positionnement au
niveau des voies de circulation à quelques numéros
de rue près.
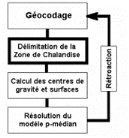
5.1 Résolution du modèle p-médian par
l'algorithme flou et l'algorithme de voisinage
Algorithme flou et algorithme de voisinage nous
donnent exactement les mêmes résultats quant aux localisations
optimales pour p variant de 1 à 25. Ils nous indiquent tout
d'abord que le noeud 10 est le plus indiqué pour
une
implantation unique. En ce qui concerne l'algorithme de
voisinage, une substitution est
pratiquée à la dernière itération
pour en améliorer les résultats. Ceux-ci sont
résumés dans le tableau suivant:
|
Nombre de
Localisations
|
Noeuds d'Implantation des Points de Vente
|
Fonction
Objectif
|
Distance
Maximale à Parcourir
|
|
2 loc.
|
1, 10
|
3205268
|
472
|
|
3 loc.
|
1, 10, 18
|
2512282
|
284
|
|
4 loc.
|
1, 6, 10, 18
|
1908833
|
172
|
|
5 loc.
|
1, 6, 10, 18, 22
|
1507518
|
172
|
|
6 loc.
|
1, 6, 10, 12, 18, 22
|
1177979
|
172
|
|
7 loc.
|
1, 6, 9, 10, 12, 18, 22
|
981793
|
145
|
|
8 loc.
|
1, 6, 9, 10, 12, 18, 22, 23
|
808933
|
145
|
|
9 loc.
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679238
|
145
|
|
10 loc.
|
1, 3, 7, 9, 10, 12, 15, 18, 22, 23
|
561933
|
114
|
|
11 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 18, 22, 23
|
471987
|
110
|
|
12 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
408799
|
110
|
|
13 loc.
|
1, 2, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
351929
|
86
|
|
14 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20,
22
|
302977
|
86
|
|
15 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22,
25
|
257139
|
57
|
|
16 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22,
25
|
212818
|
57
|
|
17 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21, 22,
25
|
177618
|
57
|
|
18 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21,
22, 23, 25
|
147852
|
57
|
|
19 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 23, 25
|
117471
|
41
|
|
20 loc.
|
1, 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20,
21, 22, 23, 25
|
91313
|
34
|
|
21 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
20, 21, 22, 23, 25
|
67953
|
34
|
|
22 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
19, 20, 21, 22, 23, 25
|
48579
|
34
|
|
23 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
25
|
30355
|
31
|
|
24 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 24,
23, 25
|
13026
|
26
|
|
25 loc.
|
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22,
23, 24, 25
|
0
|
0
|
Tableau 5.1 - Localisations optimales données par les
algorithmes flou et de voisinage
Fig. 5.1 - La mise en oeuvre de l'algorithme flou sur le logiciel
Sitation
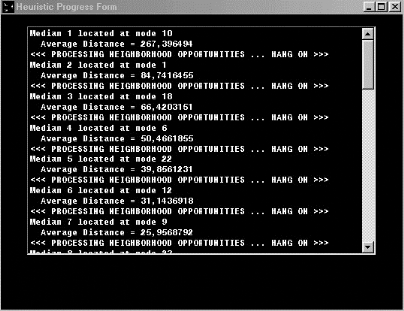
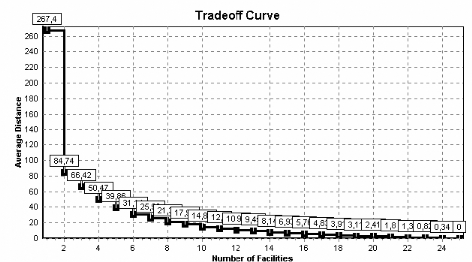
La distance moyenne à parcourir pour les clients en
fonction du nombre de magasins créés est donnée par le
graphique 5.2 :
Fig. 5.2 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts:
|
|



