5.2 Résolution du modèle p-médian par
les multiplicateurs de Lagrange
Rappelons que les multiplicateurs de Lagrange sont des
variables à partir desquelles on construit une fonction
appelée lagrangien et notée L, fonction utilisée dans les
problèmes de recherche de l'extremum lié d'une fonction f
(optimisation sous contraintes). Dans ce type de problème
général, les variables xi sont astreintes à
vérifier m relations :
hk (x1,..., xi,..., xn) = 0
(pour k = 1,....., m)
Une condition nécessaire pour que f soit minimale
est qu'il existe m multiplicateurs de

Lagrange tels que :

Ces relations équivalent à l'annulation des
dérivées du premier ordre du lagrangien défini par :
Dans notre cas, la fonction à minimiser (voir §
2.2.1.2) est la fonction objectif relaxée par les
multiplicateurs de Lagrange i :
( ai dij + i ) xij +
i j i
i (1)(1)
et les contraintes sont :
xij = 1, i, (2)
i
xij yj, i, j, (3)
yj = p, (4)
j
xij, yj {0,1}, i, j (5)
où
ai : la demande au noeud i,
di,j : la distance du noeud i au noeud j,
p : le nombre d'activités à localiser,
xi,j = 1, si le noeud i est assigné à
l'activité j et 0 autrement,
yj = 1, si l'activité j est ouverte et 0 autrement.
Le nombre d'itérations a été fixé
à 400, la valeur minimale du paramètre lambda à
0,00000001
et le nombre d'échecs avant de modifier ce
paramètre (par pas de 0,3) à 36. Un algorithme
d'amélioration par substitution a été mis en oeuvre
ensuite pour en améliorer les résultats.
Les résultats obtenus ont été les
suivants:
|
Nombre de
Localisations
|
Noeuds d'Implantation des Points de Vente
|
Fonction
Objectif
|
Distance
Maximale à
Parcourir
|
|
2 loc.
|
1, 10
|
3205268
|
472
|
|
3 loc.
|
1, 10, 18
|
2512282
|
284
|
|
4 loc.
|
1, 6, 10, 18
|
1908833
|
172
|
|
5 loc.
|
1, 6, 10, 18, 22
|
1507518
|
172
|
|
6 loc.
|
1, 6, 10, 12, 18, 22
|
1177979
|
172
|
|
7 loc.
|
1, 6, 9, 10, 12, 18, 22
|
981793
|
145
|
|
8 loc.
|
1, 6, 9, 10, 12, 18, 22, 23
|
808933
|
145
|
|
9 loc.
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679238
|
145
|
|
10 loc.
|
1, 3, 7, 9, 10, 12, 15, 18, 22, 23
|
561933
|
114
|
|
11 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 18, 22, 23
|
471987
|
110
|
|
12 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
408791
|
110
|
|
13 loc.
|
1, 2, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
351929
|
86
|
|
14 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20,
22
|
302977
|
86
|
|
15 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22,
25
|
257139
|
57
|
|
16 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22,
25
|
212818
|
57
|
|
17 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21, 22,
25
|
177618
|
57
|
|
18 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 25
|
147237
|
41
|
|
19 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 23, 25
|
117471
|
41
|
|
20 loc.
|
1, 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20,
21, 22, 23, 25
|
91313
|
34
|
|
21 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
20, 21, 22, 23, 25
|
67953
|
34
|
|
22 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
19, 20, 21, 22, 23, 25
|
48579
|
34
|
|
23 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
25
|
30355
|
31
|
|
24 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
24, 25
|
13026
|
26
|
|
25 loc.
|
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22,
23, 24, 25
|
0
|
0
|
Tableau 5.2 - Localisations optimales données par
l'algorithme des multiplicateurs de Lagrange
Pour 18 localisations, le noeud 14 a été choisi
à la place du 23, mais les résultats redeviennent
à nouveau équivalents aux noeuds choisis par
l'algorithme de voisinage ou l'algorithme flou pour 19 implantations à
créer : le choix de l'algorithme des multiplicateurs de Lagrange pour
18 localisations est néanmoins meilleur étant
donné que la fonction objectif (147 237 au lieu
de 147 852) est, dans ce cas, plus faible et que la distance
maximale à parcourir en moyenne par les consommateurs est
également moins importante (41 au lieu de 57).
Fig. 5.3 - Pour 4 localisations: aires de potentiel commercial
associées aux points de vente (en gras)
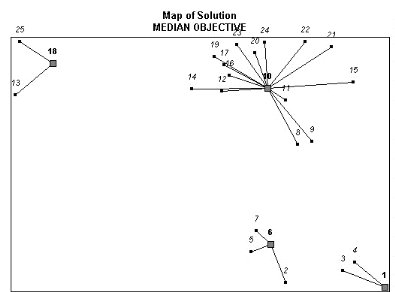
Le schéma précédent montre clairement
la supériorité stratégique de la localisation en 10
:
elle couvre nettement mieux les aires de clientèles que
les autres sites.
|
|



