3.5 Un exemple de construction d'un modèle
p-médian par traitement du signal
Reprenons l'exemple du magasin avec les clients virtuels
associés à leurs fréquentations du chapitre
précédent :
Fig. 3.51 - Adresses clients associées aux
fréquentations Fig. 3.52 - La délimitation des zones par filtres
médian et Sobel


En calculant les coordonnées (X,Y) du
centre de gravité et la valeur moyenne des
fréquentations (ainsi que divers paramètres
géométriques) de chaque aire selon les méthodes
décrites ci-dessus, on obtient la cartographie avec chaque aire
numérotée et les deux tableaux
de valeurs suivants (3.1 et 3.2).
628 KAUFMANN P.J., DONTHU N. et CHARLES M.B.
(2000) Multi-unit Retail Site Selection Processes : Incorporating Opening
Delays and Unidentified Competition, Journal of Retailing, Vol.76(1),
p. 113-127
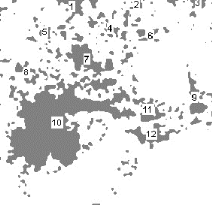
Fig. 3.53 - Numérotation des aires de chalandise
Tableau 3.1 - Paramètres géométriques des 12
aires de la zone de chalandise obtenus après délimitation
|
Aire
|
Superficie
|
X
|
Y
|
Périmètre
|
Diamètre Ds
|
Epaisseur De
|
Angle
|
|
1
|
346
|
87
|
9
|
142
|
24
|
20
|
138
|
|
2
|
110
|
165
|
6
|
60
|
13
|
10
|
49
|
|
3
|
156
|
239
|
4
|
59
|
18
|
10
|
175
|
|
4
|
194
|
134
|
37
|
88
|
19
|
12
|
129
|
|
5
|
124
|
55
|
41
|
64
|
13
|
11
|
53
|
|
6
|
143
|
182
|
45
|
89
|
17
|
10
|
31
|
|
7
|
1048
|
105
|
74
|
236
|
52
|
25
|
152
|
|
8
|
322
|
32
|
90
|
148
|
28
|
14
|
134
|
|
9
|
467
|
235
|
122
|
147
|
45
|
13
|
102
|
|
10
|
7594
|
70
|
152
|
1139
|
134
|
77
|
34
|
|
11
|
467
|
180
|
137
|
213
|
28
|
21
|
144
|
|
12
|
689
|
183
|
167
|
233
|
45
|
19
|
1
|
Tableau 3.2 - Paramètres marketing des 12 régions
de la zone de chalandise obtenus après délimitation
|
Aire
|
Fréquentation
Moyenne
|
Valeur
Modale
|
Maximum des
Fréquentations
|
|
1
|
143
|
128
|
192
|
|
2
|
134
|
128
|
173
|
|
3
|
145
|
128
|
190
|
|
4
|
135
|
128
|
173
|
|
5
|
136
|
128
|
173
|
|
6
|
136
|
128
|
173
|
|
7
|
164
|
192
|
192
|
|
8
|
133
|
128
|
173
|
|
9
|
157
|
128
|
192
|
|
10
|
161
|
173
|
192
|
|
11
|
134
|
128
|
173
|
|
12
|
147
|
128
|
192
|
Les valeurs de X et de Y nous donnent les coordonnées des
centres de gravité de chaque aire
de chalandise et donc les noeuds du réseau
p-médian. La demande en chaque noeud peut être
caractérisée soit par la fréquentation, soit par la
demande globale dans l'aire égale à la
fréquentation moyenne par la superficie (les fréquentations
moyennes représentent les valeurs
de la fréquentation au sein des aires qui
possède, par notre définition, le caractère d'avoir un
niveau homogène). L'intérêt de prendre la demande globale
dans l'aire comme valeur de la demande en chacun des noeuds est que celle-ci
est révélatrice à la fois du niveau moyen de
fréquentation dans l'aire considérée et de
l'étendue de cette aire, et constitue ainsi une mesure
intéressante du potentiel commercial au voisinage du centre de
gravité. Il est à noter que ces fréquentations
associées aux adresses des clients peuvent être les
fréquentations effectives d'un point de vente ou d'un ensemble de
points de vente existants dans le cas où l'on voudrait
réorganiser un réseau de magasin en tirant parti de
l'expérience commerciale acquise. Mais,
ces fréquentations tout aussi bien susceptibles
d'être tirées d'une enquête marketing en demandant
à un échantillon de clients potentiels répartis dans
l'espace s'ils comptent acheter
tel ou tel produit ou service et à quel rythme. Pour
caractériser la demande, nous aurions aussi
bien pu prendre en compte d'autres paramètres que
les fréquentations comme le volume d'affaires ou même les
bénéfices.
La dernière étape avant d'obtenir le réseau
p-médian complet est de lier les noeuds en fonction
du réseau de routes existant et d'évaluer les
distances kilométriques (ou de mesurer les temps
de parcours) pour évaluer les "coûts" de
déplacement.
Fig. 3.54 - Le p-médian modélisé
après délimitation de la zone de chalandise et calcul des
centres de gravité et fréquentations moyennes. La valeur de
fréquentation au sein des aires est ici prise comme valeur de la
demande aux noeuds.
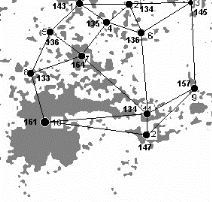
Ensuite, peut alors s'effectuer la résolution du
modèle p-médian (simplifié) selon les méthodes
existantes. En utilisant par exemple la méthode de
Goldman629 (voir chapitre I) pour la recherche d'une
localisation proche de l'optimale, on trouve que l'aire 7 avec sa
fréquentation
de 164 est un site convenable pour l'implantation d'un
magasin. En admettant que nous ne soyons pas encore satisfaits de la
précision du lieu d'implantation (dans l'aire 7), notre nouvel
algorithme associant le p-médian et le traitement du signal
(exposé au paragraphe 4.2.1) nous
demande alors d'effectuer la même démarche au sein
de cette aire 7, à savoir une délimitation
629 GOLDMAN J.L. (1971) Optimal Center Location in
Simple Networks; Transportation Science 5, 212-221.
par filtrage et une analyse des intra-aires de chalandise pour
constituer un nouveau réseau p-
médian plus petit occupant l'aire :

Fig. 3.55 - L'aire 7 agrandie

puis un filtrage médian (les fréquences sont
très semblables):
Fig. 3.56 - L'aire 7 filtrée par un filtre
médian

une délimitation par filtrage Sobel:
Fig. 3.57 - L'aire 7 délimitée par un filtre
Sobel
puis un nouveau calcul de centres de gravité et une
évaluation des fréquentations intra-aires:


Fig. 3.58 - Les éléments de l'aire 7
numérotés après délimitation
pour constituer le nouveau réseau p-médian:
Fig. 3.59 - Le réseau p-médian correspondant
à l'aire 7
Sa résolution montre que le site commercial doit non
seulement se situer dans l'aire 7 mais aussi plutôt dans la sous-aire
7.2.
| 


