Géomarketing : localisation commerciale multiple

3.6 Utiliser toutes les sources d'informations commerciales disponibles

L'intérêt du traitement du signal associé à un modèle de localisation-allocation tel que le p- médian réside aussi pour le manager dans les nouvelles perspectives offertes pour manipuler

de façon souple des informations de sources d'extraction variées. Les bases de données d'adresses de consommateurs potentiels construites par enquête ou déduites des modes de paiement servent comme on l'a vu, à alimenter le modèle après une phase de géocodage et de délimitation. Mais rien n'empêche non plus d'introduire des informations déjà mises en forme comme des cartes de données statistiques en format électronique ou même sur support imprimé. L'exemple suivant nous montrera qu'il est possible d'effectuer une étude d'implantation sans même passer par la fastidieuse étape de géocodage d'adresses, mais

simplement en reprenant des documents glanés au fil de ses lectures.

Exemple de l'implantation d'activités commerciales au niveau national

Le traitement du signal peut aussi s'attaquer à traiter des informations issues de sources variées comme par exemple des cartographies sur support papier, qui seront directement intégrées dans un modèle p-médian. En témoigne l'exemple de cette carte représentant des densités de population en 2000, carte publiée dans le supplément "l'atlas des régions"⁶³⁰ du magazine les Echos.

Une première phase consiste à acquérir l'information, c'est-à-dire à scanner le document de la même manière que précédemment. Les données d'enquête ont été saisies pour constituer une base de données, puis ont été géocodées. Le procédé consiste alors à appliquer à ces données scannées le même traitement de filtrage et de convolution par un filtre Sobel pour en extraire

les contours les plus marquants, en l'occurrence ceux des bassins de population. Cet exemple illustre bien la souplesse et la rapidité du traitement du signal qui permet d'intégrer n'importe quel document dans une logique p-médian (ou autre modèle de localisation-allocation) sans

même ici perdre de temps ou d'énergie à saisir les données !

⁶³⁰ LES ECHOS (2000) L'atlas des Régions Tome 1, Les Echos, réalisé en collaboration avec l'Insee.

Fig. 3.60 - Carte de France des densités de population en 2000 ⁶³¹

Fig. 3.61 - La carte traitée par un filtre médian, Fig. 3.62 - puis délinée par filtre Sobel

⁶³¹ LES ECHOS (2000) L'atlas des Régions Tome 1, Les Echos, réalisé en collaboration avec l'Insee.

Fig. 3.63 - Les zones numérotées et analysées

Nous obtenons tout de suite les caractéristiques de bassins de population en terme de

localisation de leur centre d'inertie et de leur étendue (voir tableau 3.3). Il est à noter que nous avons pris comme exemple une carte de densité de population, mais que n'importe quelle autre carte issue d'une quelconque source électronique ou papier aurait pu convenir, cela en fonction des besoins de l'analyse.

Supposons que la France ne compte pas encore d'hypermarchés et qu'un grand groupe décide

d'y créer 10 magasins. Où faudrait-il les installer compte tenu des bassins de population ? Le

p-médian (ou plutôt 10-médian) va nous donner ici encore une fois rapidement la réponse

grâce à l'étape précédente de délimitation des zones par traitement du signal. La résolution du modèle avec les paramètres X, Y et la superficie, pour une distance limite raisonnable de parcours pour les consommateurs de 50 miles, nous apprend très rapidement que les meilleures implantations sont en : 1 (Lille-Roubaix), 6 (Paris et Région Parisienne), 9 (Strasbourg), 18 (Tours), 24 (Lyon), 33 (Bordeaux), 35 (Nice), 36 (Montpellier et la côte), 37 (Marseille et Région) et 38 (la distance maximale à parcourir est alors en théorie 645 pour une fonction objective de 10 253 440). Dans le cas où un nouvel hypermarché viendrait à s'installer, il lui faudrait se placer en 5. Les premiers hypermarchés ont en effet été créés dans

ces régions fortement peuplées à partir des années 60.

Tableau 3.3 : Les caractéristiques des 43 aires de population détectées par traitement du signal

ZONE	Superficie	X	Y	Longueur	Majeur	Mineur	Angle
1	13272	1237	168	1050	177	98	155
2	740	1373	213	163	50	19	29
3	2443	952	420	371	69	45	96
4	870	1211	409	198	58	19	63
5	2680	1706	433	308	89	38	91
6	18179	1135	531	1324	165	145	102
7	1256	733	454	245	45	35	70
8	1435	1815	448	290	68	27	174
9	4594	1951	557	528	116	51	59
10	1356	1721	556	230	51	34	133
11	753	97	599	132	49	20	13
12	875	1908	680	142	45	25	42
13	1803	518	696	225	54	42	162
14	850	810	731	143	41	27	106
15	2021	1900	749	263	65	41	126
16	922	1076	753	134	41	29	4
17	1389	1837	811	307	55	32	89
18	1132	693	845	155	39	37	68
19	1495	885	874	198	44	43	12
20	805	1710	883	165	48	21	37
21	2452	532	896	253	61	51	159
22	831	827	1041	159	42	25	104
23	1065	1780	1108	301	55	24	63
24	7045	1553	1230	606	114	79	135
25	870	1746	1186	140	43	26	117
26	1770	1273	1229	239	69	33	107
27	1046	971	1218	161	43	31	38
28	827	1717	1249	160	51	21	100
29	706	792	1259	114	37	25	27
30	2390	1475	1293	339	64	48	20
31	2627	1690	1339	443	60	56	116
32	1046	1560	1410	201	54	25	112
33	3138	669	1436	300	76	53	180
34	2633	1579	1635	334	59	57	66
35	4155	1930	1690	522	149	36	41
36	4911	1434	1705	626	168	37	36
37	8558	1685	1766	870	162	67	148
38	3642	990	1731	303	77	60	58
39	1524	1594	1725	274	61	32	71
40	1547	1315	1782	306	68	29	8
41	893	696	1788	165	37	31	146
42	906	1266	1819	189	41	29	33
43	1992	1247	1936	254	53	48	111

Fig. 3.64- Pour 10 localisations: zones de potentiel commercial associées aux points de vente en gras

(en ignorant la distance limite de parcours des 50 miles)

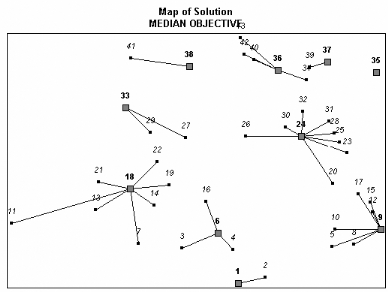
Il est à noter cependant qu'avec 10 hypermarchés, seulement 40,6 % de la demande est couverte. D'autre part, on s'aperçoit que, compte-tenu d'une distance limite de 50 miles que les consommateurs seraient prêts à parcourir, les hypermarchés ne couvrent en terme d'offre que leur propre aire d'implantation soit 10 aires sur 43, ces aires étant en France parmi les plus peuplées. Si cette logique d'implantation préoccupait une activité pour laquelle les consommateurs sont prêts à parcourir une plus grande distance comme par exemple celle des parcs d'attraction qui doivent aussi se placer au plus près de leurs clients, nous aurions obtenu

les mêmes résultats mais avec un taux de couverture de 100 % (en supposant que les clients soient prêts à parcourir deux cents ou trois cents kilomètres) : les zones de population sont en

effet éloignées les unes des autres ce qui ne les met pas en concurrence.

Fig. 3.65 - Distance moyenne à parcourir en fonction du nombre de magasins ouverts

(en ignorant la distance limite de parcours des 50 miles)

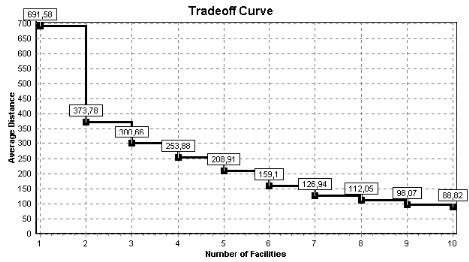
Conclusion

Nous avons vu dans ce chapitre que les principes du traitement du signal pouvaient être introduits dans une problématique de gestion et en particulier la recherche de localisations commerciales optimales. Dans ce cadre, nous avons présenté un nouvel algorithme composé

de quatre étapes en l'occurrence :

- une phase d'acquisition des données constituées par les adresses des clients qui seront géocodées afin d'obtenir une cartographie représentant l'ensemble des clients potentiels.

- un pré-traitement des données destiné à éliminer par un filtrage les imperfections de la base

de données d'adresses entraînées par exemple par des adresses incomplètes, de mauvaises saisies, des erreurs d'échantillonnage,.... Cette étape comprend en deuxième lieu la phase de traitement ou la mise en forme des données à proprement parler qui s'attache dans notre problématique à détecter par une convolution avec un filtre du type Sobel et un sous- algorithme, les frontières de la zone de chalandise,

- l'exploitation des résultats qui permet de spécifier les caractéristiques propres de la zone de chalandise, c'est-à-dire les paramètres géométriques qui vont nous servir à construire le modèle p-médian (coordonnées des centres de gravité de chaque aire composant la zone de chalandise correspondant aux noeuds du réseau et la surface de ces aires mesurant la demande).

- la résolution du modèle ainsi élaboré par les heuristiques bien connues de résolution du p- médian.

Nous avons déjà laissé entrevoir à travers quelques exemples, les avantages d'un tel mode de recherche de localisations optimales à savoir la rapidité, la souplesse d'utilisation et la démonstrativité. La deuxième partie nous donnera l'occasion de vérifier ces avantages sur des exemples concrets portant sur la filière de distribution des produits biologiques, et en

particulier l'exactitude de la méthode, sa rapidité, sa précision et sa capacité à traiter de larges

bases de données d'adresses clients pour la recherche de localisations proches de l'optimal. Pour introduire ces exemples, nous allons dans un premier temps établir un bilan du marché des produits bio en France et dans le monde, puis présenter les différents modes de distribution de ces produits pour illustrer enfin le fonctionnement de notre algorithme avec le

cas particulier de la localisation de points de vente de produits biologiques dans l'Ouest

parisien.