Chapitre 3 :
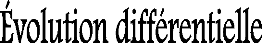
«If evolution really works, how come mothers only have
two hands? »
Milton Berle
1. Chapitre 3 Évolution
différentielle
38
Introduction
Évolution Différentielle (ED) est une
heuristique de recherche introduite par Storn et Price en 1997. C'est un
algorithme d'optimisation globale simple mais très efficace. Et qui fut
initialement créé pour résoudre des problèmes
continus. L'ED est aussi devenu un outil puissant pour résoudre les
problèmes d'optimisation qui se posent dans les applications
financières (pour l'ajustement des modèles sophistiqués et
pour effectuer la sélection du modèle) [Ardia, Boudt, 2011] et
dans les applications en temps réelle [Draa, 2011].
Dans ce qui suit, nous expliquons l'algorithme à
évolution différentielle, nous donnons ses principes, ses
variantes, ses avantages et ses limites.
2. Principe de l'évolution
différentielle
Évolution différentielle a été
conçue comme une méthode de recherche parallèle, directe,
et stochastique. L'idée générale de cet algorithme est
basée sur l'utilisation d'une nouvelle stratégie de mutation.
Elle consiste à ajouter la différence vectorielle
pondérée entre deux individus à un autre. Ensuite, une
opération de croisement entre l'individu mutant et l'individu
correspondant de la population aura lieux. Finalement, une sélection
gloutonne entre ces deux, le père et le fils, va décider lequel
des deux, ayant la meilleure fitness, survivra dans la prochaine
génération [Draa, 2011].
Dans sa version de base il existe trois paramètres : la
taille de la population NP, le taux de croisement CR et le
facteur de différence F.
Les individus (solutions) sont représentés par
des vecteurs M-dimensionnels de valeurs réelles, où M est le
nombre des paramètres à optimiser et NP est la taille de
la population. Un algorithme à évolution différentielle
peut être présenté comme suit [Ston, price, 1997] :
2.1. Mutation différentielle
Une opération de mutation consiste à
créer un nouvel individu fils correspondant à un individu
père à partir de trois autres individus choisis
aléatoirement selon l'équation (3.1) [Ston, price, 1997] :
, #177;1 = 1, #177; ( 2, 3, ) (3.1)
Où : i, r1, r2, r3 {1,...... NP} sont
des entiers mutuellement différents, et F est un facteur
constant réel positif servant à contrôler la
variation différentielle ( 2, 3, ).
Chapitre 3 Évolution différentielle
Le principe de cette mutation est illustré dans la figure
3.1.
2.2 Croisement différentielle
Le croisement est introduit en vue d'augmenter la
diversité de la population, il combine l'individu mutant obtenu par
l'opération de mutation avec l'individu cible pour
générer
un individu d'essai selon l'équation (3.2) [Ston, price,
1997] :
, 0,1 > (0, ) . (3.2)
39
,
Où : (0, 1) est un nombre aléatoire entre
0 et 1, et CR [0, 1] est le taux de croisement.
L'ajout de la condition 0, . permet d'éviter de
créer des clones en s'assurant que les
nouvelles solutions aient au moins une composante issue du
vecteur mutant [Mathieu, 2008].
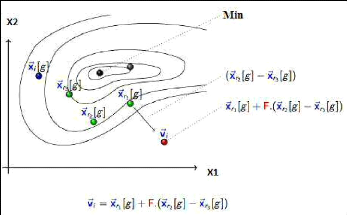
Figure 3.1 Mutation différentielle
[Dutech, 2010].
Ce croisement (développé par Stone et Price) est
appelé croisement binomial. Il existe un autre type de
croisement fréquemment utilisé dans des variantes plus
récentes de l'ED que celle de Storn et Price, c'est le croisement
exponentiel. Dans ce type de croisement, à partir d'une position
choisie aléatoirement, T composants successifs de l'individu
mutant, sont transmis à l'individu d'essai [Draa, 2011], comme le montre
la figure 3.2.
Chapitre 3 Évolution différentielle
40
2.3 Sélection
Pour la sélection, toutes les solutions dans la
population ont la même chance d'être sélectionnées
comme des parents, selon la fonction d'adaptation. La sélection entre
l'individu cible et l'individu d'essai, va décider lequel des deux
individus survivra dans la prochaine génération, selon la
qualité de leurs finesses, comme indiqué dans l'équation
suivante [Ston, price, 1997 ; Draa, 2011 ; Neggaz et Benyettou] :
X= , < ( )
> ( ) (3.3)
,
Figure 3.2 Croisement différentiel : a)
croisement binomial, b) croisement exponentiel
[Purcina, Saramago, 2008].
2.4Critère d'arrêts
Le critère d'arrêt d'un AED est
généralement l'un des suivants :
a) Temps écoulé : L'algorithme s'arrête
s'il n'y a pas un changement de la fonction fitness d'une population pour un
nombre de génération spécifié [Kajee-Bagdadi,
2007].
b) L'obtention de la qualité requise de la fonction
d'adaptation [Draa, 2011].
c) Nombre maximal de génération : L'algorithme
s'arrête quand le nombre maximal de génération est atteint
[Kajee-Bagdadi, 2007].
Chapitre 3 Évolution différentielle
Le principe général du fonctionnement d'un
algorithme à évolution différentielle est
présenté par l'algorithme suivant :
Algorithme 3.1 Évolution
différentielle (ED)
,
Début
G 1
Choisir NP, F et CR
PG initialiser la population aléatoirement
Tant que (le critère d'arrêt
n'est pas atteint) Faire Pour (chaque individu , de
PG) Faire
Choisir les parents auxiliaires , , , et
|
Créer l'individu enfant
|
,
|
en utilisant la mutation et le
|
|
Croisement différentiels
Appliquer la sélection + + Meilleur(
Fin
Pour
G G+ 1
Fin tant que Fin
|
,
, , )
|
DE/rand to best /1:
, = , + , , ) + ( 1, 2, . (3.4)
41
3. Variantes pour l'évolution
différentielle
L'algorithme à évolution différentielle
est connu sous la forme DE/x/y/z, où la variable x est
le vecteur de base pour la mutation. La sélection de ce vecteur est
purement aléatoire (rand), mais il existe également deux autres
versions permettant de favoriser le meilleur vecteur (best), (rand-to-best). La
variable y détermine le nombre de vecteurs de
différences utilisés dans la mutation de x. La variable
z est le mode de croisement utilisé, exponentiel (exp) ou
binomial (bin).
Les variantes d'AEDs diffèrent
généralement entre eux par le type de mutation utilisé qui
permet être résumés dans les équations suivants
[Ston, price, 1997 ; Neggaz et Benyettou] :
|
DE/rand/1 :
|
= 3, + 2, . (3.4)
, 1,
|
DE/best /1 : , = , + 2, . (3.4)
1,
|
DE/rand/2 :
DE/best /2 :
|
= 1, + 3, ) + ( 4, 5, . (3.4)
, 2,
= , + 2, ) + ( 3, 4, . (3.4)
, 1,
|
Chapitre 3 Évolution différentielle
Où :
,
42
: Individu de la génération courante G.
x : ensemble de population et F : constante de
mutation [0,2].
, , 1, , 2, , 3, , 4, ,, sont
aléatoirement choisis dans la génération courante.
4. Avantages et limites de l'évolution
différentielle
4.1 Avantages de l'évolution
différentielle
On peut citer les avantages d'évolution
différentielle dans les points suivants [Das et Suganthan, 2011 ; Draa,
2011 ; Karaboga, Okdem, 2004] :
- L'ED est plus simple à implémenter qu'autres
approches évolutionnaires. Pour cette raison est le plus utilisé
par les non-informaticiens.
- Trouver le minimum global réel quel que soit les
valeurs de paramètres initiales et convergence rapide.
- On peut contrôler AED sans difficultés car il
possède un nombre de paramètres de contrôles limité
(CR, F et NP dans la version de base).
- La complexité spatiale de l'ED est réduite,
quand on la compare à d'autres algorithmes performants
célèbres tels que le CMA-ES. Cette caractéristique permet
d'étendre l'ED pour résoudre des problèmes d'optimisation
de grandes dimensions.
- Malgré sa simplicité, l'évolution
différentielle offre des performances remarquablement meilleures que
celles offertes par plusieurs autres approches d'optimisation, notamment les
AEs et le PSO.
4.2 Limites de l'évolution
différentielle
Malgré son efficacité et sa robustesse, l'ED
souffre principalement des limites
suivantes [Draa, 2011] :
- Comme tous autres algorithmes d'optimisation, la performance
d'AED est très
sensibles des valeurs des paramètres F, CR
et NP.
- le choix des paramètres est très dépendant
du problème à résoudre.
- Le problème de convergence prématurée.
- Comme tout autre AE, la performance d'un AED se
détériore avec la croissance de
la dimension de l'espace de recherche.
Chapitre 3 Évolution différentielle
43
? Dans, l'évolution différentielle, le concept de
voisinage, concept clé dans les stratégies d'évolution est
manquant.
5. Conclusion
Dans ce chapitre on a présenté l'évolution
différentielle : ses principes, son comportement général,
quelques variantes de l'évolution différentielle ont
été abordées, ainsi que ses avantages et ses limites.
Dans le chapitre suivant, nous présenterons deux nouveaux
algorithmes à évolution différentielle pour le recalage
d'images, à savoir : un algorithme différentiel
linéairement adaptatif et un algorithme différentiel
périodiquement adaptatif.
| 


