Chapitre 4 :
« Savoir où l'on veut aller, c'est très
bien ; mais il faut encore montrer qu'on y va »
Emil ZOLA
1. Chapitre 4 Contributions
44
Introduction
Ce chapitre est consacré à la description de
nos deux contributions, à savoir: adaptation linéaire et
adaptation périodique des paramètres pour le recalage d'images
médicales multimodales. L'application de nos algorithmes pour
déférents types de transformations (rigide, rigide avec zoom et
affine) est décrite dans la première partie du chapitre. Dans sa
deuxième partie, le chapitre analyse et discute les différents
résultats expérimentaux.
2. Formulation de problème
Le problème traité dans ce travail peut
être formulé comme suit. Étant données deux image
I1 et I2 obtenues de capteur identiques (recalage
monomodale), ou différents (recalage multimodal), il s'agit de trouver
la transformation géométrique T qui permet d'aligner correctement
les deux images.
Les algorithmes proposés, basés sur
l'évolution différentielle, permettent d'estimer la
transformation géométrique T. Il s'agit d'une approche iconique
puisque les deux algorithmes considèrent la totalité de
l'information photométrique contenue dans les images.
Pour ce faire, on doit d'abord définir d'une
représentation des solutions adoptée, d'une mesure de
similarité qui permet une évaluation quantitative de la relation
entre deux images lors de leur superposition, et d'une stratégie de
recherche.
2.1. Représentation des individus
Formellement, les individus dans un Algorithme à
Évolution Différentielle (AED) sont représentés par
des vecteurs Narg-dimensionnels de valeurs réelles xi V i E
[1, Np] , où: Narg est le nombre des
paramètres à optimiser et Np est la taille de la
population. La longueur de chaque individu dépend du type de la
transformation recherchée.
Figure 4.1 Un individu pour une Transformation
Similitude.
Chapitre 4 Contributions
45
2.2. Espace de recherche
Nous avons appliqué notre algorithme dans les trois
transformations Suivantes.
2.2.1 Transformation rigide
Dans ce type de transformation qui est la composition d'une
translation et d'une rotation, on a trois paramètres : dx,
dy pour la translation et ? pour la rotation, la nouvelle position
(?', ?') d'un point (?2, ?2) de la deuxième image est
calcule comme suit :
?
?'_ (d?l (c??? ????) (x2) ?' -- \d?l
+ `--???? ????) `Y2) 4.1
Les paramètres dx et dy appartiennent à
l'intervalle [-20, 20] tandis que ? appartient à l'intervalle [-50, 50]
degré. Un individu encode les trois paramètres : dx, dy, ?. Donc
il s'agit alors de chercher dans l'espace R3 les valeurs des
paramètres donnant la meilleure superposition des deux images.
2.2.2 Transformation rigide avec zoom
(similitude)
Cette transformation formée par la combinaison d'une
translation, une rotation et un changement d'échelle S
(agrandissement ou réduction), la nouvelle position de chaque pixel
dans l'image résultante (?', ?') d'un point (?2, ?2) de l'image à
recaler est calcule comme suit :
?
?'\ _ (d?l (c?se
????).(x2)
?')--\"YI+S~ `--???? ????/`?2/ 4.2
Le facteur d'échelle s appartient à
l'intervalle [0, 2]. Un individu encode donc les quatre paramètres : dx,
dy, ? et S. Donc il s'agit alors de chercher dans l'espace
R4 les valeurs des paramètres donnant la meilleure
superposition des deux images.
2.2.3. Transformation affine
Pour la transformation affine, l'individu encode les six
paramètres : ??, ??, ?11 , ?12, ?21, ?22 tel que chaque point dans
l'image I2 est calculé à partir de sont correspondant
dans I1 comme suit :
|
??1 _ (d?l ?' -- \d?) + ?
|
?11
?21
|
?12)
?22/
|
(x2 `Y2?
|
4.3
|
Les paramètres ?11 , ?12, ?21, ?22 appartiennent à
l'intervalle [-2, 2].
Chapitre 4 Contributions
46
2.3. Fonction objectif
Pour l'évaluation d'une transformation, on a besoin
d'une mesure de similarité. Il existe plusieurs mesures de
similarité parmi lesquelles nous citons : le coefficient de
corrélation, le critère quadratique, la corrélation
croisée normalisée, etc. Ces mesures sont simples et facile
à programmer mais ne sont pas adaptées au cas d'un recalage multi
modale où les images ont des structures similaires mais des
caractéristiques différentes. L'information mutuelle est l'une
des mesures adaptée à la comparaison d'images multi sources. Elle
est définie par l'expression :
IM (I1, I2) = H (I1) + H (I2) - H (I1, I2)
Les entropies séparées H(I1) et H(I2) mesurent
la complexité des images I1 et I2. L'entropie jointe H (I1, I2) mesure
la quantité d'information que les images I1 et I2 apportent en
même temps. Comme nous avons dit dans le premier chapitre, L'information
mutuelle est maximale dans le cas d'une totale dépendance, et minimale
dans le cas contraire.
2.4. Stratégie de recherche
L'information mutuelle est maximale dans le cas d'une parfaite
superposition. Donc, l'idée est de définir une stratégie
de recherche ayant pour objectif de maximiser cette mesure. Le problème
revient donc à explorer l'ensemble des paramètres pour maximiser
cette mesure.
3. Contributions
L'algorithme à évolution différentiel de
base, comme déjà mentionné dans le chapitre
précédent, soufre du problème de convergence
prématurée. Par exemple, la figure 4.3 montre l'évolution
de l'information mutuelle équivalente au recalage des images de la
figure 4.2. On peut bien voir que l'algorithme de base souffre du
problème des minima locaux. Ceci est principalement causé par le
fait qu'avec le temps, les individus deviennent égaux à cause de
l'impact de l'opérateur de mutation et donc, la mutation
différentielle sera incapable de créer la diversité au
sein de la population.
Pour résoudre ce problème, on a proposé
deux nouvelles extensions de l'AED. Ces deux variantes sont nommées
respectivement : Evolution Différentielle Linéairement Adaptative
(EDLA) et Evolution Différentielle Périodiquement Adaptative
(EDPA). Dans ce qui suit, ces deux variantes seront expliquées.
Chapitre 4 Contributions
47
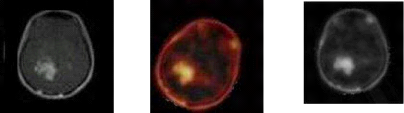
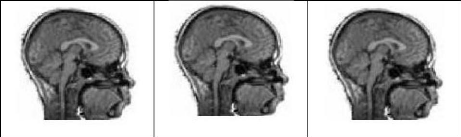
Image de référence Image d'entrée Image
Résultat
Figure 4.2 Recalage rigide multimodale.
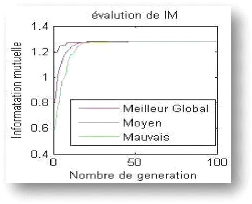
Figure 4.3 Le meilleur global, le moyen et le
minima locaux aux cours du recalage rigide des images de la figure 4.2
3.1. Evolution Différentielle Linéairement
Adaptative (EDLA)
Dans cette variante, nous avons défini les deux facteurs
de mutation (Fd) et de croisement (Fc),
généralement donnés come des constantes dans la version de
base, par les deux équations linéaires suivantes :
?
?? = ????? - ?????? - ????? ? * ??/???? = ????? + ?????? - ?????
? * ??/?? (4.1)
Où ?? ? ?????? , ????? ? = ?0.5,1? et ?? ? ?????? , ?????
? = ?0.5,1?. It : itération en cours et Ng : le nombre
maximum de générations.
Chapitre 4 Contributions
48
On voit bien de cette formule que Fd décroit avec
le temps et Fc accroît avec le temps.
3.2. Evolution différentielle
périodiquement adaptatif (EDPA)
Dans la deuxième de nos contributions, le facteur de
mutation Fd est contrôlé par l'équation
sinusoïdale suivante :
iFd = sjn(f * j) * j/Ng 4.2
Fc = 0
Où : j E{1,...... Ng}; Ng : est le
nombre maximal de génération ; et f est la
fréquence. Le signe de facteur de mutation représente la
direction de graph.
Dans cette contribution nous avons initialisé le facteur
de croisement (Fc) à la valeur 0. Puisque l'équation
périodique est capable de gérer l'équilibre entre
l'exploration et l'exploitation.
Comme le montre la figure 4.4, le facteur Fd change sa
direction d'évolution d'une façon périodique. Ce qui donne
lieu à une bonne balance entre l'exploitation et l'exploration.
L'avantage principal de cette deuxième approche est qu'on
a pu éliminer l'opérateur de croisement de l'algorithme. Donc,
une complexité algorithmique réduite est associé à
cette deuxième variante.
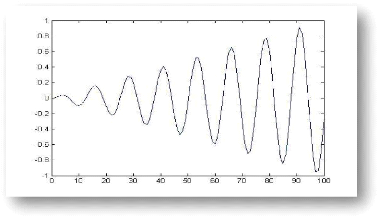
Figure 4.4 Équation sinusoïdale du
facteur Fd
Chapitre 4 Contributions
49
3.3. Résultats expérimentaux
Le but de cette section est d'évaluer les performances
des deux contributions à travers leur application sur des paires d'image
de test. Des comparaisons statistiques sont fournies pour pouvoir comparer nos
approches avec l'algorithme différentiel de base.
3.3.1. Résultats numériques
On présente ici quelques résultats
numériques pour les trois types de transformations rigide, rigide avec
zoom et affine. Pour chaque paire d'image, les algorithmes AED, EDLA et EDPA
sont exécutés 30 fois pour les deux premiers types de recalage et
5 fois pour le cas du recalage affine (car plus de temps de calcul est
nécessaire pour ce dernier). On donne la moyenne (moy),
l'écart type (STD) et le médian (médian)
de la valeur de l'information mutuelle sur l'ensemble des 30 exécutions
ainsi que la meilleure (meilleurIM) et la mauvaise (mauvaisIM) valeur de
l'information mutuelle. Ces résultats sont présentés dans
le tableau 4.1.
? Le choix des paramètres :
Dans l'algorithme de base, Nous avons fixé le facteur
de mutation Fd par la valeur 0.6301 et le facteur de croisement Fc
par la valeur 0.7122. Ces valeurs sont tirées de la
littérature, à base de travaux actant sur le réglage de
paramètres de l'ED de base.
Nous avons utilisé une population (Np) de 20
individus, ces individus sont représentés par des vecteurs de 3,
4 et 6 variables réelles (pour différents types de
transformation). Le nombre d'itérations a été choisi
d'être 20, 50 et 100 pour le recalage rigide, la similitude et l'affine
respectivement.
Les valeurs des paramètres propres aux contributions
sont fixées empiriquement comme suit. Dans la première variante,
EDLA, les bornes supérieures et inférieure des valeurs de Fd
et de l'Fc sont égales à 0.9 et 0.4 respectivement.
Dans la deuxième variante, la fréquence f de
l'équation sinusoïdale est choisie d'être égale
à 1/5.
50
Chapitre 4 Contributions
|
Paire
d'images
|
AED
|
EDLA
|
EDPA
|
|
Moy
|
STD
|
Médian
|
Moy
|
STD
|
Médian
|
Moy
|
STD
|
Médian
|
|
MeilleurIM
|
MeilleurIM
|
MeilleurIM
|
|
MauvaiseIM
|
MauvaiseIM
|
MauvaiseIM
|
|
PI1
|
1.1174
|
0.1043
|
1.1530
1.2169
0.8621
|
1.2777
|
3.4510e-004
|
1.2777
1.2782
1.2771
|
1.2762
|
0.0012
|
1.2765
1.2777
1.2744
|
|
PI2
|
0.9031
|
0
|
0.9031
0.9031
0.9031
|
1.1474
|
0.1581
|
1.2235
1.2360
0.7873
|
0.9480
|
0.0516
|
0.9360
1.0897
0.8772
|
|
PI3
|
1.0142
|
0.0279
|
1.0140
1.0496
0.9718
|
0.5220
|
0.2614
|
0.3536
0.9807
0.4573
|
0.7054
|
0.0974
|
0.7160
0.8542
0.6108
|
Tableau 4. 1 : Résultats
numériques des transformations : rigide et rigide avec zoom et
affine.
Le tableau 4.1 montre bien que les deux nouveaux Algorithmes
EDLA et EDPA ont presque la même performance et donnent dans la
majorité des cas (transformations rigide et similitude) de meilleurs
résultats par rapport à l'ED de base. Aussi, on a gagné un
opérateur dans la deuxième variante, EDPA ; et donc moins de
temps de calcul sera nécessaire avec des performances similaires ou
meilleures que l'algorithme de base.
3.3.2 Analyse qualitative des
résultats
Dans cette section nous donnons quelques résultats
qualitatifs des différentes approches.
a. Recalage rigide
Les figures 4.5 et 4.6 représentent respectivement, une
paire d'images à être recalée et les résultats
d'application des différentes variantes sur cette paire d'images dans le
cas rigide.
Chapitre 4 Contributions

Image référence
Image d'entrée
Figure 4.5 Paire d'image : IRM-Tomographie
calculée à rayon X(CTI).
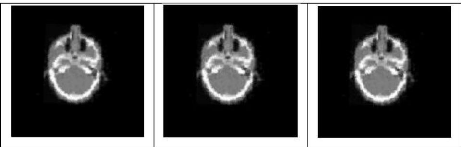
ADE : IM final : 1.037
EDLA : IM final: 1.034
EDPA : IM final: 1.037
51
Figure 4.6 Recalage rigide des images de la
figure 4.5 par ADE (à gauche), (au milieu) EDLA et
EDPA (à droite).
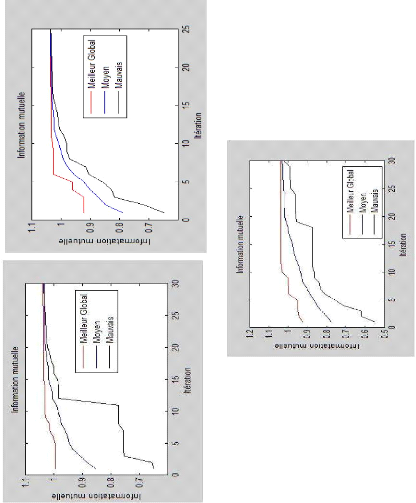
D'une autre part, les graphes de la figure 4.7 présente
à quel point les deux variantes proposées dans ce travail sont
capable d'offrir un bon compromis entre exploration et exploitation. Il est
claire des graphes de cette figure que la troisième approche est
meilleure dans sa recherche des solutions : elle permet au même temps une
bonne exploration de l'espace de recherche, et une préservation de la
diversité de la population.
Chapitre 4 Contributions
Figure 4.7 les graphes d'IM correspondant aux
images de la figure 4.6 : EDA (à gauche au-dessus), EDLA (à
droite au-dessus) et EDPL (milieu au-dessous)
52
Chapitre 4 Contributions
b. Recalage rigide avec zoom
Les figures 4.8 et 4.9 représentent respectivement, une
paire d'images à être recalée et les résultats
d'application des différentes variantes sur cette paire d'images dans le
cas de similitude. Une autre fois, la figure 4.10 montre la
supériorité de la deuxième variante en termes de garantie
du bon équilibre entre exploitation et exploration.
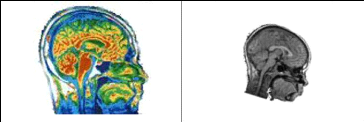
Image référence
Image recalé
Figure 4.8 : Paire d'image à recaler :
à gauche IRM coloré et à droite Scanner.
ADE : IM final : 1.3256
EDLA: IM final : 1,3268
EDPA : IM final : 1.3230
53
Figure 4.9 Recalage rigide avec zoom des
images de la figure 4.8.
Chapitre 4 Contributions
54
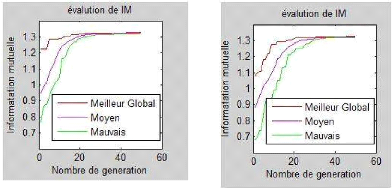
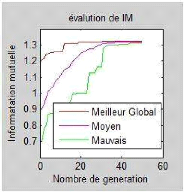
Figure 4.10 les graphes d'IM correspondant aux
images de la figure 4.9: EDB (à gauche au-dessus),
EDLA (à
droite au-dessus) et EDPL (milieu au-dessous).
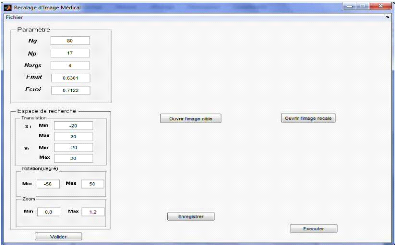
5. Interface Graphique
Une interface graphique permettant de faciliter la tâche
de réglage de paramètres au médecin, qui n'est pas
familier avec l'outil de développement (Matlab dans ce travail), a
été développée. Cette interface permet :
l'accès aux de images à être recalée, le
réglage des paramètres et le lancement de la recherche de la
meilleure transformation. Les figures 4.11 et 4.12 représente
respectivement l'interface graphique de l'application avant et après
exécution de l'algorithme en question.
Chapitre 4 Contributions
55
Figure 4.11 : Interface de transformation
similitude avant l'exécution.
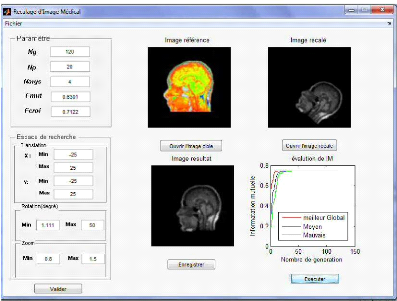
Figure 4.12 : Interface de transformation
similitude après l'exécution.
Chapitre 4 Contributions
56
6. Conclusion
Dans ce chapitre deux nouvelles variantes de l'algorithme
à évolution différentielle pour le recalage d'images
médicales multimodales ont été proposées. Dans la
première variante, une adaptation linéaire du facteur de mutation
et de la probabilité de croisement est adoptée. Dans la
deuxième, on a utilisé une adaptation sinusoïdale du facteur
de mutation, et on n'a pas appliqué le croisement, car la mutation par
facteur d'amplification périodiquement adapté a permis d'assurer
le bon équilibre entre exploitation et exploration. Ceci a donné
lieu à une complexité algorithmique relativement
réduite.
Dans l'ensemble, les résultats expérimentaux ont
montré que les deux approches proposées sont meilleures ou au
moins concurrentes à l'évolution différentielle de base
dans le cas du recalage d'images médicales multimodales.
57
| 


