A.3.5.Croisement
Pour enrichir la diversité de la population il faut
faire un croisement, car s'il n y a pas de croisement les enfants sont
exactement des copies de leurs parents. L'operateur de croisement se
déroule en trois étapes : au début il faut faire un choix
aléatoire de deux parents et on choisir un ou plusieurs points de
croisements, ensuite on échange les valeurs des deux parents par rapport
de ce point de croisement. Il existe plusieurs types de croisement à
point, à 2point ou à plusieurs points.
A.3.6.Mutation
L'operateur de mutation consiste à modifier
aléatoirement avec une certaine probabilité la valeur d'un
gène à partir d'une seule chaîne initiale, cet
opérateur garantit la diversité de la population. On distingue
plusieurs types de mutation selon le type de codage utilisé, dans le
codage binaire il consiste simplement à changer un 0 en un 1 ou
l'inverse. La probabilité Pm de mutation est
généralement choisi très faible (?comprise entre 0.01 et
0.001) [Souquet et Radet, 2004].
A.3.7.Remplacement
Cet opérateur est basé, comme l'opérateur
de sélection, sur la fitness des individus. Son rôle consiste
à déterminer les chromosomes parmi la population courante
constituant la population de la génération suivante. Cette
opération est appliquée après l'application successive des
opérateurs de sélection, de croisement et de mutation. On trouve
essentiellement 2 méthodes de remplacement différentes : Le
remplacement stationnaire et le remplacement élitiste.
A.4.Critères d'arrêts
Pour arrêter l'algorithme génétique il ya
plusieurs critères d'arrêt sont possibles. On peut arrêter
l'algorithme s'il n'y a pas un changement de la fonction de fitness d'une
population pour un nombre de génération spécifié.
On peut aussi arrêter l'algorithme lorsque le nombre de
génération est atteint ou lorsque le temps spécifique
s'écoule.
Chapitre 02 Métaheuristique d'optimisation
31
Chapitre 02 Métaheuristique d'optimisation
A.5.Avantages et désavantages d'AG
a) Avantages d'AG
On peut citer les avantages d'AGs dans les points suivants
[Moutairou, 2009 ; Whitley, 1994 ; Yoon et al., 1994 ; Draa, 2011]:
- Il fait un bon équilibre entre l'exploration et
l'exploitation de l'espace de recherche. - La recherche de l'optimum est
globale.
b) Désavantages d'AG
On peut citer les limites d'AGs dans les points suivants
[Moutairou, 2009 ; Whitley, 1994 ; Yoon et al., 1994 ; Draa, 2011]
:
- Les algorithmes génétiques convergent
rapidement vers une solution locale dans les premiers stades, mais la
convergence vers une solution optimale peut nécessiter plus de temps.
- La qualité des résultats obtenus est
tributaire de l'ajustement des paramètres de l'algorithme (à
savoir, les probabilités de croisement et de mutation) qui est souvent
empirique.
B. Évolution Différentielle
L'évolution différentielle est un algorithme
développé par Storn et Price en 1995, qui est basé sur
population. Il utilise les mêmes opérateurs de l'algorithme
génétique : croisement, mutation et sélection, car il est
inspiré par ces algorithmes, mais il basé sur une nouvelle
stratégie de mutation. Dans le chapitre suivant nous essayerons
d'étudier cet algorithme en détail, car c'est le noyau de notre
approche pour le recalage.
4.1.2. Optimisation par essaim de
particules
L'optimisation par essaim de particules (en Anglais Particle
Swarm Optimization PSO) est une technique d'optimisation globale
stochastique développée par Eberhart et Kennedy en 1995 [Kennedy
et al., 1995], qui utilise une population de solutions potentielles
(particules) pour développer une solution optimale au problème.
Le degré d'optimalité est mesuré par une fonction fitness
(aptitude) définie par l'utilisateur. Cette technique est
inspirée par le comportement social des essaims d'oiseaux, ces animaux
caractérisent par le concept
32
d'intelligence commune où chaque particule ne
possède qu'une information partielle de son environnement qui
collectivement permet de gérer intelligemment le groupe [Barrette,
2008].
Les particules sont les individus et elles se déplacent
dans l'hyperespace de recherche. Le processus de recherche est basé sur
deux règles [Dutot, Olivier] :
1. Chaque particule est dotée d'une mémoire qui
lui permet de mémoriser le meilleur point par lequel elle est
déjà passée et elle à tendance à retourner
vers ce point.
2. Chaque particule est informée du meilleur point connu
au sein de son voisinage et elle va tendre à aller vers ce point.
? Modèle d'optimisation par essaim de particules
de base
L'essaim se compose d'un certain nombre de particules qui se
déplacent dans l'espace de recherche, chaque particule p
possède deux variables d'état où : x(t) est
la position courante et v(t) est la vitesse courante, il
possède aussi une petite mémoire où : p(t) est la
meilleure position précédente, et g(t)est la meilleure
p(t) de toutes les p?N(p) [Chikhi,
2010].
Les expressions suivantes pour les positions et les vitesses
des particules dans le prochain pas de temps sont données par ces
équations récursives :
|
#177; 1
|
=
|
#177;
|
1 #177; 2
|
2.1
|
|
#177; 1
|
=
|
#177;
|
#177; 1
|
2.2
|
Où , qui limite chaque coordonnée de v(t)
à V= [-vmax, vmax] et
C1, C2 qui
déterminent
l'influence de p(t) et g(t) dans la formule de
mise à jour de vitesse [Chikhi, 2010].
L'algorithme de PSO possède plusieurs avantages. En
effet, est un algorithme simple a implémenter, très efficace dans
la recherche global, facile à paralléliser pour le traitement
concurrent et enfin il possède très peu de paramètres
à régler. Cependant, il possède certaines limites comme le
taux de convergence lente à l'étape de la recherche locale
[Nebti, 2005], et le problème de convergence prématurée
dans le cas où le taux de convergence est rapide.
4.1.3. Optimisation par les colonies de
fourmis
L'optimisation par colonie de fourmis est une technique
d'optimisation basée sur la population. Elle a été
introduite pour la première fois par Dorigo. Les algorithmes de
colonies de fourmis sont nés d'une constatation simple : les insectes
sociaux, et en particulier les fourmis, résolvent naturellement des
problèmes complexes. Un tel comportement est possible
Chapitre 02 Métaheuristique d'optimisation
car les fourmis communiquent entre elles de manière
indirecte par le dépôt de substances chimiques, appelées
phéromones, sur le sol. Ce type de communication indirecte est
appelé stigmergie1 [Cooren, 2008].
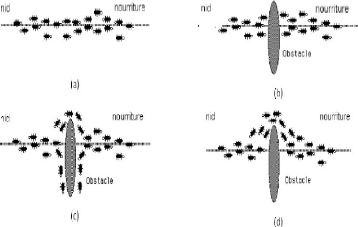
La principale illustration de ce constat est donnée par
la « Figure 2.14 ». On voit sur cette Figure que, si un obstacle est
introduit sur le chemin des fourmis, les fourmis vont, après une phase
de recherche, avoir tendance à toutes emprunter le plus court chemin
entre le nid et l'obstacle. Plus le taux de phéromone à un
endroit donné est important, plus une fourmi va avoir tendance à
être attirée par cette zone. Les fourmis qui sont arrivées
le plus rapidement au nid en passant par la source de nourriture sont celles
qui ont emprunté la branche la plus courte du trajet. Il en
découle donc que la quantité de phéromones sur ce trajet
est plus importante que sur le trajet plus long.
Ces algorithmes utilisés pour résoudre plusieurs
problèmes comme le problème de voyageurs de commerce.
33
Figure 2.5 Détermination du plus court
chemin par une colonie de fourmis. (a) Situation initiale, (b) Introduction
d'un obstacle, (c) Recherche du chemin optimal, (d) Prédominance du
chemin optimal.
1Interactions sociales indirectes
Chapitre 02 Métaheuristique d'optimisation
34
Chapitre 02 Métaheuristique d'optimisation
35
Algorithme 2.2 : optimisation par colonies de
fourmis
Début
Initialiser les traces à 0 pour toute décision
possible d
Tant qu'aucun critère
d'arrêt n'est satisfait faire
Construire AI solutions en tenant compte de la force gloutonne et
de la trace
Mettre à jour les traces ainsi que la meilleure solution
rencontrée;
Fin tant que
Fin
4.2.Métaheuristique a base de
voisinage
Les méthodes à base de voisinage (ou
méthodes de recherche locale) sont des méthodes qui travaillent
sur un seul point de l'espace de recherche à un instant donné.
4.2.1. Recuit simulé
La méthode du Recuit Simulé (RS) a
été proposée par des chercheurs d'IBM en 1983 [KIR, 83],
cette méthode est une technique de recherche locale fondée sur
une analogie entre un processus physique (recuit) et le problème
d'optimisation. Cette méthode en tant que métaheuristique
s'appuie en effet sur des travaux visant a simulé l'évolution
d'un solide vers son état d'énergie minimale.
Le recuit simulé s'appuie sur l'algorithme de
Métropolis-Hastings, qui permet de décrire l'évolution
d'un système thermodynamique. Par analogie avec le processus physique,
la fonction à minimiser deviendra l'énergie E du
système. On introduit également un paramètre fictif, la
température T du système.
L'algorithme du recuit simulé part d'une solution
donnée, et la modifie itérativement jusqu' à le
refroidissement du système. Les solutions trouvées peuvent
améliorer le critère que l'on cherche à optimiser, on dit
alors qu'on a fait baisser l'énergie du système, comme elles
peuvent les dégrader. Si on accepte une solution améliorant le
critère, on tend ainsi à chercher l'optimum dans le voisinage de
la solution de départ [Layeb, 2010].
La méthode du Recuit Simulé possède
plusieurs avantages, c'est une méthode générale et facile
à programmer et se produit des solutions de bonne qualité, mais
elle peut présenter quelque limite comme le problème de temps de
calcul excessif dans certaines applications et le nombre important de
paramètres à ajuster [Saha, 2010].
Algorithme 2.3Optimisation par le recuit
simulé
Début
Déterminé une configuration aléatoire
S
Choix des mécanismes de perturbation d'une
configuration
Initialiser la température T
Tant que la condition d'arrêt
n'est pas atteinte faire
Tant que là l'équilibre
n'est pas atteint faire
Tirer une nouvelle configuration S'
Appliquer les règles de metropolis
Si f(S') < f(S)
Smin = S'
fmin = f(S')
Fin Si
Fin Tant que
Décroitre la température
Fin Tant que
Fin
4.2.2. Recherche Tabou
La recherche tabou est une métaheuristique de recherche
locale a été présentée par Fred Glover en 1986,
l'idée est de passe d'une solution valide a une autre les deux solutions
sont dites alors voisines. L'ensemble des solutions que l'on peut atteindre
à partir d'une solution s'appellera alors un voisinage.
On commence par l'initialisation d'un liste vide de longueur
maximale, cette liste contiendra tous les mouvements que l'on a
déjà effectué et deviennent donc interdits, cette
méthode permet d'éviter de tomber dans un cycle de mouvement
répétitives, donc à chaque itération, on va choisir
le meilleur mouvement possible dans le voisinage de la solution actuelle sans
faire de mouvement contenus dans la liste tabou «liste de mouvements
interdits».
Dans sa forme de base, l'algorithme de recherche tabou
présente l'avantage de comporter moins de paramètres que
l'algorithme de recuit simulé. Cependant, l'algorithme n'étant
pas toujours performant, il est souvent approprié de lui ajouter des
processus d'intensification et/ou de diversification, qui introduisent de
nouveaux paramètres de contrôle [Glover et al., 1997 ; Cooren,
2008]. L'algorithme général de la recherche tabou est le suivant
[Rodriguez-Tello et al, 2005] :
Chapitre 02 Métaheuristique d'optimisation
Algorithme 2.4Optimisation par la recherche
tabou
Début
S = solution initiate
Best = S
Répéter
Sbest = meilleur voisin de S
si(fitness(Sbest) < fitness (Best))
Alors
Best = Sbest
Mise à jour de la liste Tabou
S = Sbest ;
Jusqu'à(critère de fin est
vérifié)
Retourner Best ;
Fin
4.2.3. Méthode de la Descente
(Hill-Climbing)
Cette méthode est très simple et ancien, elle
procède de manière itérative, en choisissant à
chaque itération un point dans le voisinage de la solution courante.
S'il est meilleur c'est à dire il améliore la solution courante,
il devient la nouvelle solution courante, sinon un autre point est choisi, et
ainsi de suite c'est à dire que ce procédé est
répété aussi long temps que la valeur de la fonction
objectif diminue. La recherche s'interrompe des lors qu'un minimum local de
f est atteint [Troudi, 2006].
La méthode de Hill climbing possède plusieurs
avantages, c'est une méthode intuitive et simple mais
présenté aussi quelque limite comme le problème de minimum
local et la lenteur de la méthode [Layeb, 2010].
Algorithme 2.5 : Optimisation par la
méthode de descente
Début
Générer et évaluer une solution initiale
s
Tant que La condition d'arrêt n'est
pas vérifiée faire
Modifier s pour obtenir s' et évaluer s'
Si (s'est meilleure que s) alors
Remplacer s par s'
Fin si
Fin tant que
Retourner s
Fin
36
Chapitre 02 Métaheuristique d'optimisation
37
4.3 Méthodes hybrides
Une autre façon d'améliorer les performances
d'un algorithme ou de combler certaines de ses lacunes consiste à le
combiner avec une autre heuristique [Talbi, 2000 ; Benlahrache, 2007]. Les
algorithmes hybrides sont considérés parmi les méthodes
les plus puissantes pour résoudre les problèmes d'optimisation.
Cette puissance réside dans la combinaison des deux principes de
recherche de meilleure solution, fondamentalement différents. Il existe
plusieurs types d'hybridation parmi eux, on peut citer: l'hybridation entre les
méthodes de recherche globale et locale, l'hybridation entre les
métaheuristiques et les méthodes exactes et l'exécution en
parallèle qui consiste à lancer en parallèle
l'exécution de la même métaheuristique.
5. Conclusion
Dans ce chapitre nous avons présenté des
méthodes approchées utilisées pour la résolution de
problèmes d'optimisations connues sous le titre de
métaheuristique. Les métaheuristiques sont des méthodes
stochastiques qui visent à résoudre un large panel de
problèmes, le but visé par ces méthodes est d'explorer
l'espace de recherche efficacement afin de déterminer des solutions
(presque) optimales, elles ont rencontrées un vif succès
grâce à leur simplicité d'emploi mais aussi à leur
forte modularité. Malgré les bons effets des
métaheuristiques, elles peuvent donner de mauvais résultats.
La performance d'une métaheuristique dépend de
plusieurs facteurs. La limite majeure de métaheuristique dépend
du paramétrage, car il existe très peu de règles
universelles permettant de connaître le paramétrage idéal
et généralement, seules l'expertise et l'expérience de
l'utilisateur permettront de faire un choix.
Dans le chapitre suivant, nous présentons une
méthode basée-population appelée algorithmes à
évolution différentielle (ED). C'est cette approche qu'on va
étendre pour la résolution du problème de recalage
d'images médicales.
| 


