2.4 Entanglement
We describe that quantum mechanics include states but those
states are characterized in two [Sar], pure and mixed state which are
define by any linear operator acting on H called density
operator, satisfies the following properties:
1. ñ is define positive ñ 0;
2. tr(ñ) = 1
For the following conditions, we describe other conditions for
a state. Pure state are define when ñ2 =
ñ and ñ2 > ñ. i.e
when we have a pure state we have always an unique state vector. In the hilbert
space it is expressed as a projection operator on |ø). For the
mixed state, the definition is quite different than the pure state. The mixed
state is a combination of pure states. Entanglement notion is defined as an
inseparable state in quantum mechanics, it can be taken as two states which are
commited that means [A,B] = 0. In more details, let's consider
corresponding Hilbert spaces on the state A and B where we write respectively
HA and HB. The composite system is a product
HA®HB. If the first can be represented by
|ø)A and the second by |ø)B,
the product is given by |ø)A ®
|ø)B. Those states in binary notation will take
|ø)A = {|0)A, |1)A} and
|ø)B = {|0)B, |1)B}, thus
the basical representation
Section 2.5. No-cloning Theorem Page 12
of entanglement using binary representation is:
v2
1
v2
1 (|0iA|0iB + |1iA|1iB); (2.4.1)
(|0iA|0iB - |1iA|1iB). (2.4.2)

)
| ?i|?i - |?i|?i
(2.4.7)
The quantization notation is what we will use more in the next
point where we will go through and more details in quantum protocols.
2.5 No-cloning Theorem
With those main values which is differenciate by a sign, the bits
can be shift to get a four maximal
entaglement states otherwise we get the Bell basis,
1
|ö+i = v2(|00i + |11i, (2.4.3)
1
|ø+i = v2(|01i + |10i, (2.4.4)
1
|ö-i = v2(|00i - |11i), (2.4.5)
1
|ø-i = v2(|01i - |10i). (2.4.6)
Bell said : The
probabilities of outcomes of the measurements of certain quantum-mechanical
observables on one system are not immediately influenced by the kinds of
measurements directly made on a second system, which is sufficiently spatially
separated from the first. Choosen a quantization axis, the entanglement state
is given with spins up or down example
1
|ø-i =
v2(
Having a classical information, we can share it to differents
entities without any problem. We can duplicate the information. But in quantum
information such operation seems quite impossible. In 1982, Wootters, Zurek and
Deiks stated a no-cloning theorem which profound an implication in quantum
computing and its related field [NAZ02] of quantum cryptography. With a quantum
state choosen from a given set of possible states can be cloned perfectly only
if the states in the set that are mutually orthogonal. But if a set of states
is orthogonal, the states are related to each other in the same way that
classical alternatives are related to each other. There is none of the
ambiguity that typically charactarizes the relation among quantum states. This
is what we meant when we said cloning is possible only if the information being
cloned is essentially classical. More explaination can be found [NAZ02]
2.5.1 Characteristics of no-cloning theorem.
After many experience, the following characteristics come up to make a
point in the security of the message without using a error
/The no-cloning theorem use to prevents using a classical
error technic on quantum states.(Enable to create a backup copies of states
)
/The quantum measurement is impossible. That means the state
in quantum area can not be diplucate. /The no-cloning theorem does not prevent
superluminal communication via quantum entanglement, as cloning is a sufficient
condition for such communication, but not a necessary one.
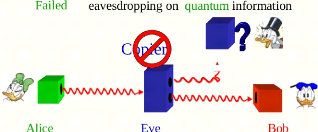
Section 2.5. No-cloning Theorem Page 13
Figure 2.4: No-cloning
14
| 


