Quantum key distribution theory and practice

2.1 Polarization

First, we will present the polarization of a classical electromagnetic field and translate it in the frame of quantum mechanics. According to Maxwell's equations in the vacum, we observed that light is a transverse electromagnetic wave which means that the electromagnetic field is perpendicular to the direction of propagation of the wave. To simplify, we will consider a monocromatic wave which propagates along the z-axis :

E~ = ^~E_ocos(ùt - kz + ?), (2.1.1)

Section 2.2. Circular polarization Page 9

E_x =

Eo _v2coswt; (2.2.1)

2r

where w is a vibration frequency, |E_o| is the amplitude, k is the wave vector given by k = À , and À

is the wavelenght. The vibration frequency is given with the relation

w = c x k, (2.1.2)

here c is the speed of light and ? is the phase at the origine. The electomagnetic field is polarized in the plane perpendicular to the direction of propagation thus we let z = 0.

2.1.1 Linear polarization. In the linear polarization, the electric field describe a straight line in a single direction which is the direction of propagation. The mathematical relation is given by:

E_x = E0cosOcoswt, (2.1.3)

E_y = E0sinOcoswt. (2.1.4)

With Malus law, in the output of the polarization, the electric field is proportionnal to the square of the intensity.

I' = Icos²(O - á). (2.1.5)

If O = á - ð 2 that imply in the output of the analyzer, we will not get any light.

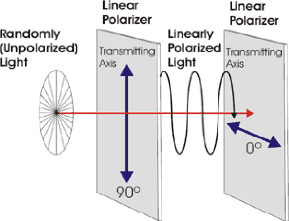
Figure 2.1: Linear polarization

The orientation of a linearly polarized electromagnetic wave is defined by the direction of the electric field vector

2.2 Circular polarization

The second polarization is circular, when the electric field describes a circle in the plane during the propagation of the wave along z. The wave is polarized circularly if

Section 2.3. Heisenberg Uncertainty principle Page 10

E_o

E_y =

Section 2.4. Entanglement Page 11

_v2 sinùt. (2.2.2)

This is a general cas of polarization, where the polarization of electromagnetic radiation such that the

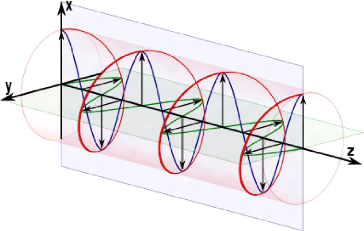
Figure 2.2: Circular polarization

tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to the direction of propagation. The mathematical definition is

ÇA cos ùt )

Ê= ;
B sin ùt

with A =6 B and A, B =6 0. satisfy to

_{ÇX )2 ÇY )2}

+ = 1. (2.2.3)

A B

2.3 Heisenberg Uncertainty principle

People are interrested in quantum mechanics such that they made many research, experiences and found new concepts which clarify the theory of quantum. In 1927, Werner Heisenberg discovered Heisenberg Uncertainty Principle. Quantum system is a system which calls mesure, hermitian operators, and observable, as define previously. Quantum mechanics is applied to the microscopic domain of particle and its the principle for complementarity [NAZ02] of two states, momentum and position. In general, Heisenberg Uncertainty Principle is given by any hermitian operators denoted by x and p, where x describes the position and p the momentum of particle in certain coordonate. This principle simutaneously increase the position and the momentum, it is impossible to measure a position without disturbing momentum, and vice versa. This principle can be called a principle of complementarity [NAZ02]; when the momentum is increased, the position decreases and when the position increase the

momentun decreass (distribution is proportionnal). In general, the Heisenberg Uncertainty Principle is given by the following formula:

~

ÄxÄp_x = ₂. (2.3.1)

Note that Ä symbol is what we call Uncertainty. The uncertainty principle is taken as a limitation of quantum preparation (states)[BHL07]. There are many application on it such that in signal processing with Fourrier transformation but the one domain that is interesting to us is cryptography. We will see how this notion is applied in cryptography. In this figure the uncertainty momentum is given by Äv is

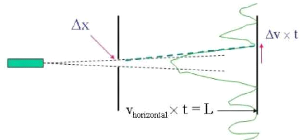
Figure 2.3: Heisenberg Uncertainty Principle

still the same as Äp.