3.5. Processus d'analyse des données
Après avoir collecté les données selon
les méthodes prescrites ci-haut dans la section 3.4, il a
été procédé avant l'analyse à une
codification qui a été suivie de la saisie en Excel. Apres la
saisie des données en Excel nous les avons transféré en
Software Package for Social Sciences (SPSS) pour une analyse approfondie.
L'analyse a plus utilisé la technique de statistique
dénommée `Khi carré' en vue de dégager la
dépendante de variable rentabilité vis- à- vis de la
variable indépendante le marketing-mix. C'est dans ce cadre que les
tableaux croisés ont été établie en vue de bien
comprendre l'influence des certains éléments sur les autres.
Nous avons aussi utilisé la technique de
régression pour vérifier les effets du marketing-mix sur la
rentabilité de la Compagnie de Valorisation Industrielle de la Banane au
Rwanda (COVIBAR).
3.6. Description de la régression et de
Khi-carré
La régression, cette technique nous a permis d'exprimer
le degré de causalité entre la variable dépendante qui est
la rentabilité et la variable indépendante qui est le
marketing-mix.
Khi-carré, cette technique nous a aidé à
apprécier le degré de la relation de la dépendance entre
la rentabilité et les variables du marketing-mix.
3.6.1. Modèle de régression et
équation de la régression
Dans cette section nous présentons le modèle de
régression linéaire simple. Dans la régression
linéaire simple, l'analyse des données bi variées
nécessite la mesure de 2 variables pour chaque échantillon. Dans
notre étude nous avons désigné par y la variable
dépendante (ou variable expliquée) et par x la variable
indépendante (ou explicative)
3.6.1.1. Modèle de régression
linéaire simple
 (1) (1)
Où  et et 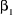 sont des paramètres du modèle, sont des paramètres du modèle,  est le point en lequel la droite coupe l'axe OY ou l'ordonnée
à l'origine est le point en lequel la droite coupe l'axe OY ou l'ordonnée
à l'origine
 : est le terme erreur qui prend en compte la variabilité de y qui
n'est pas expliquée par la relation linéaire entre x et y. : est le terme erreur qui prend en compte la variabilité de y qui
n'est pas expliquée par la relation linéaire entre x et y.
3.6.1.2. Equation de la régression
linéaire
E ( )= 0 (2), E : espérance mathématique )= 0 (2), E : espérance mathématique
E(y) = 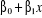 (3) appelée `équation de la régression
linéaire ' (3) appelée `équation de la régression
linéaire '
Si on a  >0 on dit que la relation linéaire entre x et y est
positive >0 on dit que la relation linéaire entre x et y est
positive
Si on a  <0 on dit que la relation linéaire entre x et y est
négative <0 on dit que la relation linéaire entre x et y est
négative
Si on a  = 0 on dit que pas de relation = 0 on dit que pas de relation
3.6.1.3. Equation estimée de la
régression linéaire simple
En pratique, puisqu'on ne connaît pas  et et  on fait recours à l'estimation tout en utilisant les
statistiques b0 et b1 de l'échantillon on fait recours à l'estimation tout en utilisant les
statistiques b0 et b1 de l'échantillon
L'équation (3) peut s'écrire sous la forme
 (4) est appelée ` Equation estimée de la
régression linéaire simple ' (4) est appelée ` Equation estimée de la
régression linéaire simple '
Ou b0 et b1 nous permettent d'estimer
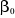 et et  respectivement respectivement
| 


