2.2 Analyse en composantes principales (ACP) et
classification des
banques de la CEMAC
L'analyse en composantes principales est une
méthode d'analyse des données appliquée sur un tableau
rectangulaire individus-variables où N individus sont décrits par
P variables quantitatives. Elle a pour but d'obtenir un résumé
synthétique des informations contenues dans le tableau de
données. Elle permet ainsi d'analyser les proximités entre les
individus, les corrélations entre les variables, les individus et les
variables simultanément.
Notre objectif dans cette analyse est de pouvoir
regrouper les banques qui ont eu des performances similaires durant toute la
période de l'étude. Nous disposons ainsi d'un tableau
rectangulaire21 comportant 24 banques décrites chacune par 48
scores mensuels sur toute la période de l'étude. Les moyennes
mensuelles des scores pour tout l'échantillon sur toute la
période de l'étude sont consignées dans le tableau
ci-dessous.
Tableau 3.6 : Moyennes mensuelles des scores de
l'échantillon
|
Janv
01
|
Févr
01
|
Mars
01
|
Avr
01
|
Mai
01
|
Juin
01
|
juil-
01
|
Août
01
|
Sept
01
|
Oct
01
|
Nov
01
|
Déc
01
|
|
0,716
|
0,660
|
0,687
|
0,718
|
0,704
|
0,714
|
0,695
|
0,695
|
0,700
|
0,672
|
0,657
|
0,693
|
|
Janv
02
|
Févr
02
|
Mars
02
|
Avr
02
|
Mai
02
|
Juin
02
|
juil-
02
|
Août
02
|
Sept
02
|
Oct
02
|
Nov
02
|
Déc
02
|
|
0,660
|
0,718
|
0,665
|
0,496
|
0,753
|
0,739
|
0,736
|
0,722
|
0,730
|
0,704
|
0,703
|
0,770
|
|
Janv
03
|
Févr
03
|
Mars
03
|
Avr
03
|
Mai
03
|
Juin
03
|
juil-
03
|
Août
03
|
Sept
03
|
Oct
03
|
Nov
03
|
Déc
03
|
|
0,684
|
0,669
|
0,661
|
0,669
|
0,605
|
0,679
|
0,685
|
0,692
|
0,444
|
0,654
|
0,729
|
0,715
|
|
Janv
04
|
Févr
04
|
Mars
04
|
Avr
04
|
Mai
04
|
Juin
04
|
juil-
04
|
Août
04
|
Sept
04
|
Oct
04
|
Nov
04
|
Déc
04
|
|
0,688
|
0,771
|
0,706
|
0,693
|
0,714
|
0,711
|
0,724
|
0,693
|
0,721
|
0,728
|
0,720
|
0,803
|
Source : COBAC, nos calculs
L'application d'une ACP normée à notre
tableau rectangulaire sous le logiciel SPAD nous a permis d'obtenir les
résultats suivants :
21 Voire annexe
Mémoire rédigé et soutenu par
Leonnel DIMOU KWAYEP 50
Tableau 3.7 : Tableau des valeurs
propres
|
Mois
|
Numéro
|
Valeur
Propre
|
Pourcentage
|
Pourcentage
cumulé
|
|
Janvier
|
1
|
27,71
|
57,74
|
57,74
|
|
Février
|
2
|
5,93
|
12,36
|
70,10
|
|
Mars
|
3
|
3,38
|
7,06
|
77,16
|
|
Avril
|
4
|
1,86
|
3,88
|
81,04
|
|
Mai
|
5
|
1,58
|
3,29
|
84,.33
|
|
Juin
|
6
|
1,23
|
2,58
|
86,91
|
|
Juillet
|
7
|
1,10
|
2,31
|
89,22
|
|
Août
|
8
|
0,97
|
2,04
|
91,26
|
|
Septembre
|
9
|
0,92
|
1,92
|
93,18
|
|
Octobre
|
10
|
0,74
|
1,54
|
94,72
|
|
Novembre
|
11
|
0,57
|
1,19
|
95,91
|
|
Décembre
|
12
|
0,40
|
0,83
|
96,75
|
Source : COBAC, nos calculs
L'inertie totale du nuage des individus et des
variables dans une ACP normée est égale au nombre de variables
actives (48 dans notre cas). L'examen du tableau des valeurs propres cidessus
permet de constater que le premier axe factoriel avec une inertie de 27,71
explique 57,74 % de l'inertie totale du nuage. Le deuxième axe quant
à lui n'explique que 12,36 % de l'inertie du nuage. Les deux premiers
axes factoriels expliquent ainsi à eux seul 70,10 % de l'inertie totale
du nuage. Nous pensons que ce pourcentage d'inertie cumulée est
satisfaisant pour pouvoir mener nos interprétations à partir des
deux premiers axes factoriels. D'autre part, si chacune des 24 banques
contribuait à part égale à la détermination des
axes, la contribution de chacune devrait être de 100/24 = 4,16 % pour la
détermination de chaque axe.
La matrice donnant les coordonnées des
variables sur les axes factoriels (en annexe2) laisse entrevoir que la
quasi-totalité des variables sont corrélées positivement
au premier facteur. Ce qui signifie que pour toutes les banques bien
représentées sur cet axe avec une coordonnée positive, les
scores mensuels ont été supérieurs aux moyennes mensuelles
pratiquement sur toute la période de l'étude. De même, pour
toutes les banques bien représentées sur cet axe, mais
plutôt avec une coordonnée négative, les scores mensuels
ont été inférieurs à la moyenne presque sur toute
la période de l'étude. L'examen du nuage des banques ci-dessous
permet de constater que le premier axe factoriel oppose deux groupes de banques
à gauche et à droite de l'origine. Le premier groupe situé
à droite de l'origine est constitué essentiellement de banques
camerounaises et gabonaises dont la plupart ont eu des scores mensuels
supérieurs aux moyennes mensuelles des scores sur toute la
période.
Graphique 3.5 : Projection des individus sur les
deux premiers facteurs

Source : COBAC, nos calculs
Le deuxième groupe situé à gauche
de l'origine est constitué essentiellement des banques des autres Etats
de la CEMAC. Les banques de ce groupe qui sont bien représentées
sur le premier facteur, ont eu des scores mensuels inférieurs aux
moyennes mensuelles des scores sur toute la période.
Le deuxième axe factoriel quant à lui
oppose également deux groupes de banques au dessus et en dessous de
l'origine. La matrice des coordonnées des variables sur les axes
factoriels montre que toutes les variables correspondants à
l'année 2001 sont négativement corrélées au
deuxième facteur. Ce qui signifie que pour les banques bien
représentées sur cet axe avec une coordonnée
négative, les scores mensuels ont été supérieurs
aux moyennes mensuelles durant toute l'année 2001. Il s'agit notamment
des banques gabonaises situées en dessous de l'origine dont les
contributions sur le deuxième facteur sont supérieures à
la contribution moyenne de ce facteur. De manière analogue, les banques
bien représentées sur cet axe plutôt avec une
coordonnée positive, ont eu des scores mensuels inférieurs aux
moyennes mensuelles durant toute l'année 2001. L'on constate que la
quasi-totalité des autres variables sont faiblement et positivement
corrélées au deuxième facteur.
L'ACP permet donc de distinguer dans l'ensemble deux
grands groupes :
v' Les banques gabonaises et camerounaises (et certaines
banques Tchadiennes), dont la plupart ont eu des scores élevés
pratiquement sur toute la période de l'étude ;
v' Les banques des autres Etats de la CEMAC dont
certaines ont eu des scores tantôt élevés, tantôt
faibles, et d'autres des scores faibles sur toute la période de
l'étude.
La figure ci-dessous représente l'arbre
hiérarchique obtenu en appliquant l'algorithme de Ward à notre
tableau rectangulaire constitué des banques en ligne et des scores
mensuels en colonne.
Figure 3.2 : Arbre hiérarchique issu de
l'algorithme de Ward
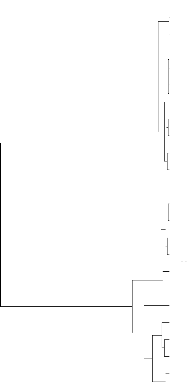
Gab4
Gab1
Gab3
Gab2
Cam3
Cam1
Cam5
Cam7
Cam4
Tcd3
Tcd2
Tcd4
Gab5
Cam2
Cam8
Tcd1
Cog8
Gnq2
Gnq1
Cam6
Tcd5
Caf2
Caf3
Caf1
Source : COBAC, nos calculs
Cet arbre met effectivement en évidence une
similarité entre la plupart des banques gabonaises et camerounaises
ainsi que certaines banques tchadiennes. En effet, en adoptant un regroupement
en trois classes, on constate que la première classe est essentiellement
constituée
de banques gabonaises et camerounaises ainsi que de
deux banques tchadiennes. La deuxième classe quant à elle, est
constituée essentiellement de banques camerounaises et tchadiennes, et
d'une banque gabonaise (la moins performante au Gabon). Enfin la
dernière, comporte toutes les banques centrafricaines et
équato-guinéennes, ainsi que l'unique banque congolaise de notre
échantillon. On retrouve également dans cette classe, une banque
camerounaise (la moins performante au Cameroun), et une banque tchadienne (la
moins performante au Tchad).
En définitive, il ressort de ce chapitre que
les banques commerciales de la CEMAC ne gèrent pas optimalement les
ressources mises à leur disposition. Elles produisent des
quantités de crédits inférieures à ce qui est
techniquement possible à partir des ressources dont elles disposent. Ce
qui justifie le fait que la production des crédits bancaires semble ne
pas couvrir entièrement les besoins d'investissements dans la
sous-région. Ce chapitre révèle également que les
banques gabonaises et camerounaises semblent avoir été dans
l'ensemble les plus efficaces dans la transformation de leurs ressources en
crédits entre 2001 et 2004.
L'investissement productif étant le moteur de
la croissance économique, il convient donc afin d'assurer son
financement, de rechercher les facteurs sur lesquels on pourrait agir pour
améliorer l'efficacité technique des banques de la CEMAC. Ce qui
nous amène à estimer le modèle économétrique
présenté au chapitre suivant.
|
|



