3.7. Détection CA-CFAR-BI-2D: (a deux
dimensions)
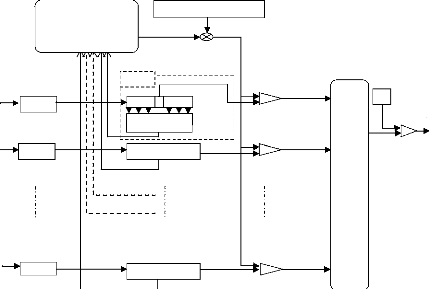
Le schéma du CA-CFAR-BI-2D s'apparente
étroitement au schéma du CA-CFAR-BI, la seule différence
est que l'estimation du signal parasite est faite à partir des cellules
de références de toutes les récurrences (L).
????
~ ????????
???? =1
Facteur d'échelle=fct
CA-CFAR 1
Ø1 =1 ???????? 0
1 ????????
SLD 1
????1 = ????????????????????(????????)
( ????)
Ø2 = 1 ???????? 0
SLD 2
CA-CFAR 2
????2
Ø???? = 1 ???????? 0
SLD L
CA-CFAR L
0
M
????
~Ø????
????=1
????????
3.7.1. Probabilité de détection du CA-CFAR-BI-2D
La formule de la probabilité de détection du
CA-CFAR-BI-2D est identique à la formule du CA-CFAR-BI, sauf que le
terme N est remplacé par le terme « NL » ; avec :
NL=N×L.
1
(1 - ????0) ~(1 - ????0) 1 + ????0
1 + ????2???? 1 + (1 + ????)????2????
1 + ????
1 1
+????0 ~(1 - ????0) + ????0
1 + ????2???? 1 + 1 + ????
1 + ???? + ???? 1 + ???? + ???? ????2????
???????? ~?
?
?
???????? ?
?
~
?
????
????
????????2???? = ~ ???????????? ×
????=????
|
????????
1 1
1 - (1 - ????0)~(1 - ????0) + ????0 ~ ?
1 + ????2????
? 1 + (1 + ????)????2???? ?
×
1 + ????
? ?
????????
? ?
? 1 1 ?
-????0 ~(1 - ????0) + ????0 ~
1 + ????2???? 1 + 1 + ????
1 + ???? + ???? ????2????
? 1 + ???? + ???? ?
|
????-????
... (3.19)
|
3.7.2. Probabilité de fausse alarme du CA-CFAR-BI-2D
La ???????????? peut être déduite en mettant «
s=0 » dans l'expression
(1 - ????0) ~(1 - ????0) 1
+????0 ~(1 - ????0) 1 + ????0
1+????2???? + ????0 1+(1+????)????2????~
1+????2???? 1+ ????2????~
1+???? ?
1
1 ???????? ?
???????? ?
????=????
× ?1 - (1 - ????0) ~(1 - ????0) 1
? 1+???? ?
-????0 ~(1 - ????0) 1 + ????0
1+????2???? 1+ ????2????~
1+????2???? + ????0 1+(1+????)????2????~ ? ???? ????
1 1 ???????? ?
???????? ???? ×
????
... (3.20)
????????????2???? = ?
????
????-????
(3.19) :
3.7.3. Performance du CA-CFAR-BI-2D
Nous procédons toujours par les trois étapes :
a) On fixe Pfa2D =10-6.
b) Le facteur d'échelle « T2D» sera
calculé après résolution de l'équation (3.20). par
la méthode de dichotomie.
c) On remplace T2D dans l'expression (3.19) et on
calcule la probabilité de détection PdR2D pour
différentes valeurs de s.
Pd en fonction du rapport SNR avec une Pfa=1e-6
Pd
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
CACFAR-BI-2D-F1F2 / e0=.05
FNR=50(dB)
0 10 20 30 40 50 60 70
SNR (dB)
Figure 3.23 : la probabilité de détection du
CA-CFAR-BI-2D en
fonction du SNR pour r=50dB, e0 = 0,05, M=4 et
L=6 et N=16.
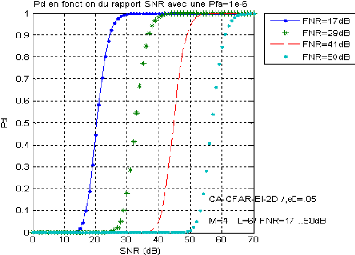
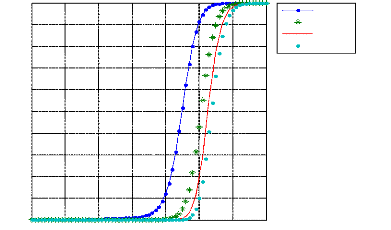
Figure 3.24 : la probabilité de détection du
CA-CFAR-BI-2D en
fonction du SNR pour ????0 = 0,05, r=17..50dB, M=4, L=6
et N=16.
Pd en fonction du rapport SNR avec une Pfa=1e-6
0.4
CACFAR-BI-2D-F1F2 / e0=0,02...0,05
0.3
FNR=50(dB)
0.2
M=4 L=6 N=16
0.1
0
0 10 20 30 40 50 60 70
Pd
0.5
1
0.9
0.8
0.7
0.6
e0=0,02 e0=0,03 e0=0,04 e0=0,05
SNR (dB)
En analysant les graphes 3.23, 3.24 et 3.25 nous arrivons
à la
conclusion que le CA-CFAR-BI-2D est le schéma le plus
performent de tous les schémas CFAR précédemment
étudiés . Ainsi pour une fenêtre de référence
très large, ce détecteur se rapproche du détecteur
optimale de Neyman-Pearson (Binaire a seuil fixe).
Les particularités du signal réponse (SSR)
suivantes vont nous permettre d'améliorer considérablement les
performances de détection :
> Les réponses SSR sont caractérisées par
les impulsions d'encadrement (F1 F2), qui sont séparées par 20,3
us
> Les impulsions d'encadrement (F1 F2) ont le même
niveau de puissance, aussi, ils ont le même niveau de puissance que les
impulsions de codages << A1 A2 A4 B1 B2 B4 C1 C4 D1 D2 D4».
| 


