3.5.3. Estimation adaptative des paramètres du FRUIT
(å0, r)
Nous constatons que l'équation (3.11) prend la forme
suivante :
F (T, r,å0) =0.
Où « å0 et r » sont respectivement la
fréquence d'apparition des impulsions FRUIT et le rapport FRUIT sur
bruit (FNR), ces deux paramètres seront évalués pour
chaque cellule test à partir de la fenêtre de
référence correspondante. Cette évaluation sera faite soit
par l'algorithme de censures automatiques [9,13 et 14], ou bien par une autre
méthode plus simple et relativement rapide que nous allons proposer.
3.5.3.1. L'algorithme de censure automatique
Les echantillons de la fentitre de reference xj, (j = 1, 2,...,
N) sont d'abord classes par ordre croissant pour former la statistique d'ordre
suivante:
y1 <y2 <............<yN--1 <yN
Nous allons ensuite chercher le keme echantillon ( yk
) à partir du quel
l'algorithme de censure automatique detecte la presence d'une
impulsion FRUIT, ainsi tous les echantillons restants contiennent
indubitablement du FRUIT. Cet algorithme fonctionne de la manière
suivante :
· Chaque element de la statistique d'ordre y~' = ( y1, y2,
... , yN ) est compare
à un seuil adaptatif d'après la règle:
yi+1 Si Ti, i = 1,2, .........,N ... (3.12)
Avec :
- Si = Zip =1 yP
- Les constantes Ti sont determinees d'après [14]
à partir de la
probabilite de fausse censure ( exp : PfC =
10--4 ).
N 1
PfC = (i ) [1+Ti(N--i)]i ...
|
(3.13)
|
|
· La procedure recursive sera arrtitee au
keme echantillon, lorsque la condition (3.12) devient vraie. Les
cellules de la fentitre reference seront ainsi divisees par rapport à
l'echantillon k en deux parties: La première partie de gauche contient
du bruit seulement, alors que la deuxième partie contient le FRUIT plus
le bruit. Les paramètres de l'interference (FRUIT) seront estimes en
utilisant cette deuxième partie [9].
· En fin, l'evaluation de la puissance (Fp) et
de la probabilite d'apparence (Ff) du FRUIT peuvent titres evaluees comme suit
[9]:
Y(N+k+1)/2
1 si N -- k est impaire
> Fp = (yN+k+yN+k+2)
2 2 2 si N -- k est paire
La puissance du FRUIT etant evaluee, le rapport FRUIT sur bruit
sera
calcule par : r = FNR = Fëp
> Ff = å0 = (N -- k)/N

Cellules de
garde
Cellules de
référence
71
|
????1 ...
|
... ... ????????/2
|
|
H1
|
|
xr2+1~ ... ...
|
... ????????
|
STD

Cellules
sous test
Classement par ordre croissant :
????1 <????2 <...... ......<????????-1 <????????

Algorithme de censure automatique :
Calcule de k



Estimation de r (FNR) et de ????0
Figure 3.8 : le schéma synoptique de l'estimateur par la
censure automatique
3.5.3.2. Méthode proposé (censure
directe)
L'algorithme de censure automatique repose sur un dispositif qui
détecte
le FRUIT et évalue les deux paramètres le
caractérisant (????0 ???????? ????) par rapport à
un seuil adaptatif évalué par un CA-CFAR estimant
le bruit à partir des cellules de gauche de la statistique d'ordre.
Puisque le bruit dans le radar secondaire est essentiellement
thermique avec une fonction de distribution connue, nous pouvons fixer un seuil
de détection pour toutes les cellules de références
à fin d'y détecté l'existence d'impulsions FRUIT.
On aura donc pour chaque cellule deux hypothèses : H0
pour le cas de présence du bruit seulement et H1 pour le cas de
présence du bruit plus le FRUIT.
-????????
???????????? (????????|????0) = 1 ????
? ???? ????
?
?
?
?
-????????
????(1+????)
???????????? (????????|????1) = 1
????(1+????) ????
... (3.14)
Le seuil de détection sera choisi pour une
probabilité de fausse censure minime.
-x???? -????
8
???????????? = ? ???????????? (xx|H0)???????????? = ? 1
8???????? ???? ???????????? = ???? ????
???? ????
|
8
???????? = ? ???????????? (xx|H1)???????????? = ? 1
8
???? ????????(1+????)????
|
-x????
|
|
-????
|
|
????(1+????) ???????????? = ????
|
????(1+????)
|
Avec ???? : le seuil de détection

1
5 × 10-4
0.3
0.2
0.1
0
-100 -95 -90 -85 -80 -75 -70 -65 -60
seuil de censure directe (dBm)
Pc et pfc
0.5
0.4
0.9
0.8
0.7
0.6
pfc
pc FNR =0dB pc FNR =6dB pc FNR =9dB pc FNR =12dB pc FNR =15dB
pc FNR =18dB
Figure 3.9 : La probabilité de censure et de fausse
censure en
fonction du seuil de détection
Nous remarquons sur la Figure 3.9 que pour un seuil de
détection de -
80dBm la probabilité de fausse censure est de 5 ×
10-4, alors que la probabilité
de censure dépend du niveau de puissance du FRUIT, et elle
n'est significative que pour FNR >9dB.
Après détection ou non détection du FRUIT
dans chaque cellule de la fenêtre de référence, nous
pouvons estimer la fréquence d'apparition des impulsions FRUIT et
ensuite le rapport FRUIT sur bruit (FNR ou r), à partir du schéma
proposé dans la Figure 3.10.
3.5.3.2.1. Estimation de la probabilité d'apparition
des impulsions FRUIT
Les sorties binaire Qi (Figure 3.10) des détecteurs de
chaque cellule de la fenêtre de référence seront
sommées et divisées par le nombre de cellule de
références (N), ceci donnera une bonne estimation de la
probabilité d'apparition
du FRUIT « ????0 ».
å0 * = ? Qi
N ... (3.15)
Avec å0 * : probabilité d'apparitions du FRUIT
estimée.
Pour que le schéma synoptique de l'estimateur par la
censure directe soit plus lisible nous avons choisi le nombre de cellule de
référence N=6 à titre d'exemple:

-80dBm
Q1
0
1 0 1 0 1
Calcul de la probabilité d'apparition du
FRUIT « ????0 >> ????0 * = ?????????
????
Q2 Q3
Q4
0 1
Q5 Q6
0 1 0 1
Estimation du
rapport FRUIT
sur bruit « FNR
>>
????0 *
r* =
? xi
N ? ë
å0 * × ë
????1 ... ... ????2 ... ... ????3
|
|
|
H1
|
|
|
????4 ... ... ????5 ... ... ????6
|
3.5.3.2.2. Estimation du rapport FRUIT sur bruit (FNR)
La moyenne statistique des « N » cellules de
référence correspond à la moyenne de la variable
aléatoire définit par la fonction de distribution
« ???????? (????|????0) » de l'expression (3.1).cette
moyenne peut être évaluée par
l'estimation :
-???? -????
E [ ???????? (????|????0) ]= ????0 × E [ ????(11+????) ????
????(1+????) ] + (1 - ????0) × E [1???? ???? ???? ]
= ????0 × ???? × (1 + ????) + (1 - ????0) ×
????
On aura donc :
? ????????
???????????? = ????= ????0 × ???? × (1 + ????) + (1 -
????0) × ????
La probabilité d'apparitions du FRUIT étant
évaluée par l'expression (3.15), la valeur de « r »
(FNR) pourra ainsi être évaluée par l'expression:
|
r* =
|
?xi
-ë
N
å0*×ë
|
...
|
(3.16)
|
3.5.3.2.3. Performance de la censure directe
Pour tester la performance de l'estimateur proposé nous
avons généré un signal contenant du bruit dont la fonction
de distribution est exponentielle (en
amont du détecteur quadratique) et dont la moyenne est
???? (???? = 1.3123 ×
10 -9) , et des impulsions d'interférences
avec une probabilité d'apparition
poissonnienne « ????0 »
et une distribution en amplitude exponentielle dont la
moyenne est ???? × (1 + ????).
Pour r=50dB et ????0 = 0.05 la forme du signal simulé est
représenté sur la
Figure 3.11 :
Avant d'appliquer l'estimation par censure directe sur ce
signal, il faut mentionner que les paramètres du FRUIT qu'ont doit
estimer à partir des cellules de références, varient
lentement d'une cellule test à la cellule test adjacente, puisque pour
deux cellules tests adjacentes les fenêtres de référence
correspondantes ne diffèrent que de deux cellules (les
extrémités de la fenêtre de référence).
x 10-7 signal simulé e0=0.05 / r=50dB

amplitude
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
0 100 200 300 400 500 600
cellule de refference
Figure 3.11 : signal simulé avec ????0 = 0.05 et
r=50dB
Ainsi on a simulé pour chaque cellule test des
paramètres FRUIT différents, mais qui varient lentement d'une
cellule à l'autre (Figure 3.12).
x 105 simulation du FNR autour de chaque cellule
test

FNR
0.5
1.5
2
0
1
0 100 200 300 400 500 600 700 800 900 1000
0.1
0.05
0
probabilite d apparition du FRUIT
cellule sous test
simulation de e0 autour de chaque cellule test

0 100 200 300 400 500 600 700 800 900 1000
cellule sous test
Figure 3.12 : simulation de ????0 et du FNR pour 1000 cellules
test
x 105 estimation du FNR autour de chaque cellule
test
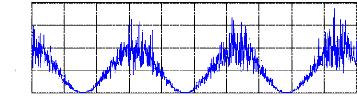
FNR
0.5
1.5
2
0
1
0 100 200 300 400 500 600 700 800 900 1000
0.1
0.05
0
probabilite d apparition du FRUIT
cellule sous test
estimation de e0 autour de chaque cellule test

0 100 200 300 400 500 600 700 800 900 1000
cellule sous test
Figure 3.13 : estimation de ????0 et du FNR pour 1000 cellules
test
adjacentes par la censure directe (N=600)
x 105 estimation du FNR autour de chaque cellule test
aprés integration

FNR
0.5
1.5
2
0
1
0 100 200 300 400 500 600 700 800 900 1000
cellule sous test
0.1
0.05
0
probabilite d apparition du FRUIT
estimation de e0 autour de chaque cellule test aprés
integration

0 100 200 300 400 500 600 700 800 900 1000
cellule sous test
Figure 3.14: estimation de ????0 et du FNR pour
1000
cellules test adjacentes (N=6000)
L'application de la censure directe nous donne une estimation
satisfaisante avec une erreur (Figure 3.13), due au fait que le nombre de
cellules de référence n'est pas assez représentatif. Nous
pouvons diminuer cette erreur par une fenêtre de référence
plus large, Nous constatons une nette amélioration de l'estimation
(Figure 3.14) qui prend des valeurs très proches des valeurs
simulées (Figure 3.12). Cependant des valeurs faibles du FNR et de e0
seront mal estimés, car dans ce cas les impulsions FRUIT seront
noyées dans le bruit.
| 


