3.5. Détection CA-CFAR: (cell averaging
CFAR)
L'objectif attendu à partir de cette partie du chapitre
consiste en l'amélioration des performances du système SSR, par
l'utilisation de la technique de détection adaptative à taux de
fausse alarme constant (CFAR).
Nous allons commencer par le détecteur CA-CFAR. Les
distributions dans la cellule sous test, pour les hypothèses H0 et H1,
sont définies par le couple suivant :
-???? -????
1
????1
????????(????|????0) = (1 - ????0) 1 ????1 ????
? ???? + ????0
avec~????1 = ????(1 + ????) ????2 = ????(1 +
????) ????3 = ????(1 + ???? + ????)
???? ????
?
?
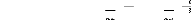
-???? -????
? 1
????????(????|????1) = (1 - ????0) 1
?????2????????2
+
????0????????3????3
3.5.1. Probabilité de détection
D'après l'expression (2.5) du chapitre 2, la
probabilité de détection s'écrit comme suit:
|
-????????
???????? = ????[?wfx(????|????1)????????] = ????[(1 -
????0)???? ????2 + ????0????
|
-????????
????3 ]
|
-???????? -????????
???????? = (1 - ????0)????[???? ????2 ] + ????0????[???? ????3 ]
... (3.6)
Nous savons aussi que la fonction génératrice des
moments MW(P)
d'une variable aléatoire W est :
MW(P) = ????[????-????????] ... (3.7)
De (3.6) et (3.7) on peut écrire :
|
???? ????
???????? = (1 -
????0)????????(????2)+????0????????(????3)
|
... (3.8)
|
Dans ce type de CFAR (CA-CFAR) le parasite est estimé par
la somme des cellules de références.
????
???? = ~ ????????
Où « N » est le nombre de cellules de
référence.
La fonction de distribution d'une somme de variables
aléatoires est définie par la convolution des fonctions de
distributions de toutes ces variables aléatoire :
????????(????) = ????????(????1|????0) *
????????(????2|????0) * ... * ????????(????????|????0)
Introduisant maintenant la transformée de Laplace de part
et d'autre :
????{ ????????(????)} = ????{????????(????1|????0) *
????????(????2|????0) * ... *
????????(????????|????0)}
? ????{ ????????(????)} = ????{????????(????1|????0)}
× ????{????????(????2|????0)} × ... ×
????{????????(????????|????0)}
????
-???? 1 -????
? ????{ ????????(????)} = ???? ~~(1 - ????0) ???? 1 ???? ???? +
????0 ????1 ???? ????1~ ~
~????
????{ ????????(????)} = ~(1 - ????0) 1 + ????????
1 1

+ ????01 + ????
Puisque la fonction de distribution ????????(????) est
définie sur [0 °°[, alors la
fonction de distribution ????????(????) est définie
aussi sur [0 co[ et la transformée de
Laplace de celle-ci est égale à sa fonction
génératrice des moments [25]:
1 ????
... (3.9)
????{ ????????(????)} = MW(P)
|
????
1
MW(P) = ~(1 - ????0) 1
1 + ???????? + ????0 1 + ????1 ????~
|
Des équations (3.8) et (3.9) on déduit que :
????
1 1
???????? = (1 - ????0) × (1 - ????0) ???? + ????0
????~
1 + ????2 1 + ????1 ????2
|
1 1
+ ????0 × (1 - ????0) ???? + ????0 ????
1 + ????3 1 + ????1 ????3
|
????
~
|
1
???????? = (1 - ????0) ~(1 - ????0) 1 ???? + ????0 1 +
(1 + ????)????
1 +
1
1
+????0 ~(1 - ????0) + ????0
1 + ???? 1 + 1 + ????
1 + ???? + ???? ????
1 + ???? + ????
????
~
1 +

????
~
... (3.10)
3.5.2. Probabilité de fausse alarme
La Probabilité de fausse alarme peut être
déduite en mettant « s=0 » dans l'expression (3.10) :
1 1 ~????
???????????? = (1 - ????0) ~(1 - ????0) 1 + ???? + ????0 1 + (1 +
????)????
????
1
+????0 ~(1 - ????0) 1 + ????0
1 + ???? 1 + ????~

... (3.11)
| 


