5.5 G'en'eration de nombre al'eatoires
Dans une simulation d'un ph'enomène stochastique, la
g'en'eration de nombres al'eatoires est primordiale, car elle sera incluse dans
le modèle et fournira, au fur et a` mesure, les 'echantillons
artificiels d'entr'ee au simulateur. Pour que ce dernier reproduise
fidèlement le ph'enomène r'eel, il est absolument n'ecessaire que
ces 'echantillons d'entr'ee suivent la même loi de probabilit'e qu'un
'echantillon construit d'observations faites sur le ph'enomène r'eel
[10].
5.5.1 G'en'eration de la demande suivant une loi de
poisson [5]
La loi de poisson mod'elise le nombre d''ev'enements
ind'ependants qui se produisent dans un intervalle de temps donn'e.
X P(ë) et on aura sa densit'e de probabilit'e :
P(X = x) = ëxe-ë
x! avec x un entier naturel et ë un r'eel positif
Sa fonction de r'epartition :
? Xx
?? ëk
e-ë k! , x = 0 ;
FX(x) = ? ?k=0
0, Sinon;
d'espérance E(X) = A et de variance V (X) = A.
Soit :
- X P(At)
- T Exp(A) o`u Exp représente la loi exponentielle On
peut montrer que :
P(X > 0) = P(T < t),
f(t) = Ae-ët T[[t>0] (T[ est le
symbole de la fonction indicatrice) F(t) = P(T < t) = 1 - e-ët
P(X > 0) = 1 - P(X = 0) = 1 - e-ët
Considérons une variable aléatoire suivant une loi
de poisson de paramètre A :
Axe-ë
P (X = x) = x! ,
- x représente le nombre d'occurrences dans [0,1]
- Les durées entre les occurrences successives suivent
une loi exponentielle de paramètre A
Si on considère (Ti)i=1 une suite de variables
aléatoires suivant une loi exponentielle Exp(A) :
x = X8
nT[[T1+T2+···+Tn=1<T1+T2+···+Tn+1].
n=1
Donc x suit une loi de poisson de paramètre A tel que
:
P(x = n) = P(T1 + T2 + ··· + Tn = 1
< T1 + T2 + ··· + Tn+1) Ane-ë
=
n!
Xn ti = 1 < Xn+ 1 ti.
i=1 i=1
'Etant donné(ui)i uniformes sur [0,1]; ti = -1
ë ln(ui).
Xn
i=1
|
-1 A ln(ui) = 1 <
|
Xn+ 1
i=1
|
-1A ln(ui)
|
|
Xn+ 1 ln(ui) < -A = Xn ln(ui)
i=1 i=1
ln n+1Y (ui) < -A = ln Yn (ui)
i=1 i=1
n+1Y (ui) < e-ë = Yn
(ui).
i=1 i=1
Donc pour générer un nombre suivant une loi de
poisson de paramètre A : - On génère des nombres
aléatoires (ui)i suivant une loi uniforme sur [0,1].
- On cherche alors le premier instant m tel que n+1Y
(ui) < e-ë.
i=1
- On pose alors x = m - 1.
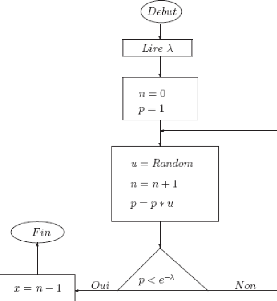
FIG. 5.3 - Organigramme pour générer un nombre
suivant une loi de poisson
Algorithme 5.1. (G'en'eration de nombre al'eatoire suivant une
loi de poisson)
D'ebut
Lire(A);
m :=0;
p :=1;
R'ep'eter
u := Random1 ;
m := m + 1;
p := p*u;
Jusqu'àp < e-ë ;
x := m - 1;
Fin
Un modèle de simulation ne peut être d'eclar'e
repr'esentatif du système r'eel sans avoir v'erifier que les
'echantillons g'en'er'es qu'il produise suivent bien les même lois de
probabilit'e que les 'echantillons tir'es a` partir des donn'ees r'ecolt'ees
sur le terrain.
On g'enère 100 nombres al'eatoire suivant la loi de
poisson de paramètre A = 48.66 repr'esent'es dans le tableau suivant
:
24
|
49
|
43
|
53
|
47
|
52
|
36
|
52
|
51
|
49
|
53
|
55
|
50
|
54
|
41
|
48
|
43
|
47
|
50
|
43
|
46
|
41
|
50
|
44
|
45
|
50
|
50
|
45
|
50
|
42
|
54
|
53
|
46
|
48
|
57
|
52
|
45
|
55
|
61
|
51
|
46
|
45
|
58
|
53
|
46
|
51
|
41
|
51
|
57
|
46
|
43
|
59
|
33
|
40
|
45
|
41
|
44
|
62
|
37
|
50
|
54
|
55
|
43
|
51
|
43
|
43
|
44
|
62
|
54
|
53
|
39
|
44
|
55
|
47
|
39
|
48
|
51
|
51
|
47
|
45
|
44
|
57
|
50
|
36
|
49
|
60
|
47
|
46
|
41
|
50
|
58
|
47
|
44
|
44
|
53
|
55
|
44
|
44
|
57
|
64
|
|
TAB. 5.1 - Nombres al'eatoires poissonniens de
paramètre A = 48.66
L'application des tests de ÷2 et de
Kolmogorov-Smirnov pour valider le g'en'erateur de nombre al'eatoires suivant
une loi de poisson de paramètre A = 48.66 donne les r'esultats suivants
:
'Random : fonction de g'en'eration d'un nombre al'eatoire
uniforme sur [0,1].
|
Test ÷2
|
Test Kolmogorov-Smirnov
|
|
Valeur
|
Valeur calculée
|
1.26 5
|
0.024
|
Valeur tabulée
|
11.07 5
|
0.13
|
|
TAB. 5.2 - Tests d'ajustement du générateur de
nombres aléatoires poissonniens
On constate que pour a = 0.05, la valeur calculée est
largement inférieure a` la valeur tabulée pour les deux tests :
l'ajustement est acceptéet donc on peut affirmer que
l'échantillon d'entrée de notre simulateur suit bien une loi de
poisson.
5.5.2 G'en'eration de la loi de service exponentielle [16]
On rencontre souvent la loi exponentielle lorsqu'il s'agit de
représenter le temps d'attente avant l'arrivée d'un
événement spécifique. Elle est souvent utilisée
lorsque le nombre de données ne permet pas de choisir efficacement entre
plusieurs distributions.
On dit qu'une variable aléatoire X suit une loi
exponentielle de paramètre u et on note X Exp(u), si sa distribution
s'écrit sous la forme :
{ ue-ux, x = 0 ; f(x) = 0, Sinon.
Sa fonction de répartition :
{ 1 -- e-ux, x = 0 ;
FX(x) = 0, Sinon ;
d'espérance E(X) = 1 u et de variance V (X) = u2 1
.
A` l'aide de la méthode de la transformation inverse, on
génère une variable aléatoire suivant une loi
exponentielle comme suit :
X = F -1(U) = -- 1 ln(1 -- U),
u
o`u U est une variable aléatoire uniforme sur [0,1].
Algorithme 5.2. (G'en'eration de nombres al'eatoires suivant
une loi exponentielle)
D'ebut
Lire(u);
u := Random;
x := -- 1 ln(1 -- u);
u
Fin
Dans le programme de simulation, on veut g'en'erer que des
dur'ees de service entières et non nulles car l'approche utilis'ee est
une approche temps. Pour ce faire, on utilise l'algorithme suivant :
Algorithme 5.3. (G'en'eration de nombres al'eatoires arrondis
suivant une loi exponentielle)
D'ebut
Lire(u);
u := Random;
k := --1ln(1 -- u);
u
x :=round2(k); Si x=0 alors x=1;
Fin
Avec cette proc'edure et en utilisant le paramètre u =
0.8111, la moyenne de l''echantillon g'en'er'e varie autour de 1.52 et ce qui
ne repr'esente pas le système r'eel (avec une dur'ee moyenne de service
'egale a` 1.23) et ne donne pas de bons r'esultats de simulation.
Pour rem'edier a` ce problème, on fait varier u
jusqu'àavoir un 'echantillon de moyenne autour de 1.23 et accepter par
les tests d'ajustement (c-à-d : qu'il est issu d'une variable al'eatoire
suivant une loi exponentielle de paramètre u = 0.8111.
Après avoir g'en'erer plusieurs 'echantillons en variant
u, on constate que la valeur qui repr'esente au mieux le système r'eel
est u = 1.21.
On g'enère 100 nombres al'eatoires en utilisant la
proc'edure de g'en'eration de nombres al'eatoires arrondis suivant la loi
exponentielle cit'ee ci-dessus avec u = 1.21. Les r'esultats obtenus sont
repr'esent'es dans le tableau suivant :
2Round : fonction qui arrondie une valeur
réelle.
1
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
1
|
3
|
1
|
2
|
1
|
1
|
2
|
2
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
1
|
1
|
3
|
1
|
2
|
5
|
1
|
3
|
2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
2
|
2
|
1
|
1
|
1
|
1
|
4
|
1
|
8
|
1
|
1
|
1
|
1
|
2
|
1
|
3
|
1
|
1
|
4
|
1
|
1
|
1
|
2
|
6
|
2
|
2
|
1
|
1
|
3
|
2
|
1
|
2
|
1
|
1
|
1
|
1
|
1
|
3
|
1
|
1
|
1
|
4
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
|
TAB. 5.3 - Nombres aléatoires de loi exponentielle de
paramètre ,t = 1.21
L'application des tests de x2 et de
Kolmogorov-Smirnov pour valider le générateur de nombres
aléatoires suivant une loi exponentielle de paramètre ,t = 0.8111
donne les résultats suivants :
|
Test x2
|
Test Kolmogorov-Smirnov
|
|
Valeur
|
Valeur calculée
|
2.52 5
|
0.055
|
Valeur tabulée
|
11.07 5
|
0.13
|
|
TAB. 5.4 - Tests d'ajustement du générateur de
nombres aléatoires de loi exponentielle
On constate que pour a = 0.05, la valeur calculée est
largement inférieure a` la valeur tabulée pour les deux tests :
l'ajustement est acceptéet donc on peut affirmer que
l'échantillon d'entrée de notre simulateur suit bien une loi
exponentielle de paramètre ,t = 0.8111.
| 


