Planification et gestion du parc de transport au niveau de la SARL Ibrahim et fils

4.3.2 Modèle sans file (avec découragement)

On considère a` nouveau le modèle pr'ec'edent avec les mêmes paramètres, mais cette fois ci sans file. Chaque camion joue le ràole d'un serveur et le modèle 'etudi'e est M/M/m( ,m) (il est a` noter que la discipline de service n'a pas de sens car il n'y a pas d'attente dans la file). Comme repr'esent'e dans le sch'ema suivant :

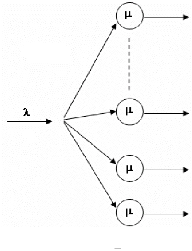
FIG. 4.4

On a

Q = 0 et W = 0 (pas de file).

T = W + 1 = 1 et N = ë(1 - ð_m)T = ñ(1 - ð_m) o`u ñ = ë/u,

u u

ð_m = ñm m! ð0 avec ð0 = 1 m _X

k=0

_ñk , k!

de plus, le nombre moyen de places occupées, par unitéde temps, est N.
Ce qui donne le nombre de places inoccupées par unitéde temps m - N.

Le bénéfice moyen journalier est donnépar:

G(m) = gN - mCf = gñ(1 - ð_m) - mCf, et ð_m est obtenu comme suit :

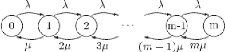
FIG. 4.5

ou encore	ðm =	1
		, ñm + m! m! ñm-1 + · · · +m(mñ2 ^-1) +^mñ + 1
ceci pour tout ñ.

Dans le modèle M/M/m+1 ( ,m+1)

1

,

(m+1)! _ñm+1 + (m+1)!

_ñm + · · · + (m+1)m

_ñ2 + m+1

ñ + 1

_ñm+1

=

(m+1)!

_ñk

ðm+1 =

k!

m+1
k=0

ce dernier dénominateur étant supérieur a` celui de ð_m, et pour tout ñ on a :

ðm+1 < ð_m.

Pour calculer _ðm+1 (probabilitéd'avoir m+1 serveurs occupés dans un système M/M/m+1 ( ,m+1)) en fonction de ð_m (probabilitéd'avoir m serveurs occupés dans un système M/M/m ( ,m)), on cherche une forme récurrente :

ðm+1 =	ñm+1 (m + 1)!^ð0						ñk ñ LJm k=0 k!
	ñm										1
=
	ñk m! Pm k=0 k!						(m + 1)				v.m+1 ñk k=0 k!
= ðm		ñ			Pm ñk k=0 k!
		m + 1			Pm+1 ñk k=0 k!
= ðm		~ Pm ~ ñk ñ k=0 k! m + 1(1 - ðm+1) car Pm+1 = 1 - ðm+1 ñk k=0 k!
d'o`u ðm+1 =			ñ m+1						et pour m = 0, on a évidement ð0 = 1.
			1 + ñm+1ðm

On calcule la variation Ä(m) = G(m) - G(m - 1) (m = 1).

Ä(m) = G(m) - G(m - 1)

= gñ(1 - ð_m) - mCf - gñ(1 - ðm-1) + (m - 1)Cf Ä(m) = gñ(ðm-1 - ð_m) - Cf

On calcule Ä(m + 1) - Ä(m) :

Ä(m + 1) - Ä(m) = gñ(ð_m - ðm+1 - ðm-1 + ð_m) = gñ(2ð_m - ðm+1 - ðm-1)

Le signe de Ä(m + 1) - Ä(m) est de même signe que (2ð_m - ðm+1 - ðm-1) car gñ est toujours positif.

On accepte sans démontrer que Ä(m + 1) - Ä(m) = 0 car les calculs s'avèrent très longs. Pour des différentes valeurs de m on calcule (2ð_m - ðm+1 - ðm-1), comme le montre le tableau suivant :

m	1	2	...	81	82	...	139	140
(2ðm - ðm+1 - ðm-1)	-8.81	-9.23	...	-0.00013	-0.00010	...	-9.785	-4.269

TAB. 4.1 - Variation de la fonction (2ð_m - ðm+1 - ðm-1).

On a Ä(m + 1) - Ä(m) = 0 donc Ä(m) est décroissante pour tout m, ce qui entraàýne la concavitéde G. Et Ä(m + 1) - Ä(m) = 0 s'écrit sous la forme :

G(m + 1) - G(m) - G(m) + G(m - 1) = 0 soit : G(m) = G(m+1)+G(m-1) .

2

Et on peut l'expliquer par le schéma classique d'une fonction concave. l'axe d'abscisses correspond au nombre de camions et les ordonnées au gain moyen journalier.

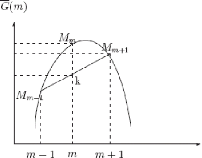
FIG. 4.6 - Schéma classique d'une fonction concave

Sur le schéma ci-dessus, on constate que l'ordonnée du milieu k de la corde Mm-1Mm+1 est au dessous du point M_m d'abscisse m et d'ordonnée G(m). Tel que :

- k correspond au point de coordonnées (m,G(m+1)+G(m-1)

₂ ).

- Les ordonnées des points respectivement _Mm-1, M_m et _Mm+1 correspondent aux
gains moyens journaliers pour respectivement un parc de m-1, m, et m+1 camions.
La valeur de m^* qui maximise la fonction gain G et celle qui satisfasse Ä(m^*) = 0
et Ä(m^* + 1) = 0. C'est a` dire que pour trouver m^*, il suffit de calculer les Ä(m) et
dès qu'on ait une valeur négative, le m correspondant n'est autre que la valeur optimale m^*.

Pour différentes valeurs du gain moyen journalier, on aura le tableau suivant :

g = 40000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	1436,18	435,55	-459,19	-	-	-	-	-	-
g = 50000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	2985,86	1735,06	616,63	-367,21	-	-	-	-	-
g = 60000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	4535,54	3034,58	1692,46	511,84	-509,67	-	-	-	-
g = 70000DA
m	...	74	75	76	77	78	79	80	81	. . .
Ä(m)	+	6085,22	4334,10	2768,29	1390,90	199,13	-815,05	-	-	-

TAB. 4.2 - Variation de la fonction Ä(m).

4.3.2.1 Interprétation des résultats

Avec les conditions normales de rentabilité(c-à-d le gain moyen journalier dépasse les coàuts fixes) et la demande considérée, on remarque qu'en partant d'une flotte de taille 0 et en augmentant a` chaque fois cette dernière d'un camion, le gain augmente car il n y aura pas de coàuts engendrés par des camions inutilisés. Mais dès que le nombre de camions dépasse une certaine limite, le surplus de camions inutilisés qui dépasse le besoins considéré, induit la décroissance de la fonction gain.

Pour les différentes valeurs du gain considérées, on obtient les dimensions de la flotte suivantes :

Valeur du gain	40000	50000	60000	70000
Dimension de la flotte	75	76	77	78