4
D'etermination du nombre de camions
4.1 Introduction
La mod'elisation est sans doute l''etape la plus importante
dans une 'etude quelle qu'elle soit. Avant de d'eterminer un modèle
math'ematique utilis'e en recherche op'erationnelle et d'expliquer les
m'ethodes qui sont g'en'eralement mises en oeuvre a` partir de ces
modèles pour obtenir des conclusions int'eressantes, nous nous
efforcons de faire apparaàýtre la nature propre du
sujet et le domaine a` l'int'erieur duquel vont se placer nos
pr'eoccupations.
Dans ce chapitre, nous allons nous efforcer de se rapprocher
le plus possible de la r'ealit'e, en pr'esentant pour chaque problème
son modèle math'ematique correspondant, et avec plusieurs approches si
c'est possible.
4.2 Problématique
On veut d'eterminer le nombre de v'ehicules qui r'epond le
mieux aux exigences de l'entreprise compte tenu de la demande
journalière, des diff'erentes destinations et leurs distance (dur'ee de
services) respectives, la capacit'e de production et le profit r'ealis'e ou
coàut engendr'e par v'ehicule.
4.3 Approche par files d'attente
4.3.1 Modèle avec file
On considère un parking de camions o`u les clients
arrivent selon un processus de poisson de taux ë, le service correspondant
a` une livraison par un camion, et les dur'ees de
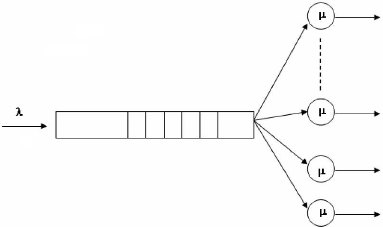
service sont indépendantes et suivent toutes une loi
exponentielle de moyenne 1/u. Dans cette approche, nous allons
représenter chaque véhicule par un serveur et les demandes
journalières par des clients. Dans le chapitre trois (tests et
ajustements), nous avons pu ajuster la loi qui régisse la demande
journalière et cela pour déterminer le processus d'arrivée
des clients qui est un processus poissonnien de taux A = 48.66 camions/jour.
Quand a` la loi de service, pour chaque camion, elle est exponentielle de taux
u = 0.8111.
En résumé:
- Le nombre de serveurs est m, a` déterminer, et sont
tous identiques avec la même loi de service qui est exponentielle de
moyenne1 u (le temps nécessaire pour livrer et revenir a` l'usine).
- Les clients arrivent selon un processus de Poisson de taux A et
sont servis selon leur ordre d'arrivée suivant la discipline (FIFO).
- La capacitéde la file est infinie.
Donc le modèle a` étudier est un modèle
M/M/m (FIFO,8) comme représentédans le schéma suivant :
FIG. 4.1 -
Avec cette approche, pour déterminer le nombre de
serveurs, on va utiliser les caractéristiques du système et
ensuite faire le chemin inverse. Le but de l'entreprise est de satisfaire la
demande de sa clientèle et de réaliser le maximum de profit
possible, et pour cela, soit on fixe le nombre de clients, soit le temps
d'attente dans la file puis déterminer le nombre de serveurs
correspondant.
Comme mentionnedans le chapitre deux (Rappels theoriques), le
temps d'attente W et le nombre de clients dans la file Q se calculent comme
suit :
La longueur moyenne de la file Q est :
|
Q =
|
8
E
k=m+1
|
mm
(k - m)ðk = ð0
m!
|
8
E
k=m+1
|
(k - m)( r n
ñn)k = 7ro
ñrm!
cE°
k=1
|
k( ñ )k,
m
|
ñ
ñm+1
soit ñm 1 m \
Q = 7ro m! (1-- m)2 ) = 70
(m--1)!(m--ñ)2 .
|
On a aussi Q =
|
8
E
k=m+1
|
8
kðk - m V
z_.,
k=m+1
|
ðk = N - (
|
m
E
k=1
|
kðk +
|
8
E
k=m+1
|
mðk) = N - ñ.
|
|
ñ =
|
m-1E
k=1
|
kðk -
|
m-1
E
k=0
|
mðk + m (car
|
8
E
k=0
|
ðk = 1),
|
Avec

k=0
1-1
.
Fm-1 ñk ñm
ð0 = [E+
k! m!(1 - mñ )
Pour eviter l'engorgement, il faut que la condition
d'ergodicitesoit verifiee : mñ < 1 soit ë < mu.
Avec les param`etre du syst`eme ë = 48.66 et u = 0.8111, on
aura : m > ë/u = 59.99 donc il faut avoir au moins 60 camions.

Le nombre moyen de clients dans le syst`eme N est : N = Q +
ñ .
Le temps moyen d'attente dans la file est : W = Që .
Le temps moyen d'attente dans le syst`eme est : T = Në = W
+ 1u .
Le nombre moyen de camions inoccupes, d'apr`es l'equation des
debits on a :
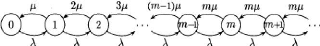
FIG. 4.2 -
8 m-1 8
E ëðk = E kuðk +
E muðk,
k=0 k=1 k=m
8 m-1 8
ë E ðk = u( E kðk +
E mðk),
k=0 k=1 k=m
d'o`u m-1X (m - k)ðk = m - p.
k=0
Si on note par g le gain moyen d'un camion et par Cf le
coàut fixe engendrépar un camion par unitéde temps (jour),
alors le gain moyen journalier G pour un parc de m camions est :
D'apres le théoreme de Burke, le nombre moyen de clients
servis par unitéde temps est A. Ce qui donne
G(m) = gA - mCf.
Donc pour différentes valeurs de m, on obtient le tableau
suivant :
|
Nbr de serveurs
|
60
|
61
|
62
|
63
|
64
|
65
|
66
|
67
|
68
|
69
|
|
Q/(jours)
|
8100,61
|
50,70
|
21,54
|
12,09
|
7,57
|
5,02
|
3,44
|
2,40
|
1,70
|
1,21
|
|
N/(jours)
|
8160,60
|
110,69
|
81,53
|
72,08
|
67,56
|
65,01
|
63,43
|
62,40
|
61,69
|
61,20
|
|
W(jours)
|
166,47
|
1,04
|
0,44
|
0,24
|
0,15
|
0,10
|
0,07
|
0,04
|
0,03
|
0,02
|
|
T(jours)
|
167,70
|
2,27
|
1,67
|
1,48
|
1,38
|
1,33
|
1,30
|
1,28
|
1,26
|
1,25
|
|
Nbr de serveurs
|
70
|
71
|
72
|
73
|
74
|
75
|
76
|
77
|
78
|
79
|
|
Q/(jours)
|
0,87
|
0,62
|
0,44
|
0,31
|
0,22
|
0,16
|
0,11
|
0,07
|
0,05
|
0,03
|
|
N/(jours)
|
60,86
|
60,61
|
60,43
|
60,31
|
60,21
|
60,15
|
60,10
|
60,07
|
60,04
|
60,03
|
|
W(jours)
|
0,01
|
0,01
|
0,009
|
0,006
|
0,004
|
0,003
|
0,002
|
0,001
|
0,001
|
7,83E-04
|
|
T(jours)
|
1,25
|
1,24
|
1,24
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
|
Nbr de
serveurs
|
80
|
81
|
82
|
83
|
84
|
85
|
86
|
87
|
88
|
. . .
|
|
Q/(jours)
|
0,02
|
0,01
|
0,01
|
0,008
|
0,005
|
0,003
|
0,002
|
0,001
|
E-04
|
~
|
|
N/(jours)
|
60,01
|
60,01
|
60,00
|
60,00
|
59,99
|
59,99
|
59,99
|
59,99
|
59,99
|
~
|
|
W(jours)
|
E-04
|
E-04
|
E-04
|
E-04
|
E-04
|
E-05
|
E-05
|
E-05
|
E-05
|
~
|
|
T(jours)
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
1,23
|
~
|
4.3.1.1 Interprétation des résultats
Pour minimiser le nombre de clients ou le temps d'attente dans
la file et par conséquent répondre au mieux aux exigences de la
clientele, on doit disposer du maximum de camions possible a` la limite de la
capacitéde production, c'est un objectif qui est directement
proportionnel a` la taille de la flotte. Par contre, réaliser le plus
grand profit tout en évitant l'engorgement impose de limiter la taille
de la flotte a` 60 véhicules. Des que le nombre de camions
dépasse les 60, le gain moyen journalier G décroàýt
et cela est dàu aux coàuts fixes engendrés par
l'inactivitédes camions par unitéde temps, donc c'est un objectif
qui est inversement proportionnel a` la taille de la flotte.
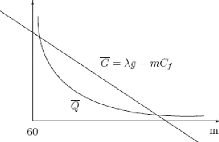
FIG. 4.3 -
|
|



