Analyse et modélisation d'un glissement de terrain. Cas de Sidi Youcef (Béni Messous, Alger )

II-4-1-5- Méthode de l'équilibre des moments [11]:

. Méthodes faisant appel à des hypothèses sur la valeur des efforts inter tranches :

Le principe de base de toutes ces méthodes est de découper le volume de sol étudié en un certain nombre de tranches et d'appliquer les différentes forces comme le montre à titre indicatif la figure. Toutes ces méthodes ont en commun la même difficulté qui est de trouver à la fois:

· la surface critique;

· les contraintes normales et tangentielles le long de cette surface;

· le facteur de sécurité (sur le critère de rupture) en partant des équations d'équilibre.

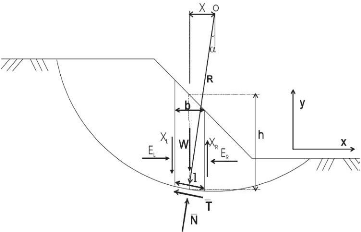
Figure II-5: Exemple d'une rupture circulaire.

Comme on peut le voir sur la figure, les forces agissant sur la tranche peuvent être définies comme suit :

W = poids total de la tranche de largeur b et de hauteur h

N, T = composantes normale et tangentielle de la force agissant à la base de la tranche

X, E = composantes verticale et horizontale des forces inter tranches.

b = épaisseur de la tranche (b=l.cosá)

á = angle que fait la base de la tranche avec l'horizontale R = rayon du cercle de rupture de centre o

l = longueur du plan de glissement de la tranche

x = bras de levier du poids des terres Définissons les efforts comme suit:

N=ól et m T=ô l

Où ô _m est la contrainte de cisaillement mobilisée à la base de la tranche qui peut être exprimée par:

T

T_m = FS

Où ô est donnee par l'equation de Mohr- Coulomb: ô =c'+ (ó?u) tanö'

Fs est le facteur de securite par lequel la resistance au cisaillement du sol doit être reduite pour amener la masse de sol dans un etat d'equilibre limite.

Il vient alors:

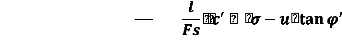
T

T = l

Fs

=

Ou :

1

T=Fs 1'l+ (N

- uI) tan q

~

Pour une tranche:

· En projetant verticalement toutes les forces:

N cos a + T sin a = W - (XR - XL)

Si on remplace T par sa valeur on obtient:

ER - EL = Nin a -

1 [~~~ + (~~ - ~~) ~~~ ~'] ~~~ ~ ~~

On peut definir le coefficient de securite comme suit:

1. soit on le definit à partir de l'equilibre moment de toutes les forces et on va le designer par Fm;

2. soit on le definit à partir de l'equilibre global des forces horizontales, les unes tendant à bouger la masse de sol, les autres tendant à la stabiliser, et on va le designer par Ff. Equilibre global des moments:

ÓW.x = ÓT.R et si on remplace T par sa valeur et x par R siná :

Fes` =

?W sina

?[E'l + (W - ul)tan to

'

Equilibre global des forces:

En absence de tout chargement de la masse de sol etudiee:

~ ER - EL = 0

~XR - XL = 0

D'où, l'equation donne:

~ ?N

hin a

~

?[~~~ + (~

~~ =

- ut) tan q^']cos a

1- Bishop:

I [~~ +

Fs & - u)tan to'

Au contraire de la methode de Fellenius, Bishop prend en consideration les forces entre

tranches ; et de même façon que la première methode :

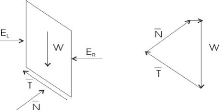
Figure II-6: Forces appliquées sur une tranche dans la méthode de Bishop. La force verticale totale W_n + ?T

~?~~

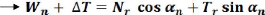
~~ + ?~ - sin a_n

Fs

tan (I) sin a_n

N, =

cos ~~ + Fs

La somme des moments :

n=p n=p

n=1 n=1

~ ~~ ~ ~~~ ~~ = ~ ~~ ~ (~ + ~~ ~~~ ~) (? ~~)(~) ? i_n

? (~?~~ + (~ ~~~ ~~ - ~ ? ~~)) ~~~ ~

~~~

~~~

~~ = --

? ~~ ~~~ ~~

~~~
~~~

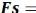
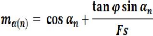
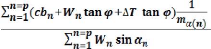
2- Fellenius :

Fellenius suppose en général, que les forces entre tranches peuvent être négligées, parce qu'elles sont parallèles aux bases des tranches. Ce faisant, on ne respecte cependant pas le principe de Newton d'égalité de l'action et de la réaction, et suggère que la résultante des forces qui agissent sur chaque tranche est nulle dans la direction normale.

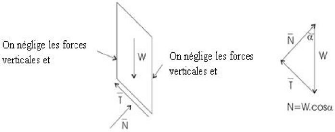
Forces sur une tranche :

Figure II-

7: Forces

appliquées

sur une

tranche dans la méthode de Fellenius

Si la tranche est en équilibre, ces forces doivent satisfaire les 3 conditions d'équilibre. Les inconnus et équations pour un système de n tranches est :

· n équations des moments pour chaque tranche; ÓM = 0.

· n équations des forces verticales pour chaque tranche; ÓFy = 0 3n.

· n équations des forces horizontales pour chaque tranche; Ó Fx = 0.

Les équations de translations ou d'équilibre donnent respectivement :

>

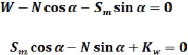
Verticalement :

> Horizontalement : Expression oil les termes ( S_m sin a, S_m cosa) présente l'effet de l'eau a l'amont et a l'aval et K_w l'effet des séismes, ces termes seront négligés par la suite pour des raisons de

simplifications des calculs, ce qui donne l'expression « La méthode de Fellenius simplifiée ». Avec les suggestions de « Fellenius », l'évaluation de la contrainte normal pour tous les points le long de la ligne de glissement, sont devenues possibles et on a :

Ni = Wi cos ai - Ui?Li

Connaissant la valeur de N_i et les paramètres C,cp du sol, devraient possible d'évaluer la force en chaque point d'élément du massif :

Si = Ni tan (I) + C?LT = (Ni cos ai - Ui?Li) +

Cb

cos ai

Par conséquent le moment autour du centre du cercle des forces résistantes à :

n n

~ Cb

SiR = l R (Ni cos ai - Ui?Li ) +

cos ai

i=1 i=1

De même le moment autour du centre du cercle des forces motrices à :

n

n

n

~ Wixi = Wi sin aiR = R1W sin ai

i=1

i=1

i=1

Comme on à mentionner auparavant, le coefficient de sécurité relatif au cercle de rupture choisit est défini comme le rapport entre les moments résistants et les moments moteurs par rapport a " O ", il vaut donc

F_s = ? ~~~ + (~~ ~~~ ~~ - ~~~~) ~~~ ~

~

~~~

? Wi sin ai

~

~~~

Autre simplification :

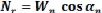
Equilibre des forces :

La force de cisaillement résistant :

~f?L7 Tr = rd?Ln = Fs La contrainte effective normale, ó'		1 =lFs + a^' tan (p)?Ln
Nr = ?Ln	Wn cos an
	?Ln

La somme des moments autour de O

n=p n=p

n=1 n=1

~~~ ~ ~~~ ~~ = ~ ~~ ~ ( ~ + ~~ ~~~ ~~ ~~~ ~)?~~ ~ ?L_n

? (~?~~ + ~~ ~~~ ~~ ~~~ ~)

~~~

~~~

~~ =? En=1 ^n=P W_n sin ^an