II-4-1-3- Méthode d'analyse globale :
. Méthode de TAYLOR (1948) ou
méthode du cercle de frottement [14]:
Lors d'une étude d'équilibre d'une pente infinie,
le poids du sol contribue aux forces déstabilisatrices alors que la
cohésion cu contribue aux forces d'équilibre. Ainsi,
la cohésion Cu et inversement proportionnelle au poids
volumique du sol ã. Elle est donnée par la formule suivante :
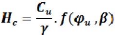
Pour que cette expression soit correcte de point de vue
dimension, la fonction f (öu ,â) doit
être une fonction sans dimensions.
|
=l Cu ~
|
km/m2 Firm.
km/m2 1-Wu ,~)sans ~imension
|
TAYLOR (1948) exprima cette fonction f(öu
,â) par un nombre appelé nombre de stabilité
Sn ou Ns

En s'appuyant sur le principe de la méthode de cercle de
frottement, TAYLOR publia le coefficient de stabilité d'un talus
homogènes en fonction de öu et
â sous forme de tableaux et d'abaques ABQ 2.1. Pour
öu =0 et â< 53°
la valeur de Sn dépends aussi du coefficient de
profondeur Df ou (Df .H)
est la profondeur de la couche de sol ferme.
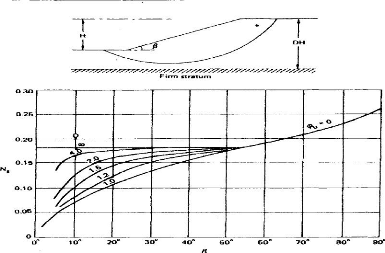
Abaque 1 : Coefficient de stabilité de
TAYLOR
|
Â
|
Ö
|
|
0°
|
5°
|
10°
|
15°
|
20°
|
25°
|
|
90°
|
0.261
|
0.239
|
0.218
|
0.199
|
0.182
|
0.166
|
|
75°
|
0.219
|
0.195
|
0.173
|
0.152
|
0.13
|
0.117
|
|
60°
|
0.191
|
0.162
|
0.138
|
0.116
|
0.097
|
0.079
|
|
45°
|
0.170
|
0.136
|
0.108
|
0.083
|
0.062
|
0.044
|
|
30°
|
0.156
|
0.110
|
0.075
|
0.046
|
0.025
|
0.009
|

15°
0.145
0.068
0.023
-
-
-
Tableau II-3 : Nombre de stabilité de
TAYLOR.
II-4-1-4- Méthode de l'équilibre des
forces [15] :
. La méthode de Coin :
Il s'agit d'une méthode approximative. La masse sur le
plan de rupture potentiel est séparée en une série de
coins et l'équilibre de chaque coin est considéré.
> Équilibre des forces horizontales et verticales.
> On doit cependant faire une hypothèse sur
l'inclinaison de la force entre les coins : 10o < d <
15o - d = 0o conservateur.
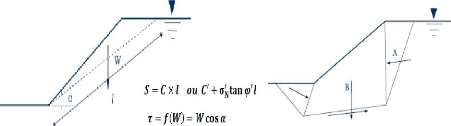
ces appliquée dans la méthode des coins.
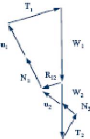
- En A et B, on voit que en plus de la translation du bloc sous
son propre poids, il y'aurai des efforts à chacune des
extrémités.
- En A semblable à pousser sur un mur
- En B semblable à buté sur un mur
- On retrouve donc deux façons de traiter ce
problème.
- D'abord on fait l'équilibre des forces sur les blocs
où on
considère toutes les masses, incluant celles à
l'extérieur.
- Problème : il faut maintenant considérer
l'interaction des coins. - On assume un facteur de sécurité de
départ. Résolution par
polygone des forces du coin 1 (on obtient R12). R21 étant
égal à
R12, le polygone des forces du coin2 doit fermer si
équilibre.
- Si le polygone ne ferme pas, il faut assumer un autre Fs.
| 


