Analyse et modélisation d'un glissement de terrain. Cas de Sidi Youcef (Béni Messous, Alger )

II-3- RUPTURE PLANE [12]:

II-3-1-Pente semi-infinie terrain sec :

Soit un élément de volume de sol ABCD de hauteur H et de largeur b qui glisse sur sa base CD.

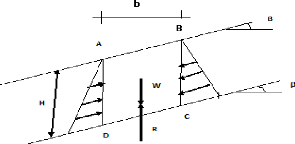
Figure II-1: Notations pour le calcul de la stabilité d'une pente.

Les diagrammes triangulaires le long d'AD et le long de BC sont égaux et opposés. On considère que la réaction R du terrain est égale au poids W de l'élément ABCD. Cette réaction se décompose en une composante normale à la face DC notée N et une composante parallèle à la face DC notée T.

N = WX cos â = ãX bX HX cos â. T = WX sin â = ãX bX HX sinâ.

On déduit les contraintes moyennes le long de CD :

ó =N / (b / cos â) = ãX HX cos² â

ô= T/(b / cos â) = ãX HX sinâX cos â.

En retenant comme critère de rupture par glissement la loi de coulomb :

ô = ó tg ö + C il vient:

ãX HX sinâX cos â= ãX HX cos² âX (tg ö + C).

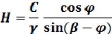
D'ou l'on tire l'expression suivante :

Si â <ö.

L'application de l'équation donne pour H <0 donc aucune

ligne de glissement ne peut se produire et la pente est stable d'où :

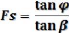
Si â = ö

L'expression donne pour H une valeur théoriquement infinie et la pente est en état d'équilibre limite donc

Fs = 1.

Si â >ö

Le talus est instable et l'équation de H permet d'apprécier la profondeur maximum prise par la ligne de glissement.

II-3-2-Pente semi-infinie avec écoulement :

Soit une pente semi-infinie qui est le lieu d'un écoulement parallèle à la pente à la profondeur z :

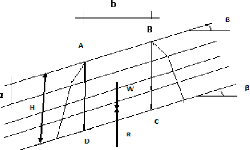
Figure II-2 : Notations pour le calcul de la stabilité d'une pente avec écoulement.

Les diagrammes de poussée des terres le long de AD et le long de BC sont considères égaux et opposés. On en contrainte moyenne le long de DC pour calculer l'équilibre. On déduit les contraintes effectives moyennes appliquées le long de CD :

Fs Tmax T =l	=	((Yh × z) + (Ysat -- Yw)(H -- z)) cos^2 # × tan p' + C^'
		((Yh × z) + Ysat × (H -- z)) sin # × cos #

ômax : résistance au cisaillement du sol ;

ô: contraintes de cisaillement s'exerçant le long de la surface. II-4- RUPTURE CIRCULAIRE :

II -4-1- METHODE D'EQUILIBRE LIMITE :

L'étude de la stabilité des pentes est d'une importance primordiale dans le dessin des excavations, des digues, des barrages, des autoroutes, etc. En général, la méthode universellement utilisée est celle de l'équilibre limite .On considère l'aptitude au glissement d'un certain volume de sol au voisinage de la pente.

II -4- 1-1- Principe :

Pour illustré le principe on va étudier l'équilibre d'un bloc sur une pente avec un angle quelconque, on considère uniquement l'action de la force dus au poids propre de la masse qui conduit le bloc a ce déplacer. On dit que le bloc est en équilibre si la somme des forces internes égale à 0.

La composante du W qui rend ou bien qui met le bloc en mouvement est : Wsin á La composante du W entre la base du bloc et la surface de glissement est : Wcosá

La contrainte appliquée normale à la surface de contact est : ó = (F)/ A. telle que F = W cos á ó = (W cos á)/ A.

A : la surface de contacte.

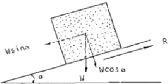
Figure II-3 : Schéma représentatif des forces appliqué sur un bloc.

La contrainte tangentielle (cisaillement) est définie par le critère de rupture de Coulomb : ô = c + ó tg ö

ô = c + ((W cos á)/ A) tg ö.

La force de cisaillement (R = ô.A) qui résiste au glissement. L'égalité avec le critère donne : R = cA+ (W cos á) tg ö.

L'équilibre de la masse est satisfait lorsque la force qui cause le mouvement est en égalité avec la force opposée qui stabilise la masse, donc :

R = W sin á => W sin á = cA+ (W cos á) tg ö

Si :

C = 0 => W sin á = (W cos á) tg ö. Et si á = ö =>W sin á = W sin á (le bloc est en équilibre)

II -4-1- 2- Hypothèses classiques de la méthode de l'équiibre limite [13] : La méthode est basée sur les hypothèses suivantes :

- Le problème est supposé bi-dimensionnel.

- Il existe une ligne de glissement.

- Le coefficient de sécurité F traduit l'écart entre l'état d'équilibre existant et l'état d'équilibre limite :

- Le sol est considère comme ayant un comportement rigide plastique avec le critère de Coulomb ô = C + ó tg ö. La rupture, si elle a lieu, se produit en tout point d'une ligne de glissement continue en même temps (pas de rupture progressive) .

- Le coefficient de sécurité F traduit l'écart entre l'état d'équilibre existant et l'état d'équilibre limite :

Fs= _ôlim /ô = (C + ó tg ö) / (C + ó tg ö_c)

A Fs peuvent être associés deux autres coefficients de sécurités :

> L'un relatif à la cohésion : F_c = C /C_c

> L'autre à l'angle de frottement : F_ö = tg ö / tg ö_c.