II-4-1-6--Méthodee del'équilibree des
forces et des moments :
·Méthodess faisant
deshypothèsess sur lalignee
depousséee[16]1 : 1-
Jambugénéralisée::
La méthode généralisée de Jambu
(Jambu 1973)considèree les deux forces inter-tranches et suppose une
ligne de pousséeafinm dedéterminerr une relation des forces
inter-tranches. Parconséquent,, le coefficient de
sécurité devient une fonction complexeàa la fois avec les
forces inter-tranches :
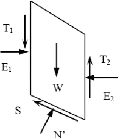
FigureII-88 : Lareprésentationn des
forces sur une tranche?(t'tt + (~ --- u/)tann v')sinn
a
FS =l?(W - {~2 - Ti}tann a +l
?(E22 --- El)1
Demême,, la force totale normaleàa la base (N)
devient une fonction de la force inter tranche de cisaillement (T) comme:
|
N =
|
~~ ~~ - (~~ - ~~) - ~
~ ~ (~~~ - ~~ ~~~ ~') ~~~ ~~
2- Jambu simplifié :
|
La méthode simplifiée de Jambu est un indice
composite basé sur des surfaces de cisaillement (c'est-à-dire non
circulaire) et le coefficient de sécurité est
déterminé par l'équilibre des forces horizontales. Comme
dans la méthode de Bishop, la méthode considère les forces
inter-tranches normales, mais néglige les forces de cisaillement (T). La
base de la force normale (N) est déterminé de la même
manière que dans la méthode de Bishop et le coefficient de
sécurité est calculé par:
|
Fs =
|
?(V/ + (N - u/) tan ~') l
cos a
? Wtan a + ? ?E
|
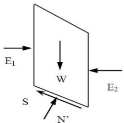
Figure II-9: Représentation des forces
sur une tranche.
? ?E = El - E2 (Zéro s'il n'y a pas de force
horizontale).
Jambu introduit un facteur de correction (
f0 ), dans le coefficient de sécurité
F0 ,
pour tenir compte des effets des forces inter-tranches de
cisaillement. Avec cette modification, la méthode de Jambu
corrigé donne un coefficient de sécurité supérieur,
comme:
Oil :
F =
Ff = foF0
?(P(t' + (P - u)tanv')
na
? pb tan a
Et :
~~ = ~~~2 ~(~ + ~~~ ~ ~~~ ~~ F
C'est un facteur de correction qui varie en fonction de la
profondeur à la longueur de la masse de la terre glissante et du type de
sol.
P=W/b=contrainte totale verticale ;
b= largeur d'une tranche.
· Méthodes faisant appel à
des hypothèses sur l'orientation des efforts inter tranches
:
1- Méthode de spencer
:
La méthode de Spencer est initialement
présentée pour les surfaces de rupture circulaire, mais la
procédure peut être facilement étendu aux surfaces de
rupture non circulaires.
Spencer (1967) a mis au point deux équations de
coefficient de sécurité, l'un à l'égard de
l'équilibre des forces horizontales et un autre à l'égard
de l'équilibre de moment. Il a adopté un rapport constant entre
les forces inter- tranches de cisaillement et normal.
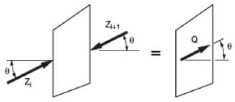
Figure II-10: Résultante des forces
parallèles L'équation de l'équilibre des forces:
1Qi = 0
Et :
Qi = Zi -- Zi-Fi
Parce que les forces inter tranche sont supposées
être parallèles, Qi , Zi ,
et Zi + 1 ont la même direction et
Qi est tout simplement est la différence scalaire
entre les forces intertranches de gauche et de droite de la tranche
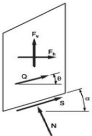
Figure II-11: Représentation de toutes
les forces inconnues sur une
tranche dans la méthode de Spencer.
L'équation d'équilibre des moments est
exprimée par la relation :
1QEirb sin 0 -- yQ cos 0) = 0
Figure II-12: Les coordonnées pour une
surface de rupture non circulaire utilisée dans la
méthode de
Spencer.
Après une série de calcul Spencer a trouvé
une expression réduite pour le coefficient de sécurité
comme suite :
( 2 = ~~~ ~~~ ~~~~ ~~~ ~~~~~?~
cos(_o)l[sin(l-O)tan epll
~ ~~(~~ ~~~ ~~~~ ~~~ ~~~?~)(~~~~~
F ~ )
Méthodes Morgenstern et Price.
La méthode de Morgenstern et Price aussi satisfaire
à la fois les forces et les moments et suppose une fonction des forces
inter-tranches. Selon Morgenstern - Price (1965), l'inclinaison des forces
inter-tranches peut varier par une fonction arbitraire (f (x)) comme:
7' = f(i)RE
Les forces considérées sont indiquées dans
la figure:
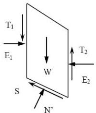
Figure II-13: Représentation graphique
des forces sur une tranche.
Oil :
f(x) : Fonction des forces
inter-tranches qui varie continuellement le long de la surface de rupture,
A : Facteur d'échelle de la
fonction supposée.
La méthode propose tout type assumant la fonction de la
force, par exemple un demisinus, trapézoïdal ou autre. Les
relations de la force normale à la base (N) et les forces intertranches
(E, T) sont les mêmes que dans la méthode générale
de Jambu. Pour une fonction de force, les forces inter-tranches sont
calculées par la procédure d'itération jusqu'à ce
que, Ff est
égal à Fm dans les
équations
?[{cf/+(1--u/)tan vr}cos cc]
F
=
l
f ? {ig-- (1'2 --Ti)}Itan a+?(IE2 --Ei
)l
Et
~~ = ?(~~~~(~~~~) ~~~ ~~
?W sin a
En générale cette méthode :
· Considère les deux forces inter tranches,
· suppose une fonction des forces inter-tranches f (x),
· Permet la sélection de la fonction des forces
inter tranches,
· Le coefficient de sécurité est
calculé à la fois par les équations d'équilibres
des forces et des moments.
| 


