3- La sensibilité :
La sensibilité peut se définir comme la
variation du cours d'une obligation, entraînée par la variation
d'un point du taux d'intérêt sur le marché obligataire. La
sensibilité est exprimée en pourcentage, et elle est en principe
négative, puisque la hausse de taux entraîne une baisse des cours
des obligations à taux fixe.
Mathématiquement, la sensibilité d'une obligation
peut s'écrire :
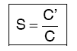
Avec :
· C : cours de l'obligation à la date
considérée,
· C' : dérivée première de la
fonction mathématique exprimant le cours (c) de l'obligation par rapport
à un taux (t).
Une autre expression de la sensibilité est mise en
évidence par le biais de la duration (D) :
S = -D/(1+t)
En résumé, la sensibilité permet de
mesurer le degré d'exposition au risque de taux d'une obligation.
Rappelons que le cours des obligations évolue en sens
inverse des taux d'intérêt sur le marché obligataire. Ce
qui explique que la sensibilité soit exprimée avec un signe
(négatif).
La sensibilité est un paramètre important dans
la gestion du risque et donc des performances d'un portefeuille d'obligations.
Un gestionnaire qui anticipe une baisse des taux d'intérêt sur le
marché (et donc une hausse des cours des obligations) devra acheter des
obligations à taux fixe, à forte sensibilité, s'il veut
accroître ses performances de son portefeuille obligataire.
3- La convexité :
La sensibilité, ou duration modifiée, donne une
bonne mesure de la variation du prix occasionnée par une très
petite variation de taux (1%). Pour des variations plus grandes, la
sensibilité fournit une estimation de la variation du prix beaucoup
moins précise. La raison de cette perte de précision est
expliquée par la forme convexe, et non linéaire, de la relation
entre le prix et le rendement à l'échéance.
En effet, la relation entre le prix de l'obligation et le taux
d'intérêt n'est pas linéaire mais convexe. Cette
convexité est toujours = 0 ; Cela induit que le cours de
l'obligation augmentera plus vite suite à la baisse de taux, qu'il ne
baissera suite à une hausse de taux de même ampleur. Cette
convexité est d'autant plus forte que la maturité de l'obligation
est élevée et que le taux du coupon est faible.
La convexité traduit concrètement la vitesse
avec laquelle le risque instantané d'une position ou d'un flux
évolue à mesure que les taux changent. Elle s'exprime comme la
dérivée seconde du prix par rapport au taux.
C'est une variation relative puisque la dérivée
est divisée par le prix initial :
Convexité = (1 / P) . (d2 P / d
r2)
Avec :
d2 P / d r2 = 1/(1+r)2 [
CF/(1+r)t (t2+t)]
La convexité se calcule simplement en utilisant la
formule suivante :
Convexité = (P+ + P-
-2P) / P* r2
Avec :
P+ le prix à la suite d'une variation de +1% (+100
points de base)
P- le prix à la suite d'une variation de -1% (-100
points de base)
P le prix initial.
| 


