II.II. THÉORIE DES VALEURS
EXTRÊMES ET VALUE-AT-RISK
V. Pareto s'intéresse à la fin du
XIXe siècle à la distribution des revenus dans la
société. Il en conclut que la société humaine est
fondée sur une loi mathématique de forme décroissante,
dans laquelle la distribution statistique prend une forme hyperbolique,
laissant apparaître des queues épaisses. Nous avons pu souligner
l'importance des lois issues de la famille
« parétienne », dont les applications en sciences
sociales sont croissantes au fil des années. L'abondante
littérature disponible sur le sujet en témoigne.
Le succès rencontré par ces lois nous a
incités à examiner leur apport sur le marché du DJIA en
période de crise des Subprimes. Cette application met en perspective
différents raisonnements en termes de rentabilité ajustée
du risque sur le marché des actions. La performance d'un investisseur
sur une période donnée est souvent liée à quelques
journées exceptionnelles. La distribution empirique de forme
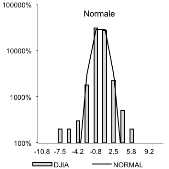
leptokurtique en témoignant (La grande majorité des cours se
concentre vers la moyenne historique proche de 0). La plupart des
journées d'activité ne contribue donc que marginalement au
résultat. Les activités de marché témoignent d'une
forte instabilité, révélant des mouvements violents et
soudains. C'est dans cet état statistique, où le nombre de
rentabilités anormales est important, que nous pouvons parler de crise.
La réalité erratique des cours de bourse est quantifiable. Nous
allons donner une image de cette réalité statistique dans un
premier temps avant de calculer notre loi de valeurs extrêmes.
II.II.1 ANALOGIE STATISTIQUE DE LA DISTRIBUTION DES RENDEMENTS
ET MAXIMUM DE VRAISEMBLANCE

Cette section a pour objet d'exposer la convergence des
variables standard issues de loi théorique de probabilité et
celles, empiriques, du DJIA pendant la période de test. Nous
déterminerons les hypothèses d'indépendance et
d'identité de la loi parente à partir de graphique logarithmique
permettant de comparer les variables entre elles. Lorsque la loi de valeurs
extrêmes est identifiée, les conditions de distribution
théorique peuvent être utilisées pour obtenir le type de
loi limite. Nous avons pu constater dans la section théorique que
certaines lois convergent vers différentes lois parentes. En effet, les
lois à support borné, comme la loi uniforme, appartiennent au
domaine d'attraction maximum de Weibull, avec   . Les lois
dont les queues décroissent de façon exponentielle appartiennent
au MDA de Gumbel, avec . Les lois
dont les queues décroissent de façon exponentielle appartiennent
au MDA de Gumbel, avec   Nous
pouvons citer à ce titre la loi normale et la loi exponentielle. Les
lois dont le paramètre de liberté est égal à Nous
pouvons citer à ce titre la loi normale et la loi exponentielle. Les
lois dont le paramètre de liberté est égal à   , faisant
apparaître des queues de distribution épaisses appartiennent,
comme la loi de student ou celle de Pareto, au MDA de Fréchet. Dans cet
exercice, nous avons choisi d'analyser quatre lois théoriques : , faisant
apparaître des queues de distribution épaisses appartiennent,
comme la loi de student ou celle de Pareto, au MDA de Fréchet. Dans cet
exercice, nous avons choisi d'analyser quatre lois théoriques :
§ La loi normale
§ La loi de Laplace
§ La loi de Pareto
§ La loi de student
II.II.1.1 ANALOGIE STATISTIQUE DE LA DISTRIBUTION DES
RENDEMENTS
GUMBEL

FRECHET
FRECHET


II.II.1.1.1 Comportement limite de
la loi exponentielle
La fonction de répartition de la loi exponentielle de
paramètre   est est  pour pour   . Avec . Avec   et et   , nous
pouvons résoudre l'équation donnée par le
théorème de Fisher-Tippet avec : , nous
pouvons résoudre l'équation donnée par le
théorème de Fisher-Tippet avec :

La loi de Laplace, ici représentée, et une loi
double exponentielle car sa densité peuvent être vue comme
l'association de deux lois exponentielles indépendantes, situées
de part et d'autre de la tendance centrale.
Le maximum normalisé et le MDA de la loi exponentielle
convergent vers une loi de Gumbel. C'est pour cette raison que la loi de Gumbel
est aussi appelée « loi de type
exponentiel ».
Prenons le théorème de Balkema-de
Haan-Picklands, en prenant   , où
u correspond au seuil défini. Alors : , où
u correspond au seuil défini. Alors :

Par conséquent, pour tout   , la GPD
s'accorde à être une loi exacte pour tout u pour le
paramètre , la GPD
s'accorde à être une loi exacte pour tout u pour le
paramètre 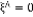  avec avec   . .
Nous pouvons constater une nette amélioration graphique
entre le DJIA et la loi de probabilité concernée. Nous retenons
donc la loi de Laplace pour cette raison.
| 


