I.2.3.5.1. LISSAGE DES SERIES
TEMPORELLES
Soient Y1, Y2 , Y3.....,
Yn un ensemble des nombres. on définit une moyenne
mobile d'ordre n que l'on obtient par la suite des moyennes
arithmétiques.
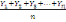 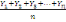 , ,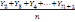 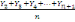 , ,  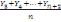 , (2) , (2)
Les sommes des numérateurs sont appelées totaux
mobiles d'ordre n.
Exemple : Soient les nombres 2, 6, 1, 5, 3, 7, 2
La moyenne mobile d'ordre 3 est obtenue comme suit
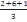 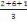 , , 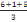 , ,  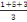 , , 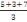 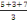 , , 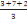 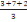 ou encore 3 ; 4 ; 3 ; 5 ; 4 ou encore 3 ; 4 ; 3 ; 5 ; 4
Dans une moyenne mobile, il est commode de localiser chaque
nombre à sa position relative par rapport aux données
d'origine.
Ainsi, dans cet exemple, on écrira :
Données d'origine 2,6, 1, 5, 3, 7, 2
Moyenne mobile d'ordre 3 3, 4, 3, 5, 4
Quand les données sont annuelles ou mensuelles, les
moyennes prennent respectivement les noms de moyennes mobiles sur n
années ou n mois. On parle ainsi de moyenne mobile sur 5 ans, de moyenne
mobile sur 12 mois, etc. Toute autre unité de temps peut être
utilisée.
Les moyennes de mouvement ont tendance à
« amortir » les variations entre les données. Ainsi,
dans le cas des séries temporelles, on utilise souvent cette
propriété pour éliminer des fluctuations
indésirables. Le processus est alors dénommé lissage des
séries temporelles.
Si on recourt aux moyennes arithmétiques
pondérées dans (2), les poids doivent être
spécifiés à l'avance, la suite obtenue sera appelée
moyenne pondérée d'ordre n.
Exemple : Supposons que dans l'exemple
précédent l'on prenne les poids 1, 4, 1. la suite serait
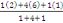  , , 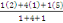  , ,  , , 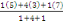  , , 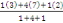 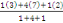
Ou 4, 5 ; 2, 5 ; 4 ; 5, 5 donne une moyenne de
mouvement pondéré d'ordre 3.
I.2.3.6. ESTIMATION DE LA
TENDANCE
La tendance peut être estimée de plusieurs
manières :
1.La méthode de moindres carrés vue
précédemment. Cette méthode permet de déterminer
l'équation de la droite ou de la courbe de tendance appropriée. A
partir de cette équation, on peut calculer les valeurs de T de la
tendance.
2. La méthode graphique, qui consiste à ajuster
une droite ou une courbe de tendance en se référant simplement
à son graphe, permet d'estimer T. cette méthode a
l'inconvénient d'être trop subjective.
3. La méthode de la moyenne mobile. Les moyennes
mobiles d'ordre approprié permettent d'éliminer les
modèles cycliques, saisonniers et accidentels et de ne conserver que
l'effet de la tendance. Un inconvénient de cette méthode est que
les données de début et de fin d'une série
sont « perdues ». Ainsi, dans le premier exemple, on
est parti d'un ensemble de 7 nombres, et au moyen d'une moyenne mobile d'ordre
3 on a obtenu 5 nombres. Un autre inconvénient est que les moyennes
mobiles peuvent engendrer des cycles ou d'autres mouvements qui
n'étaient pas présents dans les données d'origine. Enfin,
un troisième inconvénient est dû au fait que les moyennes
mobiles sont fortement affectées par les valeurs
« aberrantes » accidentelles.
4. La méthode des semi-moyennes consiste à
séparer les données en deux parties (de préférence
égale) et à faire la moyenne des données dans chaque
groupe.
On obtient ainsi deux points du graphique de la série
temporelle. On trace alors une droite de tendance entre ces deux points, ce qui
permet de déterminer les valeurs de la tendance. On peut aussi
déterminer les valeurs sans intermédiaire du graphique.
Bien que cette méthode soit simple à appliquer,
elle peut conduire à des résultats sans valeurs quand elle est
utilisée à tort et à travers. C'est pourquoi, bien qu'elle
soit valable dans le cas où les données peuvent être
classées en plusieurs groupes dans chacun desquels la
tendance est linéaire, elle n'est applicable que là
où la tendance est linéaire ou approximativement
linéaire.
| 


