3.3. DETERMINATION DE DECALAGE TEMPOREL PAR LE
CORRELOGRAMME
Figure 3-5 Correlogramme du taux de croissance
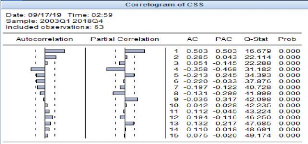
Source : Auteur (à l'aide d'eviews9)
Ce tableau montre que l'autocorrélation partielle pour
la variable CSS (taux de croissance du P113) présente 4 pics qui sortent
de l'intervalle. De ce fait, la variable sera retardée de 4
périodes (trimestres).
Figure 3-6 Correlogramme du taux Bon BCC
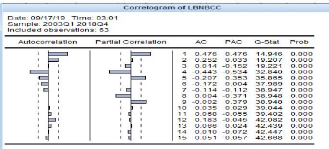
Source : Auteur (à l'aide d'eviews9)
~ 84 ~
Ce tableau montre que l'autocorrélation partielle pour
la variable LBNBCC (taux du Bon BCC) présente 5 pics qui sortent de
l'intervalle. De ce fait, la variable sera retardée de 5 périodes
(trimestres).
Figure 3-7 Correlogramme du niveau des
crédits
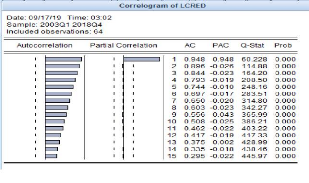
Source : Auteur (à l'aide d'eviews9)
Ce tableau montre que l'autocorrélation partielle pour
la variable LCRED (niveau de crédit accordé à
l'économie) présente 1 pic qui sort de l'intervalle. De ce fait,
la variable sera retardée d'une période (trimestres).
Figure 3-8 Correlogramme du coefficient de réserve
obligatoire
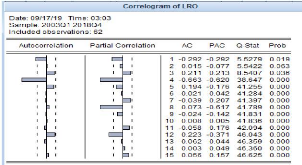
Source : Auteur (à l'aide d'eviews9)
Ce tableau montre que l'autocorrélation partielle pour
la variable LRO (coefficient de réserve obligatoire) présente 4
pics qui sortent de l'intervalle. De ce fait, la variable sera retardée
de 4 périodes (trimestres).
~ 85 ~
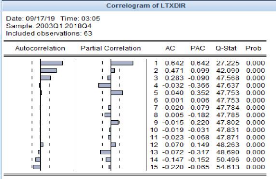
Figure 3-9 Correlogramme du taux directeur
Source : Auteur (à l'aide d'eviews9)
Ce tableau montre que l'autocorrélation partielle pour
la variable LTXDIR (taux directeur) présente 4 pics qui sortent de
l'intervalle. De ce fait, la variable sera retardée de 4 périodes
(trimestres, donc une année).
3.4. MODELISATION ARIMA
Il existe une catégorie de modèles qui cherche
à déterminer chaque valeur de la série en fonction des
valeurs qui la précède (yt = f(yt-1, yt-2, ...)). C'est le cas
des modèles ARIMA ("AutoRegressive - Integrated - Moving Average").
Cette catégorie de modèles a été popularisée
et formalisée par Box et Jenkins (1976).
Le choix d'un modèle est surtout théorique:
est-il raisonnable de penser que dans un phénomène donné,
les points sont fondamentalement fonction des points précédents
et de leurs erreurs, plutôt qu'un signal, périodique ou non,
entaché de bruit.
On peut noter cependant que souvent, on a recours à
l'analyse de variance pour traiter les séries temporelles. Or une des
assomptions majeures de l'ANOVA est que les résidus des
différentes mesures ne sont pas auto-corrélés. Ce n'est
évidemment pas le cas si la performance à l'essai t est
liée à la performance réalisée à l'essai
t-1.
Les processus autorégressifs supposent que chaque point
peut être prédit par la somme pondérée d'un ensemble
de points précédents, plus un terme aléatoire d'erreur.
Le processus d'intégration suppose que chaque point
présente une différence constante avec le point
précédent.
~ 86 ~
Les processus de moyenne mobile supposent que chaque point est
fonction des erreurs entachant les points précédents, plus sa
propre erreur.
Un modèle ARIMA est étiqueté comme
modèle ARIMA (p,d,q), dans lequel : p est le nombre de
termes autorégressifs, d est le nombre de
différences et q est le nombre de moyennes mobiles.
L'estimation des modèles ARIMA suppose que l'on
travaille sur une série stationnaire. Ceci signifie que la moyenne de la
série est constante dans le temps, ainsi que la variance. La meilleure
méthode pour éliminer toute tendance est de différencier,
c'est-à-dire de remplacer la série originale par la série
des différences adjacentes. Une série temporelle qui a besoin
d'être différenciée pour atteindre la stationnarité
est considérée comme une version intégrée d'une
série stationnaire (d'où le terme Integrated).
La correction d'une non-stationnarité en termes de
variance peut être réalisée par des transformations de type
logarithmique (si la variance croît avec le temps) ou à l'inverse
exponentielle. Ces transformations doivent être réalisées
avant la différenciation.
Une différenciation d'ordre 1 suppose que la
différence entre deux valeurs successives de y est constante.
yt - yt-1 = u + å t
u est la constante du modèle, et représente la
différence moyenne en y. Un tel modèle est un ARIMA (0,1,0). Il
peut être représenté comme un accroissement linéaire
en fonction du temps. Si u est égal à 0, la série est
stationnaire.
Les modèles autorégressifs supposent que yt est
une fonction linéaire des valeurs précédentes.
Littérairement, chaque observation est
constituée d'une composante aléatoire (choc aléatoire,
å) et d'une combinaison linéaire des observations
précédentes.
Les modèles à moyenne mobile suggèrent
que la série présente des fluctuations autour d'une valeur
moyenne. On considère alors que la meilleure estimation est
représentée par la moyenne pondérée d'un certain
nombre de valeurs antérieures (ce qui est le principe des
procédures de moyennes mobiles utilisées pour le lissage des
données). Ceci revient en fait à considérer que
l'estimation est égal à la moyenne vraie, auquel on ajoute une
somme pondérée des erreurs ayant entaché les valeurs
précédentes.
~ 87 ~
3.4.1. ESTIMATION DES MODELES
a. Estimation du premier modèle ARIMA
(1,3,4,5)
Dependent Variable: LCRED
Method: Least Squares
Date: 09/18/19 Time: 19:10
Sample (adjusted): 2004Q3 2018Q4
Included observations: 58 after adjustments
Variable
|
Coefficient
|
Std. Error t-Statistic
|
Prob.
|
LCRED(-1)
|
0.969759
|
0.007915 122.5248
|
0.0000
|
LRO
|
0.064200
|
0.151457 0.423886
|
0.6739
|
LRO(-1)
|
0.038525
|
0.155122 0.248349
|
0.8051
|
LRO(-2)
|
0.049927
|
0.155491 0.321091
|
0.7498
|
LRO(-3)
|
0.111981
|
0.153060 0.731613
|
0.4686
|
LRO(-4)
|
-0.473798
|
0.217329 -2.180092
|
0.0355
|
LTXDIR
|
0.007348
|
0.098880 0.074315
|
0.9411
|
LTXDIR(-1)
|
0.041441
|
0.103804 0.399224
|
0.6918
|
LTXDIR(-2)
|
0.011781
|
0.092516 0.127345
|
0.8993
|
LTXDIR(-3)
|
0.017942
|
0.091422 0.196256
|
0.8454
|
LTXDIR(-4)
|
-0.094294
|
0.084295 -1.118626
|
0.2698
|
LBNBCC
|
-0.022189
|
0.042752 -0.519007
|
0.6065
|
LBNBCC(-1)
|
-0.008759
|
0.044598 -0.196409
|
0.8453
|
LBNBCC(-2)
|
-0.002416
|
0.032204 -0.075018
|
0.9406
|
LBNBCC(-3)
|
-0.007857
|
0.031974 -0.245727
|
0.8071
|
LBNBCC(-4)
|
-0.022817
|
0.039158 -0.582687
|
0.5633
|
LBNBCC(-5)
|
-0.004697
|
0.028526 -0.164642
|
0.8700
|
C
|
0.485753
|
0.108984 4.457116
|
0.0001
|
R-squared
|
0.997350
|
Mean dependent var
|
13.77390
|
Adjusted R-squared
|
0.996315
|
S.D. dependent var
|
1.202687
|
S.E. of regression
|
0.073004
|
Akaike info criterion
|
-2.157277
|
Sum squared resid
|
0.218511
|
Schwarz criterion
|
-1.553354
|
Log likelihood
|
79.56102
|
Hannan-Quinn criter.
|
-1.922036
|
F-statistic
|
964.3118
|
Durbin-Watson stat
|
1.046272
|
Prob(F-statistic)
|
0.000000
|
|
|
|
La lecture des résultats de cette régression
mettant en relation le niveau de crédit à l'économie
(LCRED) par rapport à l'ensemble des variables exogènes (les
instruments de la politique monétaire de la BCC, à savoir le taux
directeur, le coefficient de réserve obligatoire et le taux du Bon BCC),
il ressort que la variable endogène (le niveau de crédit) est
expliquée à 99,63% par les variables explicatives ou
indépendantes (de la politique monétaire) du modèle.
Egalement, on remarque que globalement le modèle est significatif car la
valeur associée à la probabilité de Fisher (F-stat =
0,000000) est inférieure à 0,05.
b. Estimation du deuxième modèle ARIMA
(4,1)
Dependent Variable: CSS Method: Least Squares Date: 09/18/19
Time: 19:25
~ 88 ~
Sample (adjusted): 2004Q2 2018Q4
Included observations: 59 after adjustments
|
Variable
|
Coefficient
|
Std. Error t-Statistic
|
Prob.
|
|
CSS(-1)
|
0.395416
|
0.117629 3.361553
|
0.0014
|
|
CSS(-2)
|
0.162563
|
0.129116 1.259047
|
0.2135
|
|
CSS(-3)
|
0.081030
|
0.129056 0.627865
|
0.5328
|
|
CSS(-4)
|
-0.471223
|
0.117138 -4.022818
|
0.0002
|
|
LCRED
|
1.773005
|
0.929686 1.907100
|
0.0619
|
|
LCRED(-1)
|
-1.786379
|
0.934335 -1.911926
|
0.0613
|
|
R-squared
|
0.472306
|
Mean dependent var
|
-0.082855
|
|
Adjusted R-squared
|
0.422524
|
S.D. dependent var
|
0.751961
|
|
S.E. of regression
|
0.571429
|
Akaike info criterion
|
1.814793
|
|
Sum squared resid
|
17.30618
|
Schwarz criterion
|
2.026068
|
|
Log likelihood
|
-47.53639
|
Hannan-Quinn criter.
|
1.897266
|
|
Durbin-Watson stat
|
1.675371
|
|
|
La lecture des résultats de cette régression
mettant en relation le taux de croissance économique (LCSS) par rapport
à la variable exogène (le niveau de crédit accordé
à l'économie), il ressort que la variable endogène (la
variation du PIB) est expliquée à 42,25% par la variable
explicative ou indépendante (le niveau de crédit à
l'économie) du modèle. Egalement, on remarque que globalement le
modèle est significatif car la valeur associée à la
probabilité de Fisher (F-stat = 0,000000) est inférieure à
0,05.
| 


