II.4 Difficultés rencontrées
Les difficultés rencontrées sont : d'abord,les
difficultés liées à la réunion et la collecte des
données et l'intégration de celle-ci sur le cloud a partir de
l'outil d'en-treprise qui est Jira de façon automatique; ensuite, les
difficultés liées aux données (informations
erronées,inexactes,Données aberrantes,vides) ainsi qu'a la
transformation et l'anonymisation de certaines informations.
II.5 Décomposition du problème
Comme tout problème de machine learning celui-ci peut
être séparé en différent modules :
· Data pré-processing & intégration de
données.
· Application des modèles & optimisation
interprétation des résultats.
· et enfin post-processing &
présentation/visualisation
II.6 Data pre-processing
Cette étape consiste en l'extraction de
caractéristiques intéressantes des données et le nettoyage
de celle-ci.
II.6 Data pre-processing 25
PRévIsoN DE DATE DE PAssAGE DEs JALoNs 2022
En effet cette étape est importante dans
l'élaboration d'un projet de ML plus particulièrement pour
l'étape suivante qui consiste a appliquer les modèles,car le
modèle choisit est plus susceptible de retourner de meilleurs
résultat dans le cas ou les données sont bien
nettoyées.
II.6.1 Nettoyage des données
Cette étape consiste a éliminer toute les
informations que l'on ne souhaite pas conserver.
· informations erronées ,inexactes.
· informations vides ou non renseignés.
· informations redondantes
· informations sans intérêt pour l'analyse.
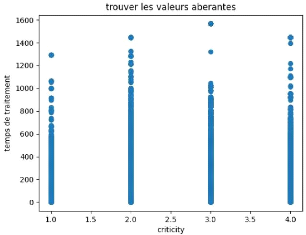
II.6.2 Chercher les valeurs aberrantes
L'un des moyens les plus efficace pour trouver les valeurs
aberrantes reste la visualisation.
En effet les valeurs qui sortent de l'ordinaire seront
facilement repérables.
26 CHAPITRE II. LE PROBLÈME
Amassin NACERDDINE Université Paris 8 Vincennes
FIG. 7 : Visualisation des valeurs aberrantes
II.6.3 Application des lois statistiques
Voir si les données obéissent a une certaine loi
de probabilité
· loi de poisson
· loi exponentielle
· loi normale
· loi de Zipf
· Loi de Benford
On peut utiliser ces lois pour éliminer les valeurs
peut représentatives au vu de leur faible probabilité.(STEwART
, 2000)
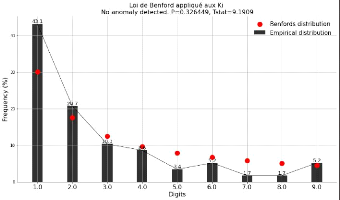
II.6.3.1 Loi de Benford
: Une série de nombres réels en écriture
décimale suit la loi de Benford si la fréquence d'apparition du
premier chiffre significatif c vaut approximativement pour
II.6 Data pre-processing 27
tout c entre 1 et 9 où log désigne le logarithme
décimal(BENFORD , 1938) fc = log(c + 1) -
log(c) = log(1 + 1 c)
PRéVISON DE DATE DE PASSAGE DES JALONS 2022
FIG. 8 : Loi de Benford appliquée aux Ki
Amassin NACERDDINE Université Paris 8
Vincennes
28 CHAPITRE II. LE PROBLÈME
| 


