III.9.6 MLP
Cette architecture consiste à organiser les neurones
en couches successives avec des interconnexion avec les couches adjacentes.Ou
chaque neurone est porteur d'une valeur comprise en générale
entre 0 et 1 (d'où une normalisation
préalable).
Comme pour les autres algorithmes supervisés on
cherche a optimiser la transformation f afin que pour les observations
xn d'un ensemble d'entraînement les
prédictions f(x) soit aussi proche que possible des valeurs
yn observées. pour se faire on ajuste durant la
phase d'apprentissage des poids wn qui sont associé
a chaque lien du réseau.(ROSENBLATT , 1958)
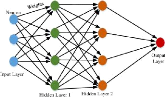
FIG. 18 : mlp
46 CHAPITRE III. TRAITEMENT
Amassin NACERDDINE Université Paris 8 Vincennes
Pour calculer la sortie du MLP en fonction des entrées
xn et des poids wn on procède
récursivement,couche par couche en combinant les deux opérations
d'addition et de multiplication passé a une fonction d'activation.
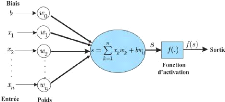
FIG. 19 : neurone-artificiel
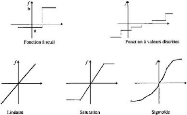
FIG. 20 : Fonctions d'activation les plus
utilisées
III.9 Les principaux algorithmes 47
PRévIsoN DE DATE DE PAssAGE DEs JALoNs 2022
III.9.6.1 rétropropagation
Pour expliquer le principe de rétropropagation on doit
comprendre le principe de l'erreur,la plus commune est l'erreur de la somme des
carrés des écarts.
E(w) = ?N n=1[f(xn; w) - Y n]2
Cette erreur E(w) s'exprime comme une somme de
contributions En(w) associé a chaque
observation(xn, yn).Ainsi pour trouver les
paramètres wn ou l'erreur E(w) atteint son
minimum,on calcule le gradient de ?En(w).
III.9.6.2 Initialisation judicieuse
Les expériences précédentes ont
montré qu'il est excrément utile d'initialiser judicieusement les
couches basses(la plus proche de l'entrée) pour améliorer les
performances d'un RN.
III.9.6.3 Utiliser le bon nombre de couches et de neurones
par couche
Les expériences précédentes en Deep
learning montrent qu'il est toujours intéressant d'avoir une couche
d'entrée qui a au moins la taille de vecteur d'entrer et les couches
suivantes qui représentent des puissances de deux.

| 


