Chapitre IV
Techniques d'évaluation
Sommaire
IV.1 Performance d'un modèle et sur-apprentissage
50
IV.2 Évaluation de la classification
51
IV.2.1 La matrice de confusion 51
IV.3 Évaluation de la régression
52
IV.3.1 RSS 52
IV.3.2 MSE 52
IV.3.3 RMSE 52
IV.3.4 RMSLE 52
Amassin NACERDDINE Université Paris 8 Vincennes
50 CHAPITRE IV. TRAITEMENT
IV.1 Performance d'un modèle et
sur-apprentissage
La performance d'un algorithmes de ML est bien entendu la
proportion de prédictions correctes(ou acceptable dans un certain sens)
faites sur le jeux de données utilisé pour
l'entraînement.
Néanmoins l'objectif du ML n'est pas de reproduire
avec une précision optimal les valeurs des variables cibles connues mais
bien de prédire les valeurs de celles qui n'ont pas encore
été observées et dont on ne connaît pas la
réponse.
En d'autres termes, il nous faut juger de la qualité
d'un algorithme de par sa capacité à généraliser
les associations apprises durant la phase d'entraînement à des
nouvelles observations.
IV.2 Évaluation de la classification 51
IV.2 Évaluation de la classification IV.2.1 La
matrice de confusion
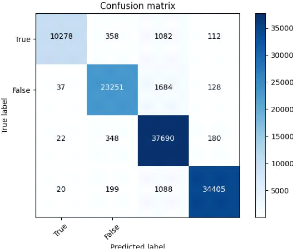
la matrice de confusion est une matrice qui mesure la
qualité d'un système de classification. Chaque ligne correspond
à une classe réelle et chaque colonne correspond à la
classe estimée.
La cellule ligne L, colonne C contient le nombre
d'éléments de la classe réelle L qui ont été
estimés comme appartenant à la classe C DBD , 2022
PRéVISON DE DATE DE PASSAGE DES JALONS 2022
FIG. 21 : Matrice de confusion
52 CHAPITRE IV. TRAITEMENT
Amassin NACERDDINE Université Paris 8 Vincennes
IV.3 Évaluation de la régression
Lorsque on parle d'évaluation de régression on
parle d'erreur, Celle-ci doit tendre vers 0.
IV.3.1 RSS
La somme des carrés des résidus, On calcule
pour chaque point xi du jeu de test la distance entre son
étiquette et la valeur prédite et en faire la somme.
RSS = ?n i=1(f(xi) -
yi)2
IV.3.2 MSE
Erreur quadratique moyenne, On garde les mêmes notion que
pour le RSS en
ajoutant la normalisation sur n nombre de points dans le jeu de
données.
?n
MSE = 1 i=1(f(xi) -
yi)2
n
IV.3.3 RMSE
Pour se ramener à l'unité de y , on peut prendre
la racine de la MSE. On obtient
v 1 ?n
ainsi la RMSE, ou Root Mean Squared Error. RMSE =
i=1(f(xi) - yi)2
n
IV.3.4 RMSLE
Le Root Mean Squared Log Errorr,pallie le problème des
étiquettes qui peuvent
prendre des valeurs qui s'étalent sur plusieurs ordres de
grandeur. v 1 ?n
RMSLE = i=1(log(f(xi) + 1) -
log(yi + 1))2
n
| 


