1.2 QUESTION DE RECHERCHE
La résolution de problèmes occupe une place
considérable dans les pratiques didactiques des mathématiques
à l'école élémentaire en France et bien dans
d'autres pays. C'est un moyen qui permet à l'apprenant la
dévolution aux problèmes, la manifestation des connaissances dans
ses interactions avec le milieu (Brousseau, 1998) et occupe un espace non moins
important dans les programmes (MEN, 2008) et le socle commun des connaissances
et des compétences (décret, 2006) en France. Cette
dévolution n'est possible qu'à travers des phases bien
déterminées indique
athéron (2011). Les travaux de l'Institut national de
recherche pédagogique, équipe de recherche en didactique des
mathématiques, menés dans le sens de susciter des apprentissages
par la résolution de problèmes, définissent à
travers le manuel « apprentissages numériques et résolution
de problèmes » les objectifs de chaque contenu et les phases de
résolution de problèmes subdivisée en étapes
successives.
Dans notre recherche, tout en nous inscrivant dans un champ
comparatiste existant de l'agir ensemble (Assude T. & Mercier,A. 2007),
nous voulons comprendre en quoi le milieu de résolution de
problème est un lieu de production de techniques variées ?
1.3 HYPOTHESE DE LA RECHERCHE
Notre cadre théorique suffisamment édifiant sur
les techniques qu'utilise l'homo-sapiens quelle que soit la tâche
à laquelle il se confronte, nous amène à penser que les
élèves vont utiliser dans la conduite de leur topos des
manières de faire en s'appuyant sur les ostensifs , les non ostensifs et
la mémoire pour expliquer les opérations.
2. Méthodologie
2.1 CONTEXTE DE LA RECHERCHE
Ce travail de recherche est certes produit aux fins
d'obtention d'un master 2 de recherche mais il s'inscrit
précisément dans un champ d'actions dont l'articulation se fait
autour du savoir-faire de l'apprenant lors d'une rencontre avec le savoir que
lui propose l'enseignant. Un intérêt qui pourrait nous conduire
à étendre notre observation au plus grand nombre. Nous avons
plutôt choisi de travailler dans une classe d'une école primaire
d'AIX-Marseille composée de CM1 et CM2 où les
élèves sont supposés avoir accumulés des
réflexes de raison. Cette classe, dont les effectifs de CM1 et CM2
étaient de 10 et 13, est un milieu de résolution de situation
problème en mathématique et surtout qu'elle a l'habitude de la
présence de la caméra et/ou des personnes
étrangères.
13
2.2 RECUEIL DES DONNEES : TRANSCRIPTION ET
COPIES
Deux séances composées de quatre tâches du
même type peuvent suffire pour offrir au chercheur la possibilité
de collecter des données nécessaires à l'analyse. La
première tâche que nous pouvons qualifier de moyen de
révélation des techniques empruntes d'originalité ; parce
que produite sans référence à une technique d'emploi dans
la classe. A partir de la deuxième tâche, il peut avoir des
influences langagières qui modifient de façon significative les
pratiques des élèves, donc il y a la possibilité de voir
un élève utiliser une technique déjà
utilisée par un autre élève de la classe. Pour ce faire
nous transcrirons l'oral de la leçon afin d'avoir la matière de
structuration du synopsis, mais plus le champ de la recherche pratique
présentant divers aspects des discours possibles. Nous exploiterons
également à côté des transcriptions, les copies des
élèves. Nous utilisons la méthode quantitative en raison
de son principe qui veut que les hypothèses soient testées lors
du travail de collecte de données à travers l'emploi
d'instruments ou de documents qui permettent une vérification
quantifiable.
2.3 LA TRANSCRIPTION : UNE RAISON DES SEANCES
FILMEES.
Les séances filmées ont la tendance de
présenter une diversité de phénomènes non
perceptible à une simple observation faite en une fois. Le film a un
attribut avéré de reprise du défilé d'actions
produites par les acteurs de la scène. Le film nous permet de structurer
le synopsis (le déroulement des opérations de l'enseignant et
celles des élèves le dosage à travers les phases ou
tâches du même type) grâce à un moment fastidieux mais
riche de transcription et donc de voir les interventions des
élèves dans l'action conjointe du professeur et des
élèves afin d'établir une analyse possible. Il peut donc
permettre de voir certains écrits des élèves d'enregistrer
les justifications orales (logos) de ce que les élèves utilisent
comme moyen (technique) pour arriver à la réponse attendue.
14
2.4 L'ENREGISTREMENT DE LA LEÇON
Tableau
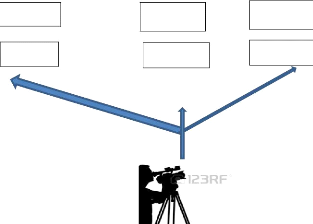
Table 1
Table 4
Table 2
Table 5
Table 3
Table 6
Illustration 2 : Plan du dispositif d'enregistrement
vidéofilmé des données
Nous avons utilisé deux caméras en affectant
à chacune d'elles une mission bien précise :
Une caméra comme présentée dans le
schéma ci-avant qui est une caméra posée sur l'axe
centrale de la classe. Elle nous permet d'enregistrer toutes les actions
produites ensemble dans les communications du groupe classe. Elle nous montre
particulièrement comment l'enseignant définit les tâches de
travail les dévolue les régule ou les institutionnalise. Elle
permet certes de voir les justifications des élèves mais aussi de
voir les interactions entre le professeur- élèves et entre les
élèves.
Une autre caméra portable gardée dans la main du
chercheur permet de filmer toutes actions individuelles de l'apprenant. Il
s'agira à ce niveau de prendre ce qu'écrit chaque
élève,
2.5 LA COPIE DE L'ELEVE : UNE TRACE
D'OBSERVATION.
Pour observer comment les élèves de ces deux
niveaux, mis ensemble, réagissent pour fournir l'attendu de l'enseignant
qui les dévolue à quelques tâches définies dans le
manuel scolaire « Apprentissages numériques et résolution de
problèmes. » dont chacune intègre la question ci pertinente
de la recherche de trois nombres qui se suivent dont la somme d'avance
fixée. Les copies des élèves sont
toutes aussi importantes que le film, car elles offrent au
chercheur le déroulement des opérations qui devra se montrer
comme un mouvement continu d'étapes intelligibles ou plutôt comme
un mouvement entrecoupé de marques de reprise susceptibles d'amener
à la réponse.
2.6 ANALYSE A PRIORI
Avant de regarder au détail, les productions des
élèves à partir d'un problème il nous semble
important d'établir une certaine compréhension autour :
? du savoir choisi contenu dans une ressource d' Hatier ER EL C
1
? des praxéologies possibles de l'instance apprenant
? des problèmes didactiques que peut rencontrer
l'enseignant dans le cadre du déroulement de ce savoir.
2.6.1 Présentation et analyse a priori du
savoir 2.6.1.1 Présentation
Ce savoir mathématique a été
modélisé par l'Equipe de recherche en didactique des
mathématiques à l'Institut national de recherche
pédagogique et prescrit dans la collection d' Hatier 6ERMEL
dont le titre est « apprentissage numériques et résolution
de problèmes CM1 cycle 3. » (2005, p.62-66).Dans ce manuel
l'articulation de l'apprentissage se fait en trois phases
découpées en deux étapes chacune.
Le type de tâche est défini tel que le
maître doit prendre un exemple au début pour expliquer en quoi
consiste le problème. « Les nombres 5,6 et 7 sont trois nombres qui
se suivent et leur somme est 18. Je vais vous donner un nombre qui va
être la somme de trois nombres qui se suivent et vous, vous allez
chercher ces trois nombres. » :
Première phase : appropriation du problème et
premières recherches
1ère étape : recherche pour s=96. Consigne :
« vous allez chercher trois nombres qui se suivent dont la somme est 96.
Ecrivez tous les calculs que vous faites, il faudra ensuite expliquer comment
vous avez trouvé. ».
2ème étape : On fait avec un nombre plus grand ;
s=354
15
6 ERMEL : Equipe de Recherche sur les athématiques dans
l'Enseignement Elémentaire.
16
Deuxième phase : expliciter les propriétés
qui permettent de prouver
1ère étape : recherche individuelle avec s=25 et
s=45.l'objectif est de faire découvrir qu'il n'est pas toujours possible
de trouver trois nombres qui se suivent correspondant à une somme
donnée.
2ème étape : attendre des élèves
une formulation des propositions apportant la preuve que c'est impossible avec
s=25
2.6.1.2 Analyse a priori du savoir
Il s'agissait d'un cas de problème pouvant être
assimilé aux équations du premier degré à une
inconnue de la forme de : trouver x s'il existe tel que ( x -- 1) + x + (x
+ 1) = n (avec n E N) ou x + (x + 1) + (x + 2) = n (avec n E N) ;
car si l'on considère x + (x + 1) + (x + 2) = n, on a : n =
3x + 3 = 3(x + 1) . Dans cette forme,
on sait que n est multiple de 3. Donc après la
division de a , (x + 1) est
considéré
comme deuxième terme successif. Le premier
naturellement étant x si on introduit -1 à (x + 1)
et le troisième en ajoutant + 1 sur (x + 1). L'idée
de trois nombres qui se suivent est bien du domaine d'une suite de raison r = 1
; ce qui peut bien sûr faire l'objet d'un apprentissage ou qui apporte le
problème aux apprenants des niveaux de CM1 et CM2. La raison r est la
condition de résolution à un degré superieur que demander
simplement de trouver trois nombres identiques dont la somme se trouve
être n multiple de 3 ou n= 3. x . Il y a un
réel besoin de communication qui peut se produire entre
l'arithmétique et l'algèbre. Chacun prenant appui sur l'autre
pour expliquer le schéma de la résolution.
2.6.1.3 Analyse a priori des praxéologies de
l'instance apprenant
Nous savons que les tâches ou les types de tâches
provoquent généralement chez l'homo-sapiens, des manières
de faire qui sont parfois les mêmes. Le début du jeu est un moment
nous semble-t-il tout indiqué pour voir à quoi
l'élève va-t-il s'en tenir. Ainsi nous imaginons des techniques
possibles(T) que pourraient dérouler les élèves
de la classe choisie devant le problème présenté sous la
façon suivante : trouvez trois nombres qui se suivent dont la somme
(n) est donnée.
1 : multiplication d'un nombre x E N (pris au hasard)
par 3 et voir si le produit donne . Puis considérer qu'ils sont trois
nombres identiques et faire -- 1 pour le plus petit et x + 1 pour le
plus grand.
T2 : décomposition du chiffre des dizaines et
celui des unités pour trouver les trois nombres dont le nombre somme est
96. On a : 9 = 3+3+3 et 6= 3+2+1 pour le résultat suivant 31-32-33 ou
décomposition des dizaines et essai d'unités. On a 96= 90+6 et
on
17
écrit 90 = 30+30+30 ensuite à chaque 30, on y
met un chiffre à la place de 0 et on voit si les trois chiffres
constituent la suite dont le total est 6.
T3 : division du nombre somme ( n) par 3
pour trouver le deuxième nombre dans cette suite. Et successivement, on
retranche 1sur le deuxième pour trouver le premier et on ajouter 1 au
deuxième pour obtenir le troisième.
T4 : Technique intuitive. Elle relève des
opérations mentales ne donnant pas l'occasion à l'enseignant de
voir quelle est la procédure de résolution utilisée. Sur
la feuille, on voit juste les trois nombres qui se suivent dont la somme est
effectivement celle que l'enseignant a donnée. Cette technique peut
être rangée parmi les techniques invisibles si
l'élève ne l'explicite pas pour qu'une trace écrite nous
situe.
T5 : tirage d'une suite quelconque au sein des
entiers naturels et vérification de la proximité de leur somme
à la somme donnée : il s'agit d'opérer dans un intervalle
possible. 96 est la somme de trois nombres qui se suivent de deux chiffres et
non un ou trois chiffres.
T6 : retrait du surplus des deux plus grands nombres
du nombre somme, ensuite division par 3 pour obtenir le plus petit et ajouter
successivement + 1 et +2 au plus petit. On a 96-3=93, puis 93/3=31
et 31+1=32 ; 31+2=33.
2.6.2 Des résurgences des positions diverses des
élèves avec
Certains élèves qui pensent que ça marche
avec tous les nombres, vont prendre du recul en se posant la question s»il
n'y a pas des cas pour lesquels ça marche bien et d'autres pour lesquels
ça ne marche pas.
Des élèves qui pensent que ça marche
toujours pour vue qu'on accepte les nombres décimaux
Des élèves qui trouvent des nombres très
proches dont la somme n ne vérifie pas le nombre donné.
Exemple 25, ils peuvent trouver 7-8-9 avec n= 24 et 8-9-10 avec
n= 27. Mais pour n =25, la solution n'existe pas !
2.6.3 Marche vers une conjecture
La condition d'existence indiquée ci-haut de x
qui existe tel que (x -- 1) + x + (x + 1) = n (avec n E N) est
« n doit être multiple de 3 ». C'est pourquoi, il
importe d'introduire deux cas de figure pour provoquer des interrogations
à vocation ascendante dans leurs manières de faire :
18
n multiple de 3 ; c'est-à-dire n = 3(x + 1) et savoir
s'il existe une solution car x existe. Exemple n =12 ; on sait que 12=3x4 ou
12= 3x (3+1). On peut utiliser les tables de multiplication ou la calculatrice
pour vérifier 3x4 = ?
n non multiple de 3 ; c'est-à-dire n # 3(x + 1) et
savoir s'il y a une solution car x n'existe pas. Exemple n =13 ; on sait que
13? 3 x un nombre entier. On peut utiliser les tables de multiplication et/ou
la calculatrice pour vérifier qu'il n'existe aucun entier naturel qui
soit multiplié par 3 pour obtenir 13.
2.6.4 Analyse a priori des problèmes didactiques
possibles
Organiser le jeu pour mettre en action l'élève
est ce qui explique la présence du professeur à l'école.
Nous savons que les deux acteurs ont une histoire construite en classe autour
des premiers savoirs donnés qui servent de point d'appui à la
construction d'une nouvelle histoire. La modélisation
réalisée sur le problème par l'équipe de recherche
en mathématique a certes donné une forme accessible au savoir
mais il reste à l'enseignant le pouvoir de réalisation. Dans le
contrat didactique le professeur attend une réponse produite par l'usage
d'une technique qui produit un intérêt à notre recherche.
Si l'enseignant parvient à établir la compréhension
suffisante du problème de recherche aux élèves nous
pouvons penser qu'il s'appuiera sur les prés requis ou les acquis des
élèves qui sont divers ; par exemple sur la maîtrise de la
division euclidienne la multiplication les caractères de
divisibilité d'un nombre par 3 ou les caractères de nombre
multiple de 3.
Bien que l'enseignant sache compter sur les
élèves mais il ignore les représentations réelles
de ces derniers vis-à-vis du problème présenté.
C'est pourquoi il peut s'agir de voir l'enseignant définir
réguler et dévoluer la première tâche : ce que lui
impose l'action didactique conjointe du professeur-élève.
19
2.7 SYNOPSIS DE SEANCES
|
Séance
|
Temps en
minutes
|
Nombre de
tours de parole
|
Organisation : Faire jouer le jeu
|
Jeu : étapes de
l'activité
|
Observations
|
|
1. (á)
|
0mn
6mn
|
Professeur : 11 Elèves : 9
|
? L'Enseignant définit et dévolue le type de
tâche et la tâche1 aux élèves.
? L'écoute
individuelle des élèves
|
Type de tâche (T) :
trouver trois
nombres qui se
suivent dont la
somme est donnée !
Exemple : somme
= 18 ; les trois
nombres sont 5 ; 6 et 7.
t1 : trouver trois
nombres qui se
suivent dont le total est 96
|
Réactions de
compréhension
|
|
0mn
27,5mn
|
Professeur : 24 Elèves : 23
|
Travail individuel
|
Résolution du
problème :
Les élèves résolvent le problème
chacun avec une technique. correction
|
|
20
1.(â )
|
28mn53s
|
professeu r :
élèves :
|
· Rappel des techniques utilisées à la
séance 1.a distribution feuilles vierges.
|
t 2 :
· trouver trois nombres qui se suivent dont la somme
connue est un grand nombre ; 354
|
|
|
|
|
Résolution du
problème : les élèves résolvent le
problème chacun en maintenant sa technique ou en utilisant une technique
présentée par un autre élève lors des
justifications à la séance 1.a
|
Production de la réponse au moyen des techniques
invisibles et faibles
|
|
|
complément ou approfondis sement
|
1.â
· 00mn
5mn
|
Professeur : 63
|
Rappel du jeu sur les trois nombres qui se suivent et des
techniques.
|
t 3
trouver trois nombres qui se
suivent pour sept sommes
connues (324 ; 645 ; 915 ; 144 ; 273
; 489 et 552)
· un nouveau nombre
724 pour les élèves
qui ont fini.
|
|
|
|
|
· Résolution du problème : les
élèves résolvent le problème chacun en
|
|
|
21
10mn
22mn02s
|
Elèves : 34
|
avec tableau à 4
entrées et lignes
pour explications.
· Travail individuel
des élèves.
|
maintenant sa technique ou en utilisant une technique
présentée par un autre élèves
· Les élèves qui travaillent sur 724
indiquent un reste de 1 ou le nombre moyen est décimal
|
|
|
|
|
|
|
· Travail individuel et
|
|
|
|
32mn12
|
|
Ramassage des feuilles ; pas de correction au tableau
|
|
|
|
00mn
|
|
· Rappel du
caractère de
|
t4 :
|
Réactions positives
|
|
|
|
nombre divisible
|
· trouver trois nombres
|
:
|
Séance 2
|
4mn11 s
|
|
par 3 et des
techniques utilisées
|
qui se suivent pour sept
sommes connues (141 ;
|
impossib ilité ;
|
|
|
|
lors de la séance 1.a
|
309 ; 251 ; 624 ; 563 ;
|
reste 1 et
|
|
|
|
prolongée en 1.b et
|
701 et 414)
|
ne sont
|
|
|
17mn12s
|
Prof : 101
|
approfondissement
|
· Deux nouvelles sommes pour les élèves qui
ont fini
|
pas
divisible
|
|
|
|
Distribution de
|
(525 et 421)
|
|
|
19mn05s
|
Elèves : 73
|
feuilles récupérées
à la fin
· Régulation
|
· Extension avec cinq
nombres dont la somme est 525,
quatre nombres dont la somme est
|
s par 3
|
|
|
|
|
324 et sept nombres dont la somme est
|
|
|
|
|
|
1267
|
|
|
33mn45s- 51mn30
|
|
· Travail individuel des élèves.
|
Résolution de problèmes et discussion pour 324
|
|
|
|
récréation
|
|
|
|
Correction.
|
|
|
|
|
0mn-4mn45
|
|
|
|
|
22
2.8 LE JEU ET SA DEVOLUTION
Le recueil de données qui s'est fait en dates du 28mars
et du 02 avril 2013 et qui portait sur le travail des élèves
à travers les tâches (t1- t2- t 3- t4) susmentionnées dans
le tableau synoptique ci-dessus, présente quelques aspects y
résumés. Au début de la tâche (t1) l'enseignant dans
l'esprit de la présentation du savoir tel qu'indiqué dans la
ressource exploitée, définit le type de tâche (T) en
prenant un exemple avec le petit nombre somme 18. Le professeur (y) effectue la
somme de 5 ; 6 et 7 pour montrer deux choses :
- Que la somme est 18
- Que les trois nombres se suivent.
Cet exemple choisi est un moyen de dévolution des
élèves au problème et d'adaptation que le professeur (y)
met en action dans son topos pour faire comprendre la règle du jeu qui
est de trouver trois nombres qui se suivent dont la somme (multiple ou non
multiple de 3) est donnée. Des comportements de recherche de
compréhension se manifestent par des questions pertinentes des
élèves. L'enseignant qui compte sur les ressources individuelles
des élèves leur donne l'occasion de travailler seul. Cette
façon permet à chaque apprenant de générer des
éléments de technique personnelle. C'est un travail qui se fait
entre d'importants moments des séances. Pour la tâche (t1) on
observe 27mn 30s d'activité accordées aux élèves
dont l'attendu de l'enseignant est la réponse au problème
posé. Pour la tâche (t2), on a 6mn45s ; la tâche (t3),
12mn02s et la tâche (t4) ,17mn45s. On voit bien que les
élèves ont pris assez de temps lors de leur premier contact avec
le savoir.
S'il est vrai que le travail individuel pour le chercheur
permet de voir ce qu'utilise chaque acteur ( i) comme technique dans ce jeu, il
est aussi vrai que la mise au net ou correction lui permet de voir les causes
des changements des techniques par certains élèves ( 1 ... 23)
lors d'une autre tâche.
23
| 


