1.1.2 .... À la formulation générale
des modèles à équations simultanées
La forme structurelle du modèle à équations
simultanées, dans le cas général, s'écrit comme
suit :

+ +...+ + + +... + =
+ +...+ + + +... + =
Page | 69
...

+ +...+ + + +... + =
Ce modèle renferme M équations et M variables
endogènes ( , , ..., ). Il comporte k
variables exogènes ( , ,..., ) pouvant également
contenir des valeurs prédéterminées
des variables endogènes. Il importe de signaler que l'une
des variables peut être munie de 1 en
vue de tenir compte du terme constant dans chacune des
équations. Les termes d'erreur ( ,
, ..., ) sont dénommés perturbations
structurelles.
B =
; Y=
; X=
?3t

...
...
...

; I' =
...
...
...

Ce modèle peut encore s'écrire sous forme
matricielle de la manière suivante : BY + I'X = E
;E =
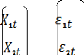
Page | 70
Chacune des équations contient une des variables
endogènes ayant un coefficient égal à 1 : c'est
précisément la variable dépendante. Ce qui signifie que
dans la matrice B, chacune des colonnes renferme au moins une valeur
égale à 1. Il s'agit de la normalisation. Par
contre, les équations dans lesquelles tous les coefficients sont
égaux à 1 et dépourvues de perturbations sont les
équations d'équilibre.
Au cas où la matrice B est non
singulière63, elle est inversible et la forme réduite
du modèle peut être dérivée rendant possible
d'exprimer la matrice Y en fonction de la matrice X :
Y = -B-1 X
+ B-1å
Il convient de rappeler que la forme réduite permet
d'exprimer chaque variable endogène en fonction des variables
exogènes ou prédéterminées et des perturbations. Il
importe aussi de noter que les équations de la forme réduite
peuvent être estimées par les MCO, car les variables
endogènes sont supposées non corrélées avec les
termes d'erreur. Après avoir estimé les paramètres des
équations de forme réduite, il est susceptible de
déterminer les paramètres des équations structurelles en
utilisant la méthode des moindres carrés
indirects.
Le passage de la forme structurelle n'est pas aisé dans
la pratique comme il en est en théorie. En effet, le fait de connaitre
les éléments de la matrice ( B-1 ) dans la forme
réduite ne permet pas de déterminer c'est-à-dire
d'identifier les matrices B et séparément. On détient un
système de (M × k) équations à (M × M) + (M
× k) inconnues qui ne peut être résolu sans certaines
restrictions : C'est ce qu'on appelle le problème de
l'identification.
| 


